数据结构 -- 二叉树&二叉搜索树
二叉树
二叉树是这么一种树状结构:每个节点最多有两个孩子,左孩子和右孩子
重要的二叉树结构
-
完全二叉树(complete binary tree)是一种二叉树结构,除最后一层以外,每一层都必须填满,填充时要遵从先左后右
-
平衡二叉树(balance binary tree)是一种二叉树结构,其中每个节点的左右子树高度相差不超过 1
1) 存储
存储方式分为两种
-
定义树节点与左、右孩子引用(TreeNode)
-
使用数组,前面讲堆时用过,若以 0 作为树的根,索引可以通过如下方式计算
-
父 = floor((子 - 1) / 2)
-
左孩子 = 父 * 2 + 1
-
右孩子 = 父 * 2 + 2
-
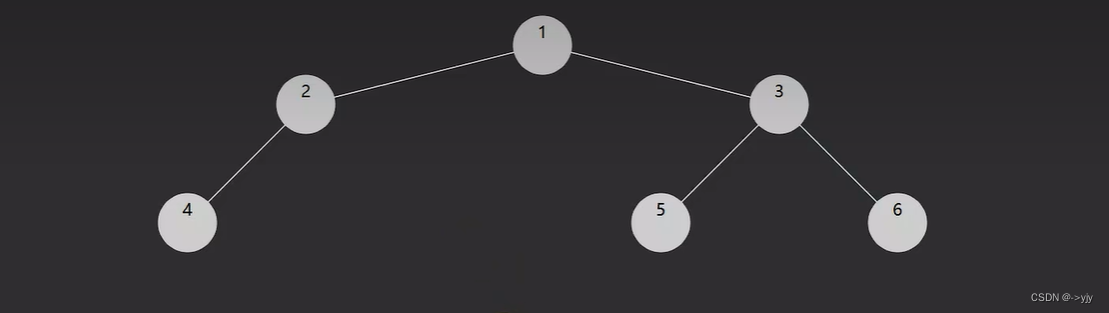
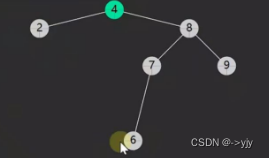
没有孩子的节点也有一个称呼:叶子结点
我们之前学优先级队列和堆结构的时候其实都接触过,比如我们之前学的大顶堆
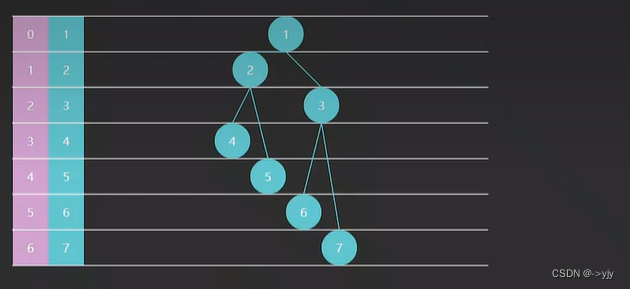
当然大顶堆这种二叉树属于比较特殊的二叉树,叫完全二叉树,也就是除了最后一层以外,每一层都得填满而且填充的顺序必须从左到右填充
遍历
遍历也分为两种
1.广度优先遍历(Breadth-first-order):尽可能先访问离根最近的节点,也称为层序遍历
2.深度优先遍历(Depth-first-order):对于二叉树,可以进一步分为三种
1.pre-order前序遍历,对于一棵子树,先访问该节点,然后是左子树,最后是右子树
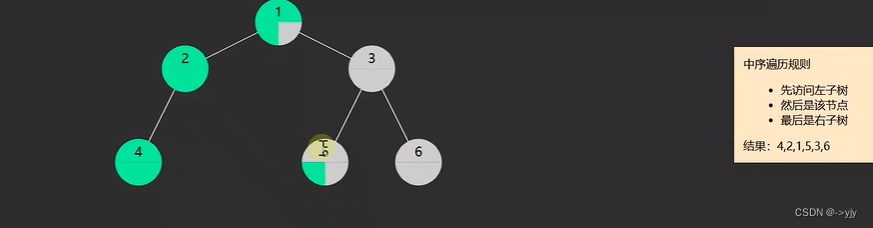
2.in-order中序遍历,对于每一颗子树,先访问左子树,然后是该节点,最后是右子树
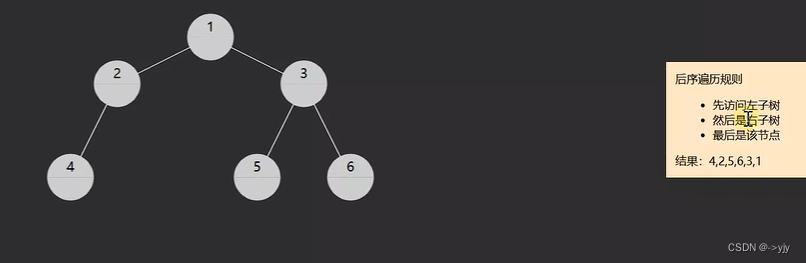
3.post-order后序遍历,对于每一棵子树,先访问左子树,然后是右子树,最后是该节点

| 本轮开始时队列 | 本轮访问节点 |
|---|---|
| [1] | 1 |
| [2, 3] | 2 |
| [3, 4] | 3 |
| [4, 5, 6] | 4 |
| [5, 6] | 5 |
| [6, 7, 8] | 6 |
| [7, 8] | 7 |
| [8] | 8 |
| [] |
-
初始化,将根节点加入队列
-
循环处理队列中每个节点,直至队列为空
-
每次循环内处理节点后,将它的孩子节点(即下一层的节点)加入队列
注意
以上用队列来层序遍历是针对 TreeNode 这种方式表示的二叉树
对于数组表现的二叉树,则直接遍历数组即可,自然为层序遍历的顺序
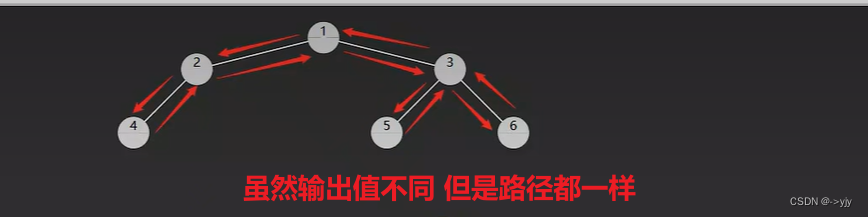
深度优先
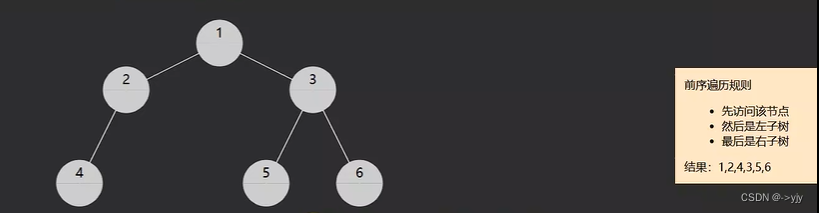
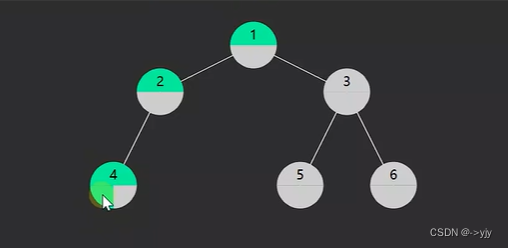
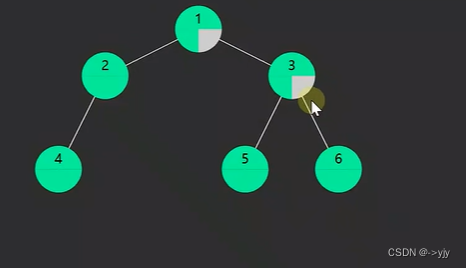
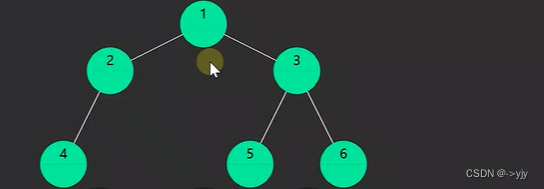
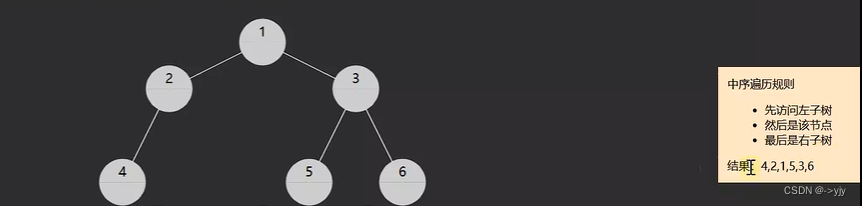
递归
public class TreeTraversal {
public static void main(String[] args) {
/*
1
/ \
2 3
/ /\
4 5 6
*/
TreeNode root = new TreeNode(
new TreeNode(new TreeNode(4),2,null),
1,
new TreeNode(new TreeNode(5),3,new TreeNode(6))
);
preOrder(root);//124356
System.out.println();
inOrder(root);//421536
System.out.println();
PostOrder(root);
System.out.println();
}
/**
* 前序遍历
* @Params:node-节点
*/
static void preOrder(TreeNode node){
if(node==null){
return;
}
System.out.print(node.val+"\t");//当前节点值
preOrder(node.left);// 左
preOrder(node.right);// 右
}
/**
* 中序遍历
* @Params:node-节点
*/
static void inOrder(TreeNode node){
if(node==null){
return;
}
inOrder(node.left); //左
System.out.print(node.val+"\t");//值
inOrder(node.right);//右
}
/**
* 后序遍历
* @Params:node-节点
*/
static void PostOrder(TreeNode node){
if(node==null){
return;
}
PostOrder(node.left);
PostOrder(node.right);
System.out.print(node.val+"\t");
}
}
非递归
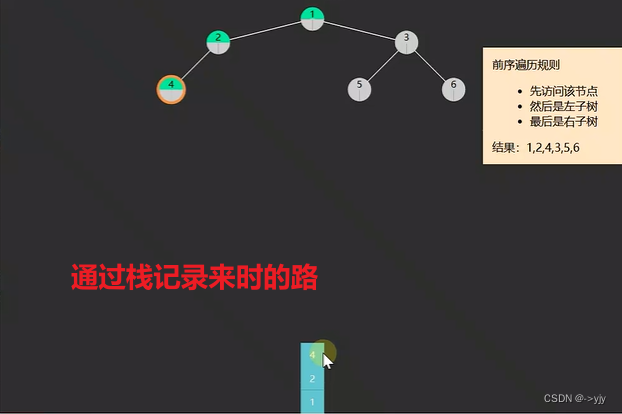
非递归实现
前序遍历 这里的LinkedListStack是自己实现的 也可以用Java自带的LInkedList
LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
while (!stack.isEmpty() || curr != null) {
if (curr != null) {
stack.push(curr);
System.out.println(curr);
curr = curr.left;
} else {
TreeNode pop = stack.pop();
curr = pop.right;
}
}中序遍历
LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
while (!stack.isEmpty() || curr != null) {
if (curr != null) {
stack.push(curr);
curr = curr.left;
} else {
TreeNode pop = stack.pop();
System.out.println(pop);
curr = pop.right;
}
}后序遍历
LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
TreeNode pop = null;
while (!stack.isEmpty() || curr != null) {
if (curr != null) {
stack.push(curr);
curr = curr.left;
} else {
TreeNode peek = stack.peek();
if (peek.right == null || peek.right == pop) {
pop = stack.pop();
System.out.println(pop);
} else {
curr = peek.right;
}
}
}对于后序遍历,向回走时,需要处理完右子树才能 pop 出栈。如何知道右子树处理完成呢?
-
如果栈顶元素的 right==null 表示没啥可处理的,可以出栈
-
如果栈顶元素的right!=null,
-
那么使用 lastPop 记录最近出栈的节点,即表示从这个节点向回走
-
如果栈顶元素的 right==lastPop 此时应当出栈
-
对于前、中两种遍历,实际以上代码从右子树向回走时,并未走完全程(stack 提前出栈了)后序遍历以上代码是走完全程了
统一写法
下面是一种统一的写法,依据后序遍历修改
LinkedList<TreeNode> stack = new LinkedList<>();
TreeNode curr = root; // 代表当前节点
TreeNode pop = null; // 最近一次弹栈的元素
while (curr != null || !stack.isEmpty()) {
if (curr != null) {
colorPrintln("前: " + curr.val, 31);
stack.push(curr); // 压入栈,为了记住回来的路
curr = curr.left;
} else {
TreeNode peek = stack.peek();
// 右子树可以不处理, 对中序来说, 要在右子树处理之前打印
if (peek.right == null) {
colorPrintln("中: " + peek.val, 36);
pop = stack.pop();
colorPrintln("后: " + pop.val, 34);
}
// 右子树处理完成, 对中序来说, 无需打印
else if (peek.right == pop) {
pop = stack.pop();
colorPrintln("后: " + pop.val, 34);
}
// 右子树待处理, 对中序来说, 要在右子树处理之前打印
else {
colorPrintln("中: " + peek.val, 36);
curr = peek.right;
}
}
}
public static void colorPrintln(String origin, int color) {
System.out.printf("\033[%dm%s\033[0m%n", color, origin);
}
将回的代码注释掉那就是一个前序遍历代码
将去的代码注释掉那就是一个中序遍历代码
练习

代码实现:
public class E04Leetcode101 {
public boolean isSymmetric(TreeNode root){
return check(root.left,root.right);
}
private boolean check(TreeNode left, TreeNode right) {
if(left==null&&right==null){
return true;
}
//执行到这里说明:left 和 right不能同时为null
if(right==null||left==null){
return false;
}
if(left.val!=right.val){
return false;
}
return check(left.left,right.right) && check(left.right,right.left);
}
}
测试类:
import org.junit.Test;
import static org.junit.Assert.assertTrue;
public class TestE04Leetcode101 {
@Test
public void test1(){
TreeNode root = new TreeNode(
new TreeNode(new TreeNode(3),2,new TreeNode(4)),
1,
new TreeNode(new TreeNode(4),2,new TreeNode(3))
);
assertTrue(new E04Leetcode101().isSymmetric(root));
}
@Test
public void test2(){
TreeNode root = new TreeNode(
new TreeNode(null,2,new TreeNode(3)),
1,
new TreeNode(null,2,new TreeNode(3))
);
assertTrue(new E04Leetcode101().isSymmetric(root));
}
}

分析:
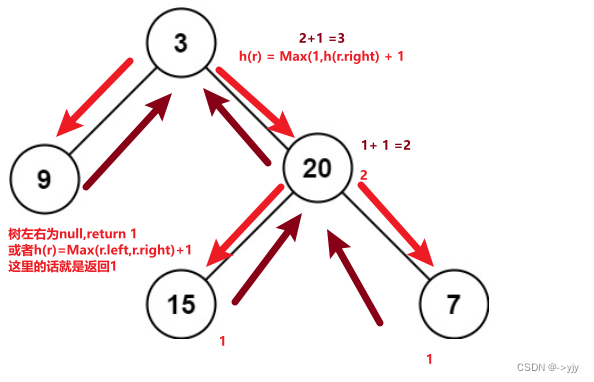
/**
* 二叉树最大深度-使用后序遍历求解
*/
public class Leetcode104_1 {
/*
思路:
1.得到左子树深度,得到右子树深度,二者最大值+1就是本节点深度
2.因为需要先得到左右子树深度,很显然是后序遍历典型应用
3.关于深度的定义:从根出发,离根最远的节点总边数
注意:力扣里的深度定义要多一
深度2 深度3 深度1
1 1 1
/ \ / \
2 3 2 3
\
4
*/
public int maxDepth(TreeNode node){
if(node==null){
return 0;
}
if(node.left==null&&node.right==null){
return 1;
}
int d1 = maxDepth(node.left);
int d2 = maxDepth(node.right);
return Integer.max(d1,d2)+1;
}
}
注:上面代码中其实可以把第二个if去掉
第二种解法:
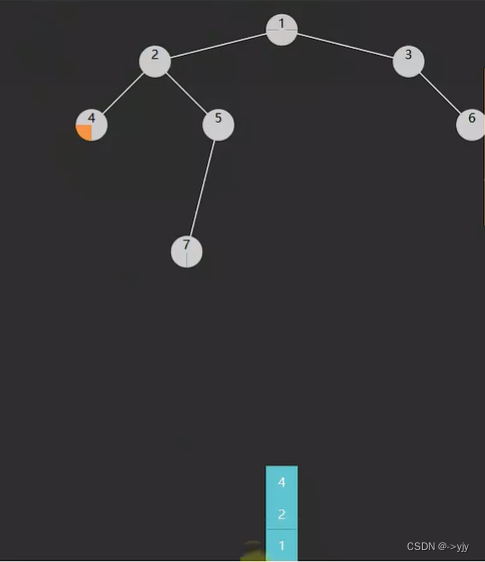

import java.util.LinkedList;
/**
* 二叉树最大深度 - 使用后序遍历(非递归)求解
*/
public class E05Leetcode104_2 {
/*
思路:
1.使用非递归后序遍历,栈的最大高度即为最大深度
*/
public int maxDepth(TreeNode root){
TreeNode curr = root;
TreeNode pop = null;
LinkedList<TreeNode>stack = new LinkedList<>();
int max = 0;//栈的最大高度
while(curr!=null || !stack.isEmpty()){
if(curr!=null){
stack.push(curr);
int size = stack.size();
if(size>max){
max = size;
}
curr=curr.left;
}else{
TreeNode peek = stack.peek();
if(peek.right==null||peek.right==pop){
pop=stack.pop();
}else{
curr=peek.right;
}
}
}
return max;
}
}
第三张方法:
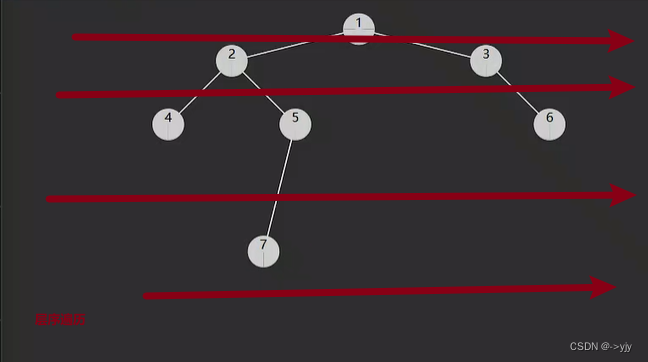
代码实现:
public class E05Leetcode104_3 {
/*
思路:
1.使用层序遍历,层数即最大深度
*/
public int maxDepth(TreeNode root){
Queue<TreeNode> queue= new LinkedList<>();
//LinkedList:可以作为双向链表,队列,栈 "身兼数职"
queue.offer(root);
int depth=0;
// int c1=1;//记录每层有几个元素
while(!queue.isEmpty()){
//queue.size()
// int c2=0;
int size = queue.size();
for(int i=0;i<size;i++){
TreeNode poll = queue.poll();
// System.out.print(poll.val+"\t");
if(poll.left!=null){
queue.offer(poll.left);
// c2++;
}
if(poll.right!=null){
queue.offer(poll.right);
// c2++;
}
}
// c1=c2;
// System.out.println();
depth++;
}
return depth;
}
}if(root==null){
return 0;
}
//有可能传过来的是nullclass Solution {
public int minDepth(TreeNode root) {
if(root==null)return 0;
int m1 = minDepth(root.left);
int m2 = minDepth(root.right);
return root.left==null||root.right==null?m1+m2+1:Math.min(m1,m2)+1;
}
}class Solution {
public int minDepth(TreeNode root){
if(root == null){
return 0;
}
Queue<TreeNode>queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while(!queue.isEmpty()){
int size = queue.size();
depth++;
for(int i=0;i<size;i++){
TreeNode poll = queue.poll();
if(poll.right==null&&poll.left==null){
return depth;
}
if(poll.left!=null){
queue.offer(poll.left);
}
if(poll.right!=null){
queue.offer(poll.right);
}
}
}
return depth;
}
}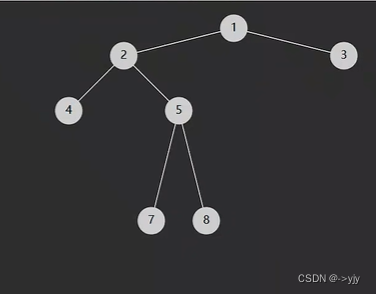
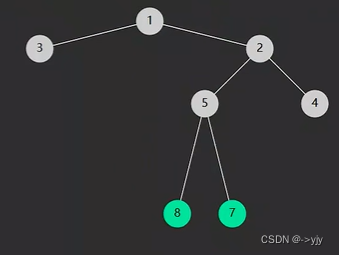
class Solution {
public TreeNode invertTree(TreeNode root) {
fn(root);
return root;
}
private void fn(TreeNode node){
if(node==null){
return;
}
TreeNode t = node.left;
node.left = node.right;
node.right = t;
fn(node.left);
fn(node.right);
}
}import java.util.LinkedList;
/**
* 根据后缀表达式构造表达式树
*/
public class ExpressionTree {
public static class TreeNode {
public String val;
public TreeNode left;
public TreeNode right;
public TreeNode(String val) {
this.val = val;
}
public TreeNode(TreeNode left, String val, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return this.val;
}
}
/*
中缀表达式 (2-1)*3
后缀(逆波兰)表达式 21-3*
1.遇到数字入栈
2.遇到运算符出栈,建立节点关系,再入栈
栈
/ /
/ /
/ /
----
'-'.right = 1
'-'.left = 2
'*' .right = 3
'*' .left = '-'
表达式树
*
/ \
- 3
/ \
2 1
*/
public TreeNode constructExpressionTree(String[] tokens) {
LinkedList<TreeNode> stack = new LinkedList<>();
for (String t : tokens) {
switch (t) {
case "+", "-", "*", "/" -> {//运算符
TreeNode right = stack.pop();
TreeNode left = stack.pop();
TreeNode parent = new TreeNode(t);
parent.left = left;
parent.right = right;
stack.push(parent);
}
default -> {//数字
stack.push(new TreeNode(t));
}
}
}
return stack.peek();
//做个后序遍历 检测
}
}
import Tree.ExpressionTree;
import org.junit.Test;
import java.util.ArrayList;
import static org.junit.Assert.assertArrayEquals;
public class TestExpressionTree {
ExpressionTree exp = new ExpressionTree();
@Test
public void test1(){
String[] tokens = {"2","1","-","3","*"};
ExpressionTree.TreeNode root = exp.constructExpressionTree(tokens);
ArrayList<String>result = new ArrayList<>();
post(root,result);
assertArrayEquals(tokens,result.toArray(new String[0]));
}
private void post(ExpressionTree.TreeNode node,ArrayList<String>result){
if(node==null){
return;
}
post(node.left,result);
post(node.right,result);
result.add(node.val);
}
}
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
import java.util.Arrays;
/**
* 根据前中序遍历结果构造二叉树
*/
public class Leetocde105 {
/*
preOrder = {1,2,4,3,6,7};
inOrder = {4,2,1,6,3,7};
根1
pre in
左 2 4 4,2
右 3,6,7 6,3,7
根 2
左 4
根 3
左 6
右 7
*/
public TreeNode buildTree(int[] preOrder,int[] inOrder){
if(preOrder.length==0||inOrder.length==0){
return null;
}
//创建根节点
int rootValue = preOrder[0];
TreeNode root = new TreeNode(rootValue);
//区分左右子树
for (int i = 0; i < inOrder.length; i++) {
if(inOrder[i]==rootValue){
//0 ~ i-1 左子树
//i+1 ~ inOrder.length-1 右子树
int[] inLeft = Arrays.copyOfRange(inOrder, 0, i);//i是不包含的 [4,2]
int[] inRight= Arrays.copyOfRange(inOrder, i, inOrder.length);//[6,3,7]
int[] preLeft = Arrays.copyOfRange(preOrder, 1, i + 1);//[2,4]
int[] preRight = Arrays.copyOfRange(preOrder, i+1, inOrder.length);//[3,6,7]
root.left = buildTree(preLeft,inLeft); //2
root.right = buildTree(preRight,inRight);//3
break;
}
}
return root;
}
}
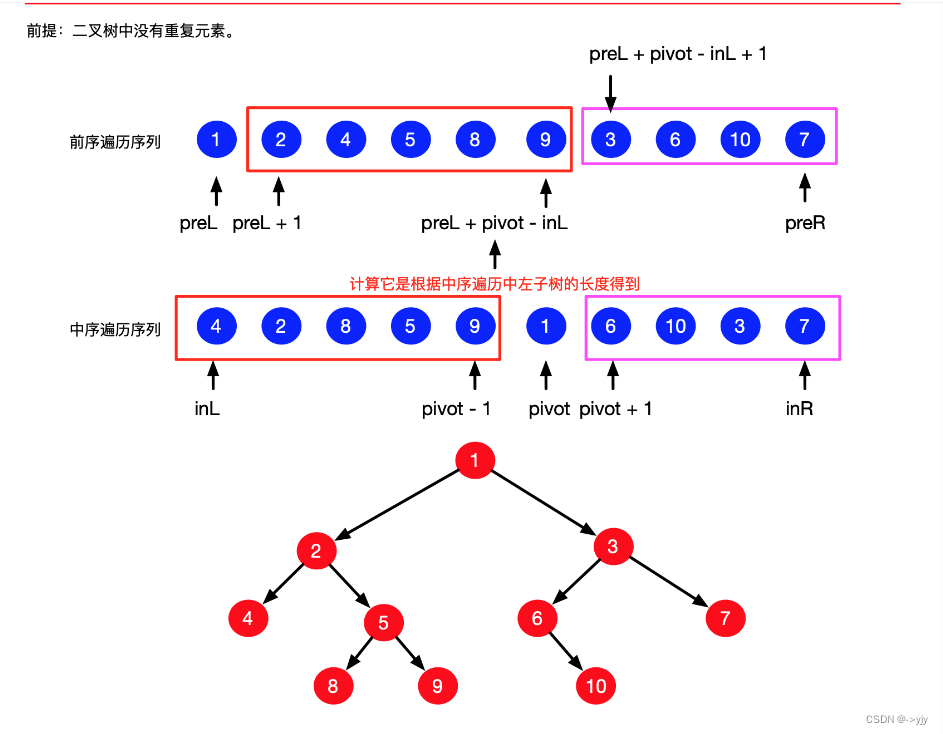
参考力扣题解:
可以将中序遍历的值和索引存在一个哈希表中,这样就可以一下子找到根结点在中序遍历数组中的索引。
Java
import java.util.HashMap;
import java.util.Map;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
private int[] preorder;
private Map<Integer, Integer> hash;
public TreeNode buildTree(int[] preorder, int[] inorder) {
int preLen = preorder.length;
int inLen = inorder.length;
if (preLen != inLen) {
throw new RuntimeException("Incorrect input data.");
}
this.preorder = preorder;
this.hash = new HashMap<>();
for (int i = 0; i < inLen; i++) {
hash.put(inorder[i], i);
}
return buildTree(0, preLen - 1, 0, inLen - 1);
}
private TreeNode buildTree(int preLeft, int preRight, int inLeft, int inRight) {
// 因为是递归调用的方法,按照国际惯例,先写递归终止条件
if (preLeft > preRight || inLeft > inRight) {
return null;
}
// 先序遍历的起点元素很重要
int pivot = preorder[preLeft];
TreeNode root = new TreeNode(pivot);
int pivotIndex = hash.get(pivot);
root.left = buildTree(preLeft + 1, pivotIndex - inLeft + preLeft,
inLeft, pivotIndex - 1);
root.right = buildTree(pivotIndex - inLeft + preLeft + 1, preRight,
pivotIndex + 1, inRight);
return root;
}
}
复杂度分析:
时间复杂度:O(N)O(N)O(N),这里 NNN 是二叉树的结点个数,每调用一次递归方法创建一个结点,一共创建 NNN 个结点,这里不计算递归方法占用的时间。
空间复杂度:O(N)O(N)O(N),这里忽略递归方法占用的空间,因为是对数级别的,比 NNN 小。
作者:liweiwei1419
链接:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solutions/8946/qian-xu-bian-li-python-dai-ma-java-dai-ma-by-liwei/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
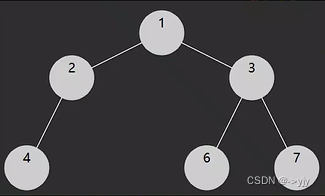
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder.length==0||postorder.length==0){
return null;
}
int rootValue = postorder[postorder.length-1];
TreeNode root = new TreeNode(rootValue);
for(int i=0;i<inorder.length;i++){
if(inorder[i] == rootValue){
int[] inLeft = Arrays.copyOfRange(inorder,0,i);
int[] inRight =Arrays.copyOfRange(inorder,i+1,inorder.length);
int[] postLeft = Arrays.copyOfRange(postorder,0,i);
int[] postRight = Arrays.copyOfRange(postorder,i,postorder.length-1);
root.left = buildTree(inLeft,postLeft);
root.right = buildTree(inRight,postRight);
}
}
return root;
}
}在我们之前所学的数据结构中我们要查找一个元素,时间复杂度都是O(n) 如果我们想提高查找效率就要引入新的数据结构和算法了
之前学过二分查找
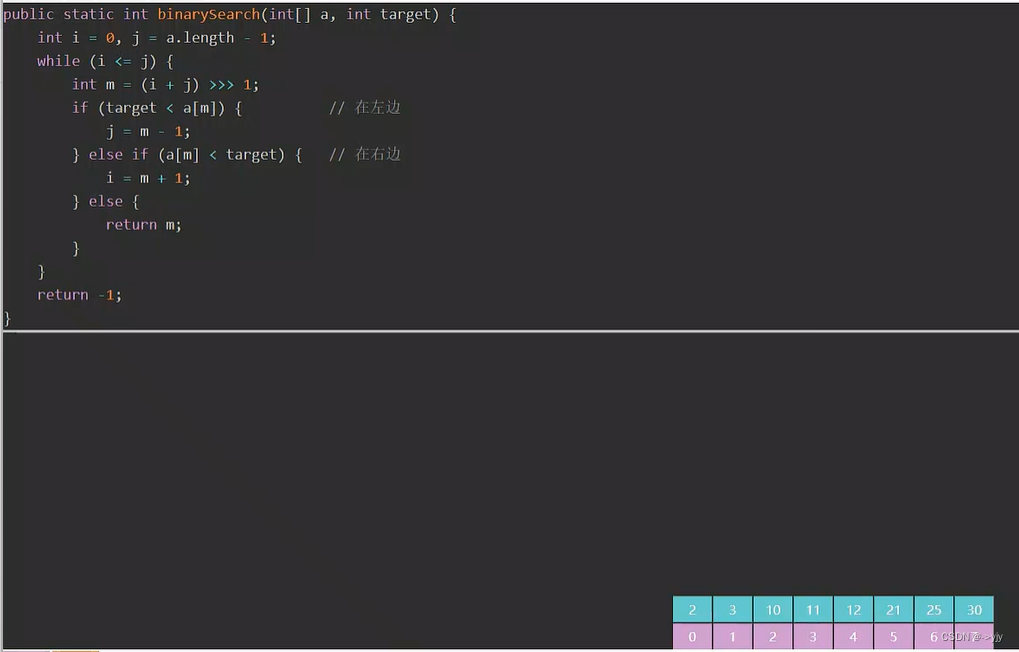
O(logN) 但是这个算法它必须是排好序的 但排序消耗的时间复杂度也是比较高的可能会得不偿失
那么我引入这个新的数据结构叫:
二叉搜索树
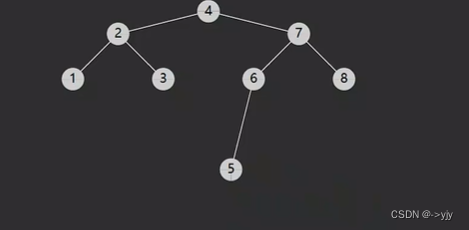

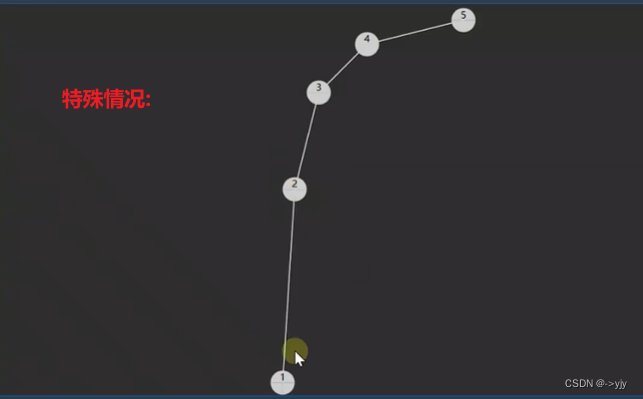
平均复杂度是对数时间,但是最糟糕情况是O(n)
get方法的实现
/**
* Binary Search Tree 二叉搜索树
*/
public class BSTTree1 {
BSTNode root;//根节点
static class BSTNode {
int key;
Object value;
BSTNode left;
BSTNode right;
public BSTNode(int key){
this.key = key;
}
public BSTNode(int key, Object value) {
this.key = key;
this.value = value;
}
public BSTNode(int key, Object value, BSTNode left, BSTNode right){
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
/**
* <h3>查找关键字对应的值</h3>
* @param:key-关键字
* @return:关键字对应的值
*/
public Object get(int key){
return doGet(root,key);
}
//递归版本
//尾递归 最后一步调用自身的时候(不含任何其他数) 转换成非递归实现性能更好 因为java不会对尾递归进行优化
private Object doGet(BSTNode node,int key){
if(node == null){
return null;//没有找到
}
if(key<node.key){
return doGet(node.left,key);//向左找
}else if(node.key < key){
return doGet(node.right,key);//向右找
}else{
return node.value;//找到了
}
}
//非递归版本
public Object get(int key){
BSTNode node =root;
while(node!=null){
if(key<node.key){
node = node.left;
}else if(key>node.key){
node = node.right;
}else{
return node.value;
}
}
return null;
}也可以用泛型实现更一般的方法:
/*
//泛型有没有比较大小的能力呢? 泛型中也有一个语法叫做泛型上限
将来我的泛型必须是Comparable的子类型
*/
public class BSTNode2<T extends Comparable<T>,V> {
static class BSTNode<T,V> {
T key;
V value;
BSTNode<T,V> left;
BSTNode<T,V> right;
public BSTNode(T key){
this.key = key;
}
public BSTNode(T key, V value) {
this.key = key;
this.value = value;
}
public BSTNode(T key, V value, BSTNode<T,V> left, BSTNode<T,V> right){
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
BSTNode<T,V> root;
/**
* <h3>查找关键字对应的值</h3>
* @param:key-关键字
* @return:关键字对应的值
*/
public V get(T key){
BSTNode<T,V> p =root;
while(p!=null){
//key p.key
/*
-1 : key<p.key
0 : key=p.key
1 : key>p.key
*/
int result = key.compareTo(p.key);
if(result<0){
p = p.left;
}else if (result>0){
p = p.right;
}else{
return p.value;
}
}
return null;
}min-max的实现
/**
* <h3>查找最小关键字对应值</h3>
* @Returns:关键字对应的值
*/
// public Object min(){
// return doMin(root);
// }
public Object min(){
if(root==null){
return null;
}
BSTNode P = root;
while(P.left!=null){
P = P.left;
}
return P.value;
}
public Object doMin(BSTNode node){
if(node==null){
return null;
}
if(node.left == null){//找到了最小的节点
return node.value;
}
return doMin(node.left);//尾递归
}
/**
* <h3>查找最大关键字对应值</h3>
* @return:关键字对应值
*/
public Object max(){
if(root==null){
return null;
}
BSTNode p = root;
while(p.right!=null){
p = p.right;
}
return p.value;
}
put的实现 --和java map集合非常相似
/**
* <h3>存储关键字和对应值</h3>
* @param:key 关键字
* @param:value 值
*/
public void put(int key,Object value){
//1.key 有 更新
//2.key 没有 更新
BSTNode node = root;
BSTNode parent =null;
while(node!=null){
parent = node;
if(key <node.key){
node = node.left;
}else if(node.key<key){
node=node.right;
}else{
//1
node.value = value;
return;
}
}
if(parent == null){//树为空
root = new BSTNode(key,value);
return;
}
//2
// new BSTNode(key,value);
if(key< parent.key){
parent.left = new BSTNode(key,value);
}else if(key> parent.key){//也可以直接改为else即可
parent.right = new BSTNode(key,value);
}
}
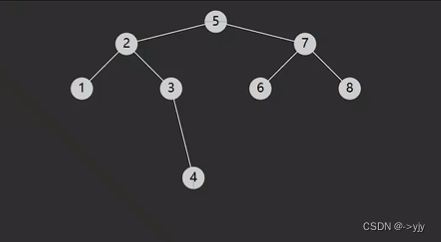
前驱&后继
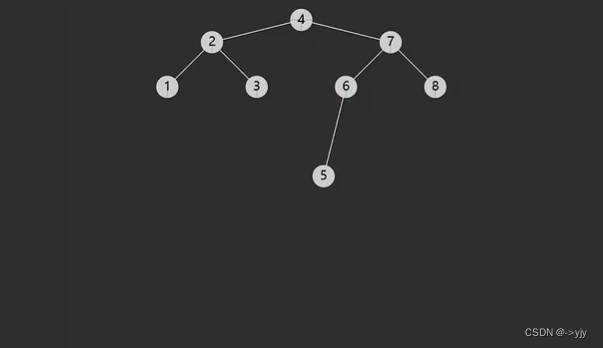

/**
* <h3>查找关键字的前驱值</h3>
* @param:key-关键字
* @return:前驱值
*/
//中序遍历结果就是升序的结果
//但是我们实际去实现的时候并不会采用中序遍历 因为性能不高 最坏的情况两个指针要把整个树走一次
/*
前人的经验:
分为有左子树时,此时前驱节点就是左子树的最大值,图中属于这种情况的有
没有左子树时,若离它最近的祖先从左而来,此时祖先为前驱
*/
public Object successor(int key) {
BSTNode p = root;
BSTNode ancestorFromLeft = null;
while(p!=null){
if(p.key < key){
ancestorFromLeft = p;
p = p.right;
}else if(p.key > key){
p = p.left;
}else{
break;
}
}
//没找到节点的情况
if(p==null){
return null;
}
//找到节点
if(p.left!=null){
return max(p.left);
}
//情况二:节点没有左子树(自左而来)
return ancestorFromLeft!=null?ancestorFromLeft.value:null;
}在这里也修改了一下max的代码
/**
* <h3>查找最大关键字对应值</h3>
* @return:关键字对应值
*/
public Object max(){
return max(root);
}
//写的更通用 方便找前驱等使用
private Object max(BSTNode node){
if(node==null){
return null;
}
BSTNode p = node;
while(p.right!=null){
p = p.right;
}
return p.value;
}后继

/**
* <h3>查找关键字的后继值</h3>
* @param:key-关键字
* @return:后继值
*/
public Object predecessor(int key){
BSTNode p = root;
BSTNode ancestorFromRight = null;
while(p!=null){
if(p.key < key){
p = p.right;
}else if(p.key > key){
ancestorFromRight = p;
p = p.left;
}else{
break;
}
}
//没找到节点的情况
if(p==null){
return null;
}
//找到节点
if(p.right!=null){
return min(p.right);
}
//情况二:节点没有右子树(自右而来)
return ancestorFromRight!=null?ancestorFromRight.value:null;
}public Object min(){
return min(root);
}
private Object min(BSTNode node){
if(node==null){
return null;
}
BSTNode P = node;
while(P.left!=null){
P = P.left;
}
return P.value;
}删除delete

第一种情况:没有左孩子

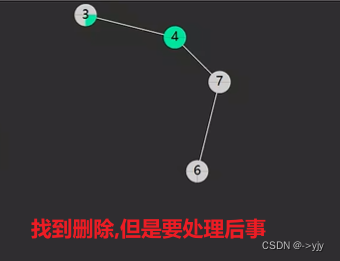
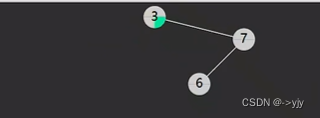
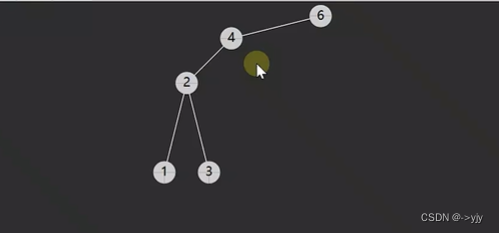
情况二:没有右孩子
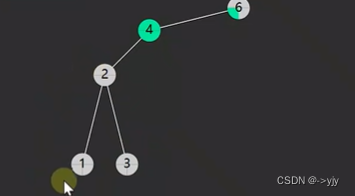
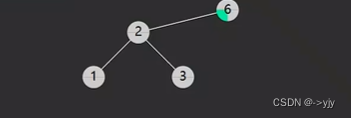
/**
* <h3>根据关键字删除</h3>
* @param:key-关键字
* @return:被删除关键字对应值
*/
public Object delete(int key){
//先找到节点
BSTNode parent =null;//记录待删除节点的父亲
BSTNode p = root;
while(p!=null){
if(key<p.key){
parent = p;
p = p.left;
}else if(p.key < key){
parent = p;
p = p.right;
}else{
break;
}
}
if(p==null){
return null;
}
//找到了进行删除操作
if(p.left==null && p.right!=null){
//情况一:
shift(parent,p,p.right);
}else if(p.right==null&&p.left!=null){
//情况二:
shift(parent,p,p.left);
}
return p.value;
}
/**
* 托孤方法
* @param parent-被删除节点的父亲
* @param deleted-被删除节点
* @param child-被顶上去的节点
*/
private void shift(BSTNode parent,BSTNode deleted,BSTNode child){
if(parent==null){
root = child;
}else if(deleted==parent.left){
parent.left = child;
}else{
parent.right =child;
}
}情况三:直接走情况一或者情况二的逻辑即可 直接将if 和 else if && 后面那部分删了即可

情况四: 后继相邻 & 后继不相邻(后继要先处理自己的后事)
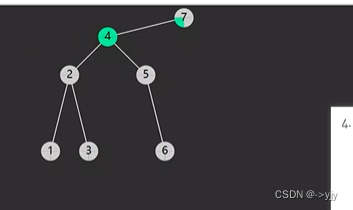
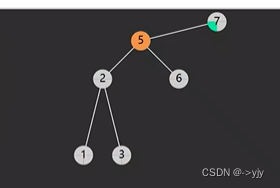

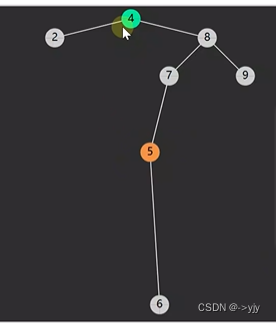
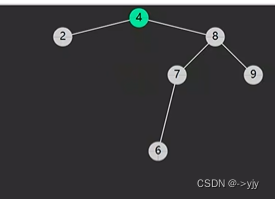
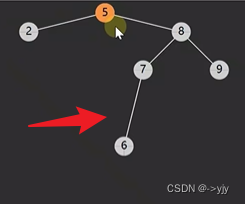
public Object delete(int key){
//先找到节点
BSTNode parent =null;//记录待删除节点的父亲
BSTNode p = root;
while(p!=null){
if(key<p.key){
parent = p;
p = p.left;
}else if(p.key < key){
parent = p;
p = p.right;
}else{
break;
}
}
if(p==null){
return null;
}
//找到了进行删除操作
if(p.left==null){
//情况一:
shift(parent,p,p.right);
}else if(p.right==null){
//情况二:
shift(parent,p,p.left);
}else{//情况四
//4.1被删除节点的后继节点
BSTNode s = p.right;
BSTNode sParent=p;//后继父亲
while(s.left!=null){
sParent = s;
s= s.left;
}
//后继节点即为s
if(sParent!=p){
//说明不相邻
4.2删除节点和后继节点不相邻,要处理后继的后事
shift(sParent,s,s.right);//不可能有左孩子 因为是后继
s.right = p.right;
}
//4.3后继取代被删除节点
shift(parent,p,s);
s.left = p.left;
}
return p.value;
}
整体代码:
/**
* Binary Search Tree 二叉搜索树
*/
public class BSTTree1 {
BSTNode root;//根节点
static class BSTNode {
int key;
Object value;
BSTNode left;
BSTNode right;
public BSTNode(int key){
this.key = key;
}
public BSTNode(int key, Object value) {
this.key = key;
this.value = value;
}
public BSTNode(int key, Object value, BSTNode left, BSTNode right){
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
/**
* <h3>查找关键字对应的值</h3>
* @param:key-关键字
* @return:关键字对应的值
*/
//非递归版本
public Object get(int key){
BSTNode node =root;
while(node!=null){
if(key<node.key){
node = node.left;
}else if(key>node.key){
node = node.right;
}else{
return node.value;
}
}
return null;
}
/**
* <h3>查找最小关键字对应值</h3>
* @Returns:关键字对应的值
*/
// public Object min(){
// return doMin(root);
// }
public Object min(){
return min(root);
}
private Object min(BSTNode node){
if(node==null){
return null;
}
BSTNode P = node;
while(P.left!=null){
P = P.left;
}
return P.value;
}
public Object doMin(BSTNode node){
if(node==null){
return null;
}
if(node.left == null){//找到了最小的节点
return node.value;
}
return doMin(node.left);//尾递归
}
/**
* <h3>查找最大关键字对应值</h3>
* @return:关键字对应值
*/
public Object max(){
return max(root);
}
//写的更通用 方便找前驱等使用
private Object max(BSTNode node){
if(node==null){
return null;
}
BSTNode p = node;
while(p.right!=null){
p = p.right;
}
return p.value;
}
/**
* <h3>存储关键字和对应值</h3>
* @param:key 关键字
* @param:value 值
*/
public void put(int key,Object value){
//1.key 有 更新
//2.key 没有 更新
BSTNode node = root;
BSTNode parent =null;
while(node!=null){
parent = node;
if(key <node.key){
node = node.left;
}else if(node.key<key){
node=node.right;
}else{
//1
node.value = value;
return;
}
}
if(parent == null){//树为空
root = new BSTNode(key,value);
return;
}
//2
// new BSTNode(key,value);
if(key< parent.key){
parent.left = new BSTNode(key,value);
}else if(key> parent.key){//也可以直接改为else即可
parent.right = new BSTNode(key,value);
}
}
/**
* <h3>查找关键字的前驱值</h3>
* @param:key-关键字
* @return:前驱值
*/
//中序遍历结果就是升序的结果
//但是我们实际去实现的时候并不会采用中序遍历 因为性能不高 最坏的情况两个指针要把整个树走一次
/*
前人的经验:
分为有左子树时,此时前驱节点就是左子树的最大值,图中属于这种情况的有
没有左子树时,若离它最近的祖先从左而来,此时祖先为前驱
*/
public Object successor(int key) {
BSTNode p = root;
BSTNode ancestorFromLeft = null;
while(p!=null){
if(p.key < key){
ancestorFromLeft = p;
p = p.right;
}else if(p.key > key){
p = p.left;
}else{
break;
}
}
//没找到节点的情况
if(p==null){
return null;
}
//找到节点
if(p.left!=null){
return max(p.left);
}
//情况二:节点没有左子树(自左而来)
return ancestorFromLeft!=null?ancestorFromLeft.value:null;
}
/**
* <h3>查找关键字的后继值</h3>
* @param:key-关键字
* @return:后继值
*/
public Object predecessor(int key){
BSTNode p = root;
BSTNode ancestorFromRight = null;
while(p!=null){
if(p.key < key){
p = p.right;
}else if(p.key > key){
ancestorFromRight = p;
p = p.left;
}else{
break;
}
}
//没找到节点的情况
if(p==null){
return null;
}
//找到节点
if(p.right!=null){
return min(p.right);
}
//情况二:节点没有右子树(自右而来)
return ancestorFromRight!=null?ancestorFromRight.value:null;
}
/**
* <h3>根据关键字删除</h3>
* @param:key-关键字
* @return:被删除关键字对应值
*/
public Object delete(int key){
//先找到节点
BSTNode parent =null;//记录待删除节点的父亲
BSTNode p = root;
while(p!=null){
if(key<p.key){
parent = p;
p = p.left;
}else if(p.key < key){
parent = p;
p = p.right;
}else{
break;
}
}
if(p==null){
return null;
}
//找到了进行删除操作
if(p.left==null){
//情况一:
shift(parent,p,p.right);
}else if(p.right==null){
//情况二:
shift(parent,p,p.left);
}else{//情况四
//4.1被删除节点的后继节点
BSTNode s = p.right;
BSTNode sParent=p;//后继父亲
while(s.left!=null){
sParent = s;
s= s.left;
}
//后继节点即为s
if(sParent!=p){
//说明不相邻
4.2删除节点和后继节点不相邻,要处理后继的后事
shift(sParent,s,s.right);//不可能有左孩子 因为是后继
s.right = p.right;
}
//4.3后继取代被删除节点
shift(parent,p,s);
s.left = p.left;
}
return p.value;
}
/**
* 托孤方法
* @param parent-被删除节点的父亲
* @param deleted-被删除节点
* @param child-被顶上去的节点
*/
private void shift(BSTNode parent,BSTNode deleted,BSTNode child){
if(parent==null){
root = child;
}else if(deleted==parent.left){
parent.left = child;
}else{
parent.right =child;
}
}
}
递归实现delete
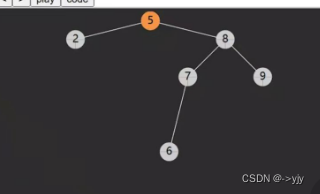
/**
* <h3>根据关键字删除</h3>
*
* @param:key-关键字
* @return:被删除关键字对应值
*/
public Object delete(int key) {
ArrayList<Object>result = new ArrayList<>();//保存被删除节点的值
root = doDelete(root,key,result);
return result.isEmpty()?null:result.get(0);
}
/*
递归版
1.删除节点没有左孩子,将右孩子托孤给Parent
2.删除节点没有右孩子,将左孩子托孤给Parent
3.删除节点左右孩子都没有,已经被涵盖在情况一,情况二当中,把null托孤给Parent
4.删除左右节点孩子都有,可以把它的后继节点(称之为S)托孤给parent
4
/ \
2 6
/ \
1 7
node : 起点
返回值: 删剩下的孩子节点 或 null
*/
private BSTNode doDelete(BSTNode node, int key,ArrayList<Object>result) {
if (node == null) {
return null;
}
if (key < node.key) {
node.left = doDelete(node.left, key,result);//假如要删除2 那么返回1
return node;
}
if (node.key < key) {
node.right = doDelete(node.right, key,result);
return node;
}
//找到了
result.add(node.value);
//情况1: 只有右孩子
if (node.left == null) {
return node.right;//返回的就是删剩下的东西
}
//情况2: 只有左孩子
if (node.right == null) {
return node.left;//返回的就是删剩下的东西
}
//情况3: 两个孩子都有
BSTNode s = node.right;///后继节点
while (s.left != null) {
s = s.left;
}
s.right = doDelete(node.right, s.key,new ArrayList<>());//反正这个new的用不上 因为是删除后继节点的
s.left = node.left;
return s;
}范围查询
/*
范围查询
*/
//中序遍历-->升序
/*
4
/ \
2 6
/ \ /\
1 3 5 7
*/
//找 < key 的所有value
public List<Object>less(int key){ //key = 6
ArrayList<Object>result = new ArrayList<>();
BSTNode p = root;
LinkedList<BSTNode> stack = new LinkedList<>();
while(p!=null||!stack.isEmpty()){
if(p!=null){
stack.push(p);
p=p.left;
}else{
BSTNode pop = stack.pop();
//处理值
if(pop.key<key){
result.add(pop.value);
}else{
break;
}
p = pop.right;
}
}
return result;
}
//找>key的所有value
/*
Pre-order,NLR
In-order,LNR
Post-order,LRN
Reverse Pre-order,NRL
Reverse In-order,RNL
Reverse post-order,RLN
*/
public List<Object>greater(int key){ //优化 从后开始 反向中序遍历
// ArrayList<Object>result = new ArrayList<>();
// BSTNode p = root;
// LinkedList<BSTNode> stack = new LinkedList<>();
// while(p!=null||!stack.isEmpty()){
// if(p!=null){
// stack.push(p);
// p=p.left;
// }else{
// BSTNode pop = stack.pop();
// //处理值
// if (key<pop.key){
// result.add(pop.value);
// }
// //不能提前结束 因为ta要把全部走一次
// p = pop.right;
//
//
// }
// }
// return result;
ArrayList<Object>result = new ArrayList<>();
BSTNode p = root;
LinkedList<BSTNode> stack = new LinkedList<>();
while(p!=null||!stack.isEmpty()){
if(p!=null){
stack.push(p);
p=p.right;
}else{
BSTNode pop = stack.pop();
//处理值
if (key<pop.key){
result.add(pop.value);
}
else{
break;
}
// System.out.println(pop.value);//逆序
p = pop.left;
}
}
return result;
}
//找>=key1||<=key2的所有值
public List<Object>between(int key1,int key2){
ArrayList<Object>result = new ArrayList<>();
BSTNode p = root;
LinkedList<BSTNode> stack = new LinkedList<>();
while(p!=null||!stack.isEmpty()){
if(p!=null){
stack.push(p);
p=p.left;
}else{
BSTNode pop = stack.pop();
//处理值
if(pop.key>=key1 && pop.key<=key2){
result.add(pop.value);
}else if(pop.key>key2){
break;
}
p = pop.right;
}
}
return result;
}
二叉搜索树练习
上面实现写过的就不做实现了.
删除节点-力扣450题
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
- 当然要注意的是:题目中的树节点TreeNode相当于例题中的BSTNode
- val,left,right(val即作为键又作为值)
- key,value,left,right
- Ta的TreeNode没有key,比较用的是TreeNode.val属性与待删除key进行比较
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode node, int key) {
if(node==null){
return null;
}
if(key<node.val){
node.left = deleteNode(node.left,key);
return node;
}
if(node.val<key){
node.right = deleteNode(node.right,key);
return node;
}
if(node.left==null){//情况一:只有右孩子
return node.right;
}
if(node.right == null){//情况二:只有左孩子
return node.left;
}
TreeNode s = node.right;//情况三:有两个孩子
while(s.left != null){
s= s.left;
}
s.right = deleteNode(node.right,s.val);
s.left = node.left;
return s;
}
}也可以这么写:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null){
return null;
}
if(key > root.val){
root.right = deleteNode(root.right,key);//去右子树删除
}
else if(key<root.val){
root.left = deleteNode(root.left,key);//去左子树删除
}
else{//当前节点就是要删除的节点
if(root.left==null){
return root.right;//情况一
}
if(root.right==null){
return root.left;//情况二
}
TreeNode node = root.right;//情况三
while(node.left!=null){//寻找要删除节点右子树的最左节点
node = node.left;
}
node.left = root.left;
//将要删除节点的左子树成为其右子树的最左节点的左子树
root = root.right;//将要删除节点的右子顶替它的位置,节点被删除
}
return root;
}
}新增节点-力扣701
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
/**
* 新增节点(题目前提:val一定与树中节点不同)
*/
public class Leetcode701 {
/*
put(key,value)
- key 存在 更新
- key 不存在 新增
*/
/*
val=7
5
/ \
2 6
/ \ \
1 3 7
*/
public TreeNode insertIntoBST(TreeNode node,int val){
if(node==null){//找到空位
return new TreeNode(val);
}
if(val<node.val){
//2.left = 2 多余的赋值动作
node.left = insertIntoBST(node.left,val);//val=1 建立父子关系
}else if(node.val<val){
node.right = insertIntoBST(node.right,val);
}
return node;
}
}
查询节点-力扣700
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root==null){
return null;
}
if(val<root.val){
return searchBST(root.left,val);
}else if(root.val<val){
return searchBST(root.right,val);
}else{
return root;
}
}
}验证二叉搜索树-力扣98
// 解法1:中序遍历非递归实现
public boolean isValidBST(TreeNode node){
TreeNode p = node;
LinkedList<TreeNode> stack = new LinkedList<>();
long prev=Long.MIN_VALUE;//代表上一个值
while(p!=null || !stack.isEmpty()){
if(p!=null){
stack.push(p);
p= p.left;
}else{
TreeNode pop = stack.pop();
//处理值
if(prev >= pop.val){
return false;
}
prev = pop.val;
p = pop.right;
}
}
return true;
}
long pre = Long.MIN_VALUE;
// 解法2:中序遍历递归实现
public boolean isValidBST(TreeNode node){
if(node==null){
return true;
}
boolean a = isValidBST(node.left);
//值
if(pre >= node.val){
return false;
}
pre = node.val;
boolean b = isValidBST(node.right);
return a&&b;
}虽然在leetcode上这段代码运行的效率比非递归的高 但是仍然不是最优效率的,下面来看一下:
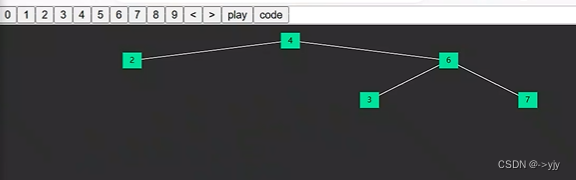
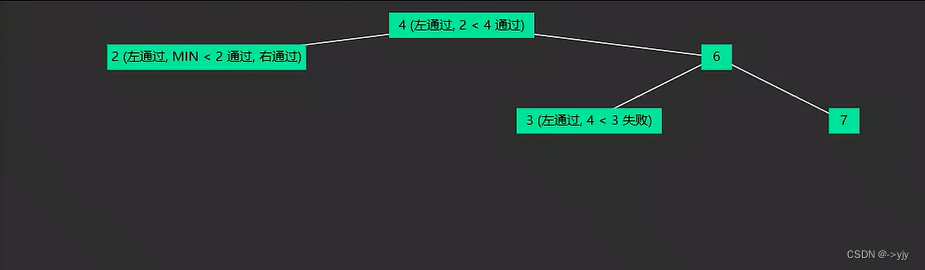
上面这段代码到这里仍然没有结束

long pre = Long.MIN_VALUE;
// 解法2:中序遍历递归实现
public boolean isValidBST(TreeNode node){
if(node==null){
return true;
}
boolean a = isValidBST(node.left);
if(!a){
return false;//做一个提前的返回
}
//值
if(pre >= node.val){
return false;
}
pre = node.val;
return isValidBST(node.right);;
}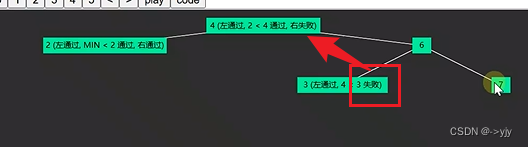
剪枝操作.
还有一个问题就是pre 变量的一个小坑:
public boolean isValidBST(TreeNode node){
return doValid(node,Long.MIN_VALUE);
}
private boolean doValid(TreeNode node,long prev){
if(node==null){
return true;
}
boolean a = doValid(node.left,prev);
if(!a){
return false;
}
if(prev>=node.val){
return false;
}
prev = node.val;
return doValid(node.right,prev);
/*
3
\
4
/
5
*/
}
这样写看似没有问题 但在运行像上面345这个实例的时候会发生问题 实际上当3往下走的时候4会先走doValid(node.left,prev); 这样看似prev = node.val 也就是 prev = 5,但因为你的prev是作为一个参数,是对整个方法中生效的,也就是4这个点有doValid(node.left,prev) 和 doValid(node.right,prev)这两个prev都是4这个点传入的prev并不会说因为在doValid(node.prev)中prev=5导致这个方法的所有prev都变为了5,本质也就是这个参数只是这个方法的局部变量,局部变量的修改不会影响到其他的方法
解决方法:1.prev作为全局变量(上面实现过) 2.AtomicLong prev也就是作为是一个对象
public boolean isValidBST(TreeNode node){
return doValid(node,new AtomicLong(Long.MIN_VALUE));
//始终传递的都是同一个对象 所以修改可以改变其他方法中prev
//那能不能用Long 这个长整型作为对象呢?不行,Long和其他java
//里的包装类型都属于不可变数据类型,里面的值是不能修改的
//AtomicLong是可变数据类型,里面的数据是可以用set修改
}
private boolean doValid(TreeNode node, AtomicLong prev){
if(node==null){
return true;
}
boolean a = doValid(node.left,prev);
if(!a){
return false;
}
if(prev.get()>=node.val){
return false;
}
prev.set(node.val);
return doValid(node.right,prev);
}
上面的所有方法都是利用中序遍历判断,
能否只判断父亲比左孩子大比右孩子小?no 考虑少了
/*
能否只判断父亲比左孩子大,比右孩子小?
4
/ \
2 6
/ \
1 3
反例:
4
/ \
2 6
/ \
3 7
只考虑了父子之间没有考虑祖先跟后代的大小关系,判断上就出现了疏漏
*/可以用上下限的方法来解决:
/*
-∞ 4 +∞
/ \
-∞ 2 4 4 6 +∞
/ \
4 3 6 6 7 +∞
*/
//解法4:上下限递归实现 0ms
public boolean isValidBST4(TreeNode node){
return doValid4(node,Long.MIN_VALUE,Long.MAX_VALUE);
}
private boolean doValid4(TreeNode node,long min,long max){
if(node==null){
return true;
}
if(node.val<=min || node.val>=max){
return false;
}
return doValid4(node.left,min,node.val) && doValid4(node.right,node.val,max);
}搜索二叉树范围和-力扣938
// 解法1: 中序非递归实现 4ms
public int rangeSumBST(TreeNode node,int low,int high){
TreeNode p = node;
LinkedList<TreeNode>stack = new LinkedList<>();
int sum = 0;
while(p!=null||!stack.isEmpty()){
if(p!=null){
stack.push(p);
p=p.left;
}else{
TreeNode pop = stack.pop();
//处理值
if(pop.val>high){
break;
}//剪枝
if(pop.val >= low){
sum+=pop.val;
}
p = pop.right;
}
}
return sum;
}解题思路
标签:深度优先遍历
题意:这个题字面含义很难理解,本意就是求出所有 X >= L 且 X <= R 的值的和
递归终止条件:
当前节点为 null 时返回 0
当前节点 X < L 时则返回右子树之和
当前节点 X > R 时则返回左子树之和
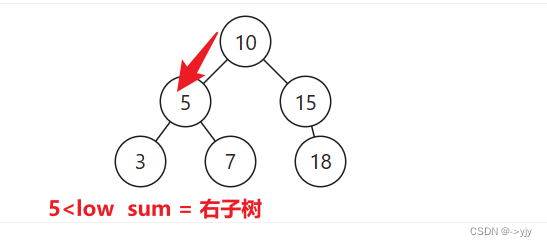
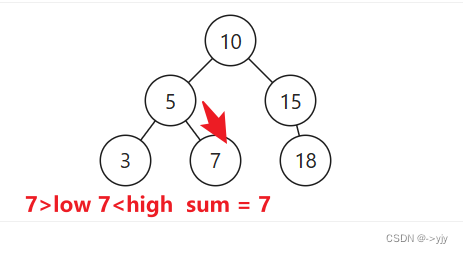
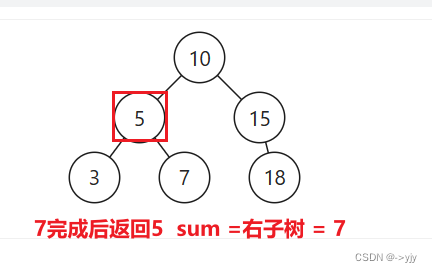
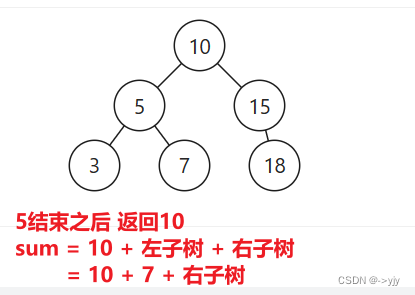
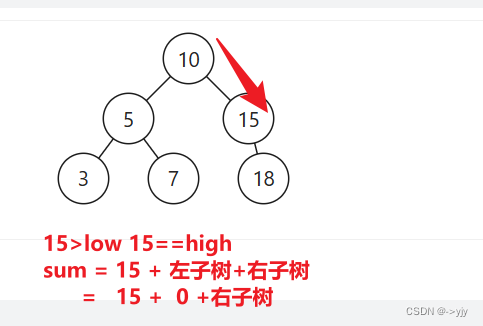
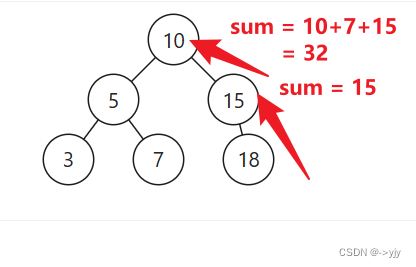
当前节点 X >= L 且 X <= R 时则返回:当前节点值 + 左子树之和 + 右子树之和
//中序遍历性能不高的原因在于不能够有效的筛选 对high可以剪枝 但是对low没有办法有效的剪枝
// 解法2:上下限递归
/*
10
/ \
5 15
/ \ \
3 7 18 low=7 high=15
*/
public int rangeSumBST(TreeNode node,int low,int high){
if(node==null){
return 0;
}
if(node.val<low){
return rangeSumBST(node.right,low,high);
}
if(node.val>high){
return rangeSumBST(node.left,low,high);
}
// 在范围内
return node.val + rangeSumBST(node.left, low, high) + rangeSumBST(node.right, low, high);
}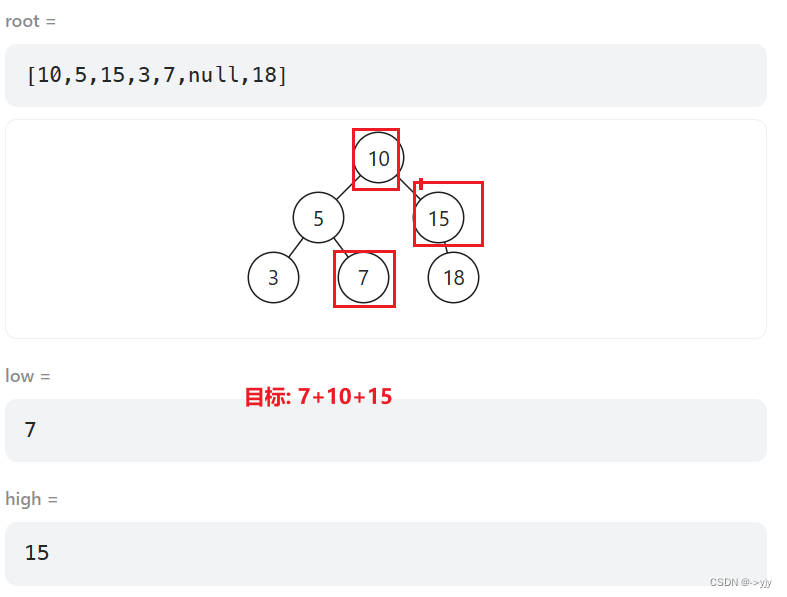


前序遍历构造二叉搜索树-力扣1008
/**
* 根据前序遍历构造二叉搜索树 题目说明 preorder 长度>=1
*/
public class Leetcode1008 {
/*
1.preorder长度>=1
2.preorder没有重复值
8, 5, 1, 7, 10, 12
8
/ \
5 10
/ \ \
1 7 12
*/
public TreeNode bstFromPreorder(int[] preorder){
TreeNode root = new TreeNode(preorder[0]);
for (int i = 1; i < preorder.length; i++) {
int val = preorder[i];
insert(root,val);//n * log(n)
}
return root;
}
private TreeNode insert(TreeNode node,int val){
if(node==null){
return new TreeNode(val);
}
if(val<node.val){
node.left = insert(node.left,val);
}else if(node.val<val){
node.right = insert(node.right,val);
}//没有重复值 直接不写else
return node;
}
}方法二:

// 上限法 8 5 1 7 10 12
/*
1.遍历数组中的每一个值,根据值创建节点
- 每个人节点若成功创建:做孩子上限,右孩子上限
2.处理下一个值时,如果超过此上限,那么
- 将null作为上个节点的孩子
- 不能创建节点对象
- 直到不超过上限为止
3.重复1,2步骤
*/
public TreeNode bstFromPreorder(int[] preorder){
return insert(preorder,Integer.MAX_VALUE);
}
/*
依次处理 preorder 中每个值,返回创建好的节点或null
1.如果超过上限,返回null,作为孩子返回
2.如果没超过上限,创建节点,并设置其左右孩子
左右孩子完整后返回
*/
int i = 0;//索引从0开始
private TreeNode insert(int[] preorder,int max){
if(i==preorder.length){
return null;
}
int val = preorder[i];
if(val>max){
return null;
}
//没有超过上限
TreeNode node = new TreeNode(val);
i++;//找到下一个值看看下一个值能不能作为左孩子或者右孩子
node.left = insert(preorder,val);//左孩子上限就是自身的值
node.right= insert(preorder,max);//
return node;
}上下限:时间复杂度为O(n)
分治法:O(n*logn)
//分治法
/*
8 5 1 7 10 12
根 8
左 5 1 7
右 10 12
根 5 左 1 右 7
根 10 左 null 右 12
*/
public TreeNode bstFromPreorder1(int[] preorder){
return partition(preorder,0,preorder.length);
}
private TreeNode partition(int[] preorder,int start,int end){
if(start>end){
return null;
}
TreeNode root = new TreeNode(preorder[start]);
int index = start+1;
while(index<=end){
if(preorder[index]>preorder[start]){
break;
}
index++;
}
//index是右子树的起点
root.left = partition(preorder,start+1,index-1);
root.right = partition(preorder,index,end);
return root;
}
求二叉搜索树最近公共祖先(祖先也包括自己) - 力扣235
/**
* 求二叉搜索树最近公共祖先(祖先也包括自己)
* 前提:
* <ul>
* <li>节点值唯一</li>
* <li>p和q都存在</li>
* </ul>
*/
public class Leetcode235 {
/*
_ _ 6_ _
/ \
2 8
/ \ / \
0 4 7 9
/ \
3 5
待查找节点p q 在某一节点的两侧,那么此节点就是最近的公共祖先
*/
public TreeNode lowestCommonAncestor(TreeNode root,TreeNode p,TreeNode q){
TreeNode a = root;
while(p.val<a.val&&q.val<a.val || a.val<p.val && a.val<q.val){ //在同一侧
if(p.val<a.val){
a = a.left;
}else{
a= a.right;
}
}
return a;
}
}原文地址:https://blog.csdn.net/2301_79602614/article/details/137374742
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!