【模型仿真】基于粒子群模糊控制PSO-fuzzy的EV电动汽车模型仿真

摘要
本文研究了一种基于粒子群优化(PSO)模糊控制的电动汽车(EV)能量管理系统模型,通过结合PSO算法和模糊控制,实现对电动汽车电池电流和车辆速度的优化控制。仿真结果表明,该方法能够有效改善电动汽车的动力性能与能量消耗。
理论
1. 粒子群优化算法(PSO)
粒子群优化算法是一种基于群体智能的优化方法,通过模拟群体中个体之间的信息共享,逐步逼近最优解。PSO算法由粒子的位置和速度构成,迭代更新公式如下:
-
速度更新公式:
v i (t+1)=w⋅v i (t)+c 1 ⋅rand()⋅(p best −x i (t))+c 2 ⋅rand()⋅(g best −x i (t))
-
位置更新公式:
x i (t+1)=x i (t)+v i (t+1)
2. 模糊控制 模糊控制是一种基于语言规则的控制方法,通过模糊化、规则推理和去模糊化三个步骤,对非线性系统进行控制。
模糊控制规则如:
-
IF 速度误差大 THEN 控制输出强
-
IF 电流变化小 THEN 控制输出弱
3. PSO-fuzzy 结合
PSO用于优化模糊控制器的隶属函数参数和控制规则,从而提高控制器的性能。
实验结果
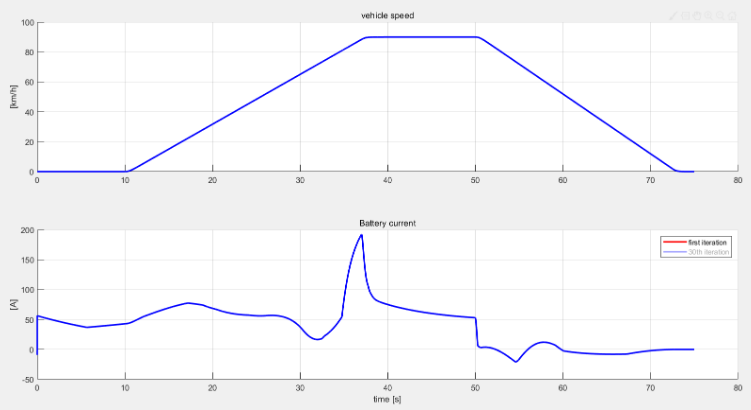
实验使用Matlab对车辆速度和电池电流进行了仿真,仿真结果显示了车辆在不同加速与减速阶段的速度变化和电池电流响应。
-
车辆速度:车辆速度在0至100 km/h之间变化,符合设定的速度目标。
-
电池电流:电池电流在加速阶段增大,减速阶段有效回收能量,表现出良好的能量管理效果。
部分代码
% PSO-fuzzy 电动汽车能量管理控制
% 初始化粒子群参数
num_particles = 30; % 粒子数
num_iterations = 50; % 迭代次数
dim = 5; % 参数维度
w = 0.8; % 惯性权重
c1 = 2; % 个体学习因子
c2 = 2; % 社会学习因子
% 初始化粒子的位置和速度
x = rand(num_particles, dim);
v = rand(num_particles, dim);
% 模糊控制器
fuzzy_controller = readfis('fuzzy_controller.fis');
for iter = 1:num_iterations
for i = 1:num_particles
% 模糊控制仿真
output = evalfis(fuzzy_controller, x(i, :));
fitness(i) = -output; % 目标函数为负能耗
end
% 更新全局最优和个体最优
[best_fit, best_idx] = min(fitness);
g_best = x(best_idx, :);
% 更新速度和位置
for i = 1:num_particles
v(i, :) = w*v(i, :) + c1*rand()*(p_best(i, :) - x(i, :)) + c2*rand()*(g_best - x(i, :));
x(i, :) = x(i, :) + v(i, :);
end
end
参考文献
❝
Kennedy, J., & Eberhart, R. (1995). Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks.
Zadeh, L. A. (1965). Fuzzy Sets. Information and Control.
Zhang, H., & Wang, Y. (2018). Energy Management for Electric Vehicles Using PSO Optimized Fuzzy Logic Controller. Journal of Power Sources.
Wang, J., & Sun, C. (2020). Fuzzy Control in Electric Vehicle Applications. IEEE Transactions on Vehicular Technology.
(文章内容仅供参考,具体效果以图片为准)
原文地址:https://blog.csdn.net/2401_84610415/article/details/143698560
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
