清华大学提出基于ESKF的松耦合里程计RINO：一种具有非迭代估计的精确、稳健的雷达惯性里程计

Abstract

精确的定位和建图对于实现自动驾驶车辆的自主导航至关重要。然而，当GNSS信号失效或在极端天气条件（例如雾、雨和雪）下，车体运动估计仍然面临重大挑战。近年来，扫描雷达因其较强的穿透能力成为一种有效的解决方案。然而，扫描雷达数据本质上噪声较高，需通过成百上千次的优化迭代，才能从这些噪声数据中估计出可靠的转换结果。这种迭代求解既耗时、不稳定，又容易失败。为了解决这些挑战，我们提出了RINO，一种准确且稳健的雷达惯性里程计系统，它采用非迭代的求解方法。该方法分离旋转和平移估计，并通过自适应投票机制进行2D旋转估计，提高了效率，同时保证了解的时间一致性。此外，该方法在扫描雷达和惯性测量单元（IMU）之间实现了松耦合系统，利用了误差状态卡尔曼滤波（ESKF）。值得注意的是，我们成功估计了来自扫描雷达的位姿估计的不确定性，并将其纳入滤波器的最大后验估计中，这是以前被忽视的考量。通过在公开数据集上的验证，RINO在精度和鲁棒性上均优于现有的最先进方法和基线。

代码获取：https://github.com/yangsc4063/rino

 欢迎加入自动驾驶实战群

Introduction

自动驾驶车辆依赖于精确的定位，以确保安全和高效的导航。全球导航卫星系统（GNSS）被广泛应用且非常有效，但在树木和高楼等障碍物密集的城市环境中，其性能会显著下降。因此，越来越多的研究者探索利用车载传感器进行车体运动估计，尤其是在GNSS信号中断时，传感器可以补充甚至完全替代基于GNSS的系统。

在过去的二十年中，基于相机和LiDAR的多种里程计和SLAM方法相继被开发，并在性能上取得了显著成果。然而，这些方法在恶劣天气条件下（如雾、雨或雪）往往表现受限。相比之下，毫米波雷达由于其更长的操作波长，在这种条件下能够保持稳健性，因此成为一种具有前景的替代方案。然而，扫描雷达数据本质上噪声较大且容易产生显著失真，为设计有效的里程计或SLAM方法带来了挑战。

考虑到这些挑战，越来越多的研究者开始探索基于雷达的里程计解决方案。基于扫描雷达的现有雷达里程计方法主要分为稀疏和密集两类。密集方法直接处理扫描雷达获取的张量格式数据，而稀疏方法则从数据中提取关键点，再进行配准。在计算复杂度和精度方面，稀疏方法通常具有优势。大多数稀疏方法基于迭代最近点（ICP）算法，该算法是一种迭代方法，通过交替最近点匹配和配准残差来对齐两组点云。然而，尽管迭代方法可以有效减少异常值的影响并近似最佳估计，但也存在固有缺点：计算成本高、不稳定且易受局部最小值影响，从而导致失败。

3. METHODOLOGY

A. 系统概述

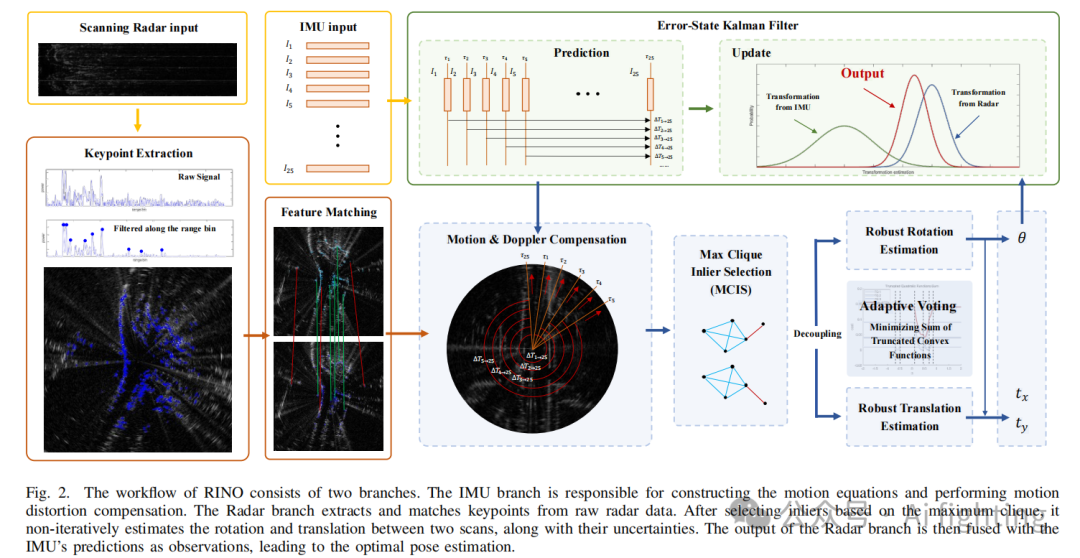
如图2所示，本文提出的流程名为 RINO，能够同时接收扫描雷达（4Hz）和IMU数据（100Hz）。我们希望利用这两种传感器的观测值来估计车辆状态。通用的状态估计可以被表述为最大后验概率 (MAP) 问题。假设运动过程满足马尔可夫性，可以使用滤波方法解决这个问题，该方法具有轻量级的优势。在滤波器中，IMU 测量值用于构建预测方程作为运动状态的先验估计，而扫描雷达分支的配准结果则作为位姿的观测值。下文将分别介绍 RINO 的这两个分支。

B. 状态估计

对于IMU，其状态变量包括：

其中，p 和 R∈SO(3)分别是 IMU 的位置和姿态，v是速度，

是IMU偏差，g 为重力。这些变量均相对于世界坐标系。然而，当用这些状态变量构建运动方程时，对旋转变量进行线性化成为一项难题。受 Fast-lio启发，我们将原始状态变量视为名义状态变量，其中名义值与真实值的差异代表误差状态变量。此外，噪声处理已被并入误差状态变量中。名义状态变量的运动学方程为：

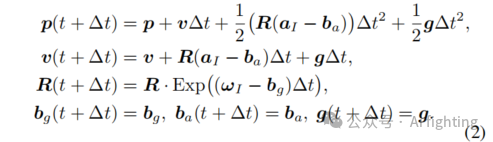
离散时间下的误差状态变量为：

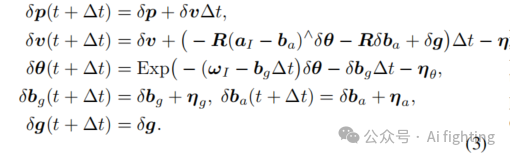
其中，Δt表示离散时间步长， 和 是IMU的测量值，而 和 是IMU测量的白噪声。是 在速度上的作用，满足 

，而 也有类似的关系。基于公式（2）和（3），我们执行ESKF的预测过程。由于噪声已被包含在误差状态中，可以直接根据公式（2）获得名义状态变量的预测。对于误差状态，有：

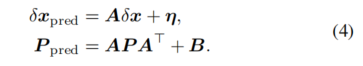
其中，P 是误差状态变量 的协方差估计矩阵，A 是将（3）式表达为矩阵乘法形式时得到的系数矩阵，B是  的噪声矩阵，其中个别变量噪声的协方差矩阵被对角排列。

在 ESKF 的预测步骤之后，位姿以 100Hz 的高频计算，与IMU的输出频率保持一致。这些高频但粗略的位姿估计可以部分缓解单帧数据中扫描雷达的动态失真问题。具体方法将在III-C节详细阐述。

在ESKF的更新过程中，来自RO的位置信息和姿态输出可以视为 RIO 系统中状态变量的观测值。设

 和 

 表示来自 RO 的某一时刻的观测值。我们可以直接将它们作为误差状态变量的观测值：

因此，观测方程变得相当简单：

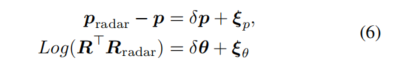
其中， 和 是来自 RO 的观测噪声（换言之，扫描雷达位姿估计的不确定性）。类似地，写出公式（6）的整体形式为：

观测矩阵 C可以简单地表示为：

噪声矩阵为

。基于这些步骤，可以如下执行 ESKF 的更新过程：

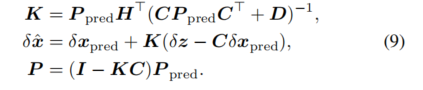
其中 c(⋅)表示观测函数。

在预测和更新步骤之后，有必要将误差状态纳入名义状态，即重置ESKF（设置 

）。需要注意的是，重置误差状态变量会导致旋转变量切线空间的零点发生变化。因此，协方差矩阵应相应调整：

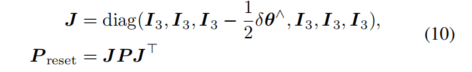
其中  表示重置前的误差状态变量估计，表示将向量表达为反对称矩阵。

C. 扫描雷达里程计

系统的RO（雷达里程计）流程与 ORORA 类似，后者作为基准方法。首先，从扫描雷达的原始强度-距离-角度数据中提取关键点。然后，使用 ORB 为每个点生成描述符，并通过暴力匹配建立上一帧扫描的关键点 

和当前帧扫描的关键点 

之间的对应关系集

。接下来，对这些对应关系应用动态失真和多普勒频移补偿。最后，补偿后的点对应关系用于点云配准，扫描间的变换会被累积。我们将旋转和位移的估计解耦，并采用加速的自适应投票方法，使得无需迭代即可快速计算旋转和位移。

雷达提取的关键点质量直接决定了生成点云地图的清晰度。评估了 cen2018和 cen2019后发现，cen2018 获得的关键点位置明显更准确。因此，我们选择了 cen2018，并限制了其最大距离，因为过远的点存在较高的不确定性，可能会对点云配准产生负面影响。此外，对原始数据进行了高通滤波，以增强信号峰值的显著性，从而优化关键点提取过程。

如前所述，我们利用 IMU 的高频位姿估计来补偿动态失真和多普勒频移。设扫描雷达的单次扫描时间为。在0到  时间段内，我们接收到来自IMU的25个位姿估计 T1, T2, …, Tend，每个都有时间戳 τ1, τ2, …, τend。通过插值 T1, T2, …, Tend，我们可以在0到 ts 时间内查询任意时间的雷达位姿。因此，可以将任意关键点的坐标转换为 τend 时的坐标以实现运动补偿。

其中，pτ 是 τ 时刻关键点的坐标，Tτ 是 τ 时刻插值后的 IMU 位姿，

 表示 IMU 与雷达之间的外参。

D. 非迭代求解的点云配准

在 Sec.III-C 中提到，使用对应关系集

来进行点云配准，以实现扫描间的里程计。我们在此详细说明该部分。我们将扫描雷达的鲁棒配准问题描述如下：

其中，R◦ 和 t◦ 分别表示旋转和位移的真实值。表示第 i 个点的对应关系是否正确；若正确，则 

，否则  可以取任意值。 表示测量噪声。由于扫描雷达原始数据中存在大量噪声和“鬼影”效应，对应关系集 

包含大量错误匹配。因此，我们采用截断最小二乘 (TLS) 估计来建立鲁棒点云配准的优化模型，尽可能降低对离群值的敏感性。

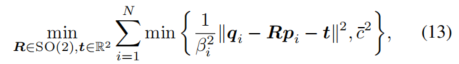
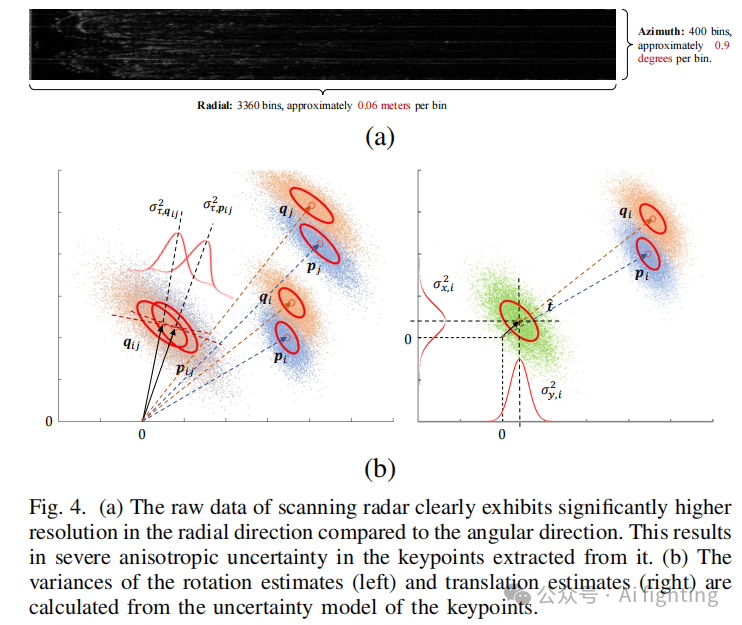
值得注意的是，公式（13）中的 表示噪声 的主要方差（即将二维高斯分布投影到各个方向后的方差上限）。这意味着在描述具有显著各向异性不确定性的雷达关键点时，该模型可能显得较为粗糙。

为了更好地捕捉关键点的不确定性并减少问题复杂性，我们将旋转和平移解耦。具体而言，我们在同一帧点云中对点对求差，以消除平移变换，从而获得与平移无关的测量值 (TIMs)：

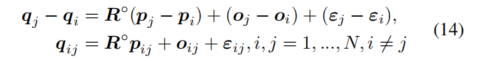
然后，我们计算平移-旋转无关测量值（TRIMs）的幅度：

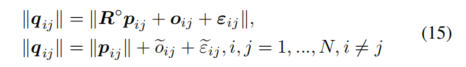
其中

。

首先，我们使用 TRIMs 

进行初步内点选择，仅需检查 ∥qk∥−∥pk∥ 是否小于预定义的阈值。

接下来，我们可以使用 TIMs 

来估计旋转变换，然后使用估计出的 ˆR 分别估计平移变换的两个分量。

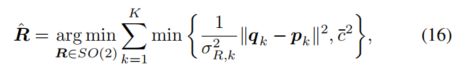
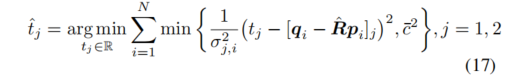
ORORA 使用 GNC 方法进行旋转估计，这是一种有效解决非凸优化问题的技术。然而，GNC 的迭代特性会导致不稳定的计算时间，并可能收敛到局部最小值，这可能会在轨迹估计中引入不连续性。为了克服这些限制，我们将旋转和位移估计的优化问题统一，采用自适应投票方法实现非迭代解法。此外，我们获得了旋转和位移估计的方差，作为 ESKF 更新过程的输入。

可以观察到二维旋转可以表示为标量（旋转角度）。因此，公式（14）和（16）可以重写为：

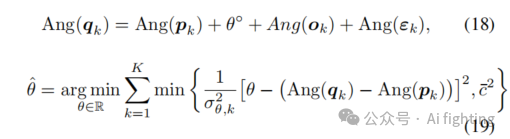
其中，Ang(·) 表示计算向量角度的函数。

这表明公式（19）和（17）的目标函数实际上具有相同的形式：标量变量的截断二次函数之和。对于此类优化问题，需要考虑两个关键问题。首先，如何估计决策变量的方差。其次，如何解决问题本身。

考虑第一个问题，旋转和位移的方差源于关键点的不确定性。

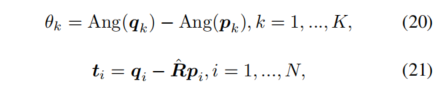
因此，讨论应从建模关键点的不确定性开始。我们高度认可 ORORA 对关键点各向异性不确定性的建模，因此采用了它。假设关键点 

 的不确定性在距离和方位上独立，满足独立的正态分布 

，其中 和 可从扫描雷达的极坐标数据中估计（如图 4(a) 所示）。关键点 被建模为正态分布 

，其中

 的值可以在文献中找到。

对于旋转，TIM 分布的协方差可由 

计算，然后投影到切向方向，如图 4(b) 左侧所示：

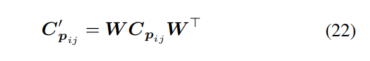
其中，W是将协方差从原坐标转换为以 为轴的坐标系的矩阵。然后，我们取

的 (1,1) 元素，记为 

，并除以  的幅度，以近似旋转角度分布的方差。然后，根据公式（20），可以得到旋转的方差：

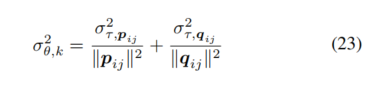
对于位移，我们需要利用之前获得的旋转 。根据公式（21），可以表示位移的协方差为 

。接下来，如图 4(b) 右侧所示，我们将位移分布投影到 x 和 y 方向。换句话说，我们取  的 (1,1) 和 (2,2) 元素，分别对应位移的两个分量的方差。

最后，我们解决了目标函数为截断二次函数之和的优化问题，这是使用非迭代方法解决点云配准的关键。将公式（19）和（17）表示为统一形式：

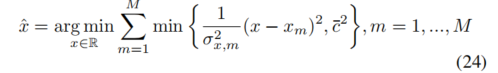
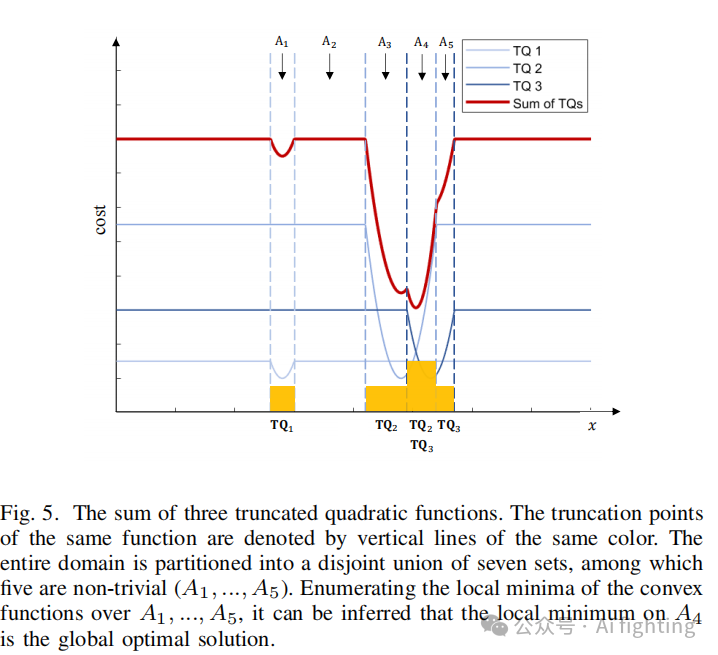
从图 5 中可以观察到，尽管目标函数在全局上是高度非凸的，但实际上是分段凸的。通过根据截断点

对定义域进行划分，可以使目标函数在每个分段上保持凸（甚至是二次的）。枚举所有分段，在每个分段上最小化目标函数，并选择所有局部最小值中的最小值即可确定全局最小值。令 

表示为 

，上述分段表示为

。我们的目标是计算与每个 对应的索引集

。

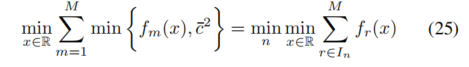
通过枚举以获得最优分段 ，我们寻求的最优估计值为：

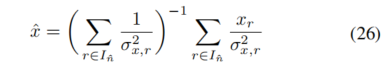
E. 位姿不确定性估计
我们发现，RINO 在运行过程中可能遇到一些极端情况。例如，提取的特征点可能过于稀疏，或者两帧之间存在过多动态物体，导致在 MCIS 之后剩余的内点数量较少，如图所示。这些问题可能会导致当前扫描雷达分支位姿估计的置信度下降。在这种情况下，我们希望 RINO 更倾向于信任来自 IMU 的位姿估计。自然地，我们可以从公式（26）估计

的方差。

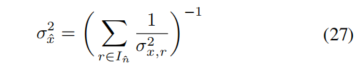
综上所述，所述的自适应投票用于分别估计旋转角度和两个位移分量及其不确定性。随后，这三个估计值及其不确定性可作为观测输入到卡尔曼滤波器的更新过程中（见 Sec.III-B），从而完成扫描雷达和 IMU 之间的自适应、松耦合状态估计。

IV. Experiment

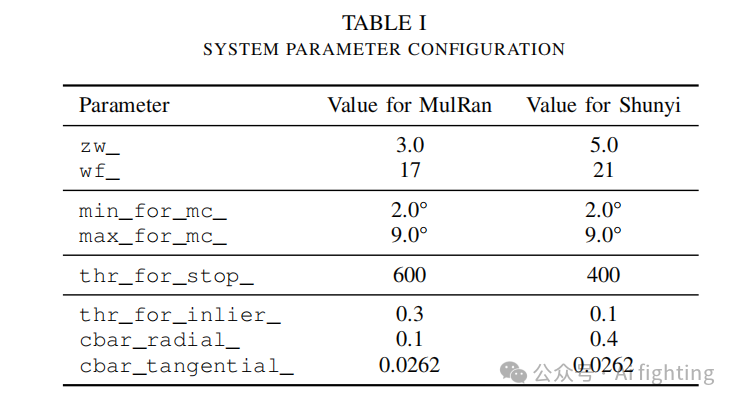
我们在表 I 中列出了所有参数，包括在 MulRan 数据集上的测试参数和用于真实世界测试的参数。这两组参数的差异主要是由于使用了不同的扫描雷达模型。需要注意的是，适用于 MulRan 的参数是在 DCC01 序列上调整获得的，并在其余序列测试期间保持不变，因为我们认为这种方式能使实验结果更具意义。

1. 定量评估

A. 基准测试

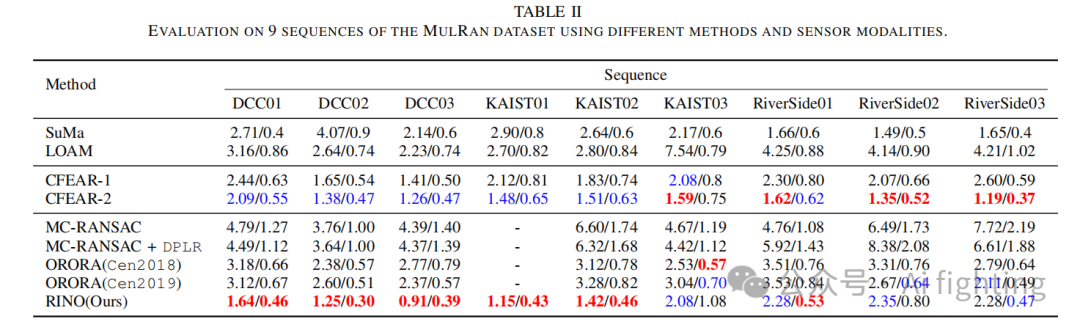
如表 II 所示。在大多数序列中，提出的方法减少了相对平移和旋转误差，尤其在 DCC 和 KAIST 数据集上表现出色。在某些序列中，结果优于次优算法 21.19%。相比基准 ORORA，RINO 显著提升了性能。在使用 Cen2018 和 Cen2019 特征点提取的 ORORA 基准上，RINO 分别在 DCC 和 KAIST 序列上实现了 91.51% 和 97.40% 的平均提升。在 DCC03 序列中，改进达到了 260.4%。此外，RINO 还全面超越了经典的 LiDAR 里程计方法 LOAM，在准确性上与先进方法 SuMa 相当。

在 Riverside 序列中，RINO 的里程计精度相较于 DCC 和 KAIST 序列显著下降。然而，某些性能指标仍保持在最佳或次优水平。一方面，Riverside 序列中的数据在河岸附近采集，这被认为是一个退化场景；另一方面，RINO 的性能下降比其他算法更为显著。可能的原因在于我们流程中固有的马尔科夫性假设。无论是 ESKF 还是基于全局点云配准的里程计，都是以增量方式运行的，当前的位姿变换估计仅与前一时刻相关。该方法在一定程度上忽视了局部地图中较大区域的点云结构信息，可能导致在退化环境中出现混淆。

综上所述，我们认为 RINO 在结构化环境中针对恶劣天气条件设计的当前里程计算法中实现了最优的精度性能。就所有场景的测试结果而言，RINO 被认为达到了与当前最先进算法相当的性能水平。

B. 消融研究
表 III结果表明，RO(GNC) 的性能较 ORORA 论文中的测试结果有所下降（表 II）。我们推测这种下降可能是由于参数设置的差异以及原始扫描雷达数据中精确方位编码信息的丢失。

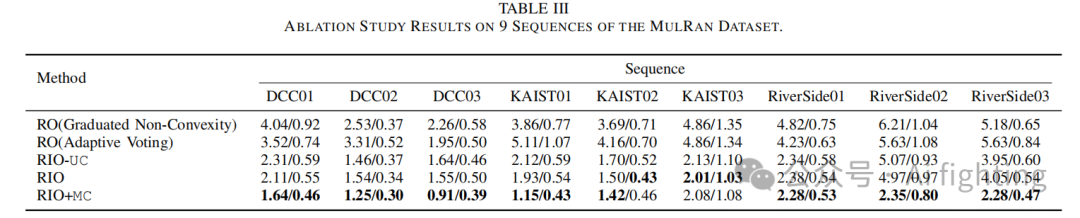
在比较 RO(GNC) 和 RO(AV) 时，两种方法在多个序列上的里程计误差相似。然而，RO(AV) 通常表现出比 RO(GNC) 更短的运行时间。此外，我们认为 RO(AV) 的稳健性比 RO(GNC) 更高。这表明，使用自适应投票方法进行旋转估计增强了系统的整体性能。

与这两种扫描毫米波雷达里程计方法相比，集成的定位和映射系统 (RIO) 在所有序列上的表现显著提高（74.26%），尤其是在 DCC01、DCC02、KAIST01、KAIST02、KAIST03 和 Riverside01 序列上。这表明将 IMU 与扫描雷达里程计进行松耦合显著提高了系统的准确性。

C. 算法运行时间
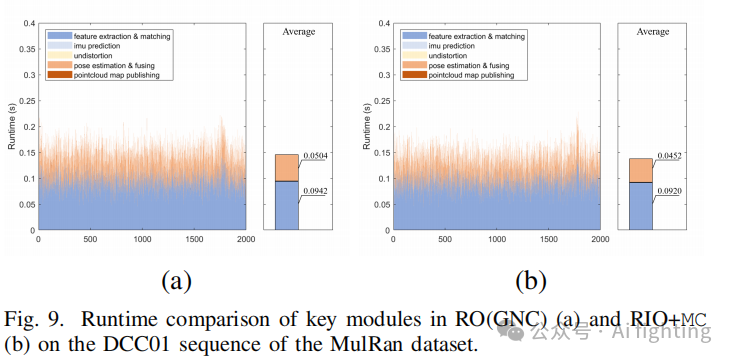
系统的平均运行时间约为 0.1381 秒，快于扫描毫米波雷达的采集频率 (4Hz)。通过对比图 9(a) 和图 9(b)，可以看出自适应投票的采用使点云配准模块的效率提升了近 11.5%。这一改进为原始鲁棒点云配准问题提供了更高效的解决方案，证明了所提出方法的有效性。

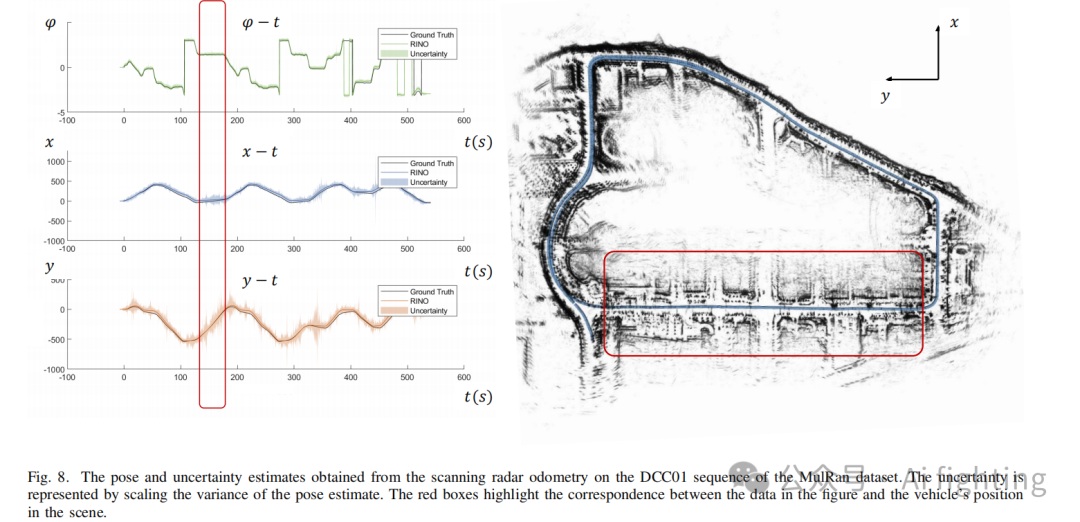
D. 位姿估计不确定性
图 8 中的红框标记了不确定性较高的区域，这些区域对应车辆沿直道从右向左行驶的情况。道路两侧建筑物的特征沿道路分布，形成沿 y 轴的退化构型，导致 y 方向上的不确定性增加。该观察表明位姿估计的不确定性与场景中特征的分布密切相关。

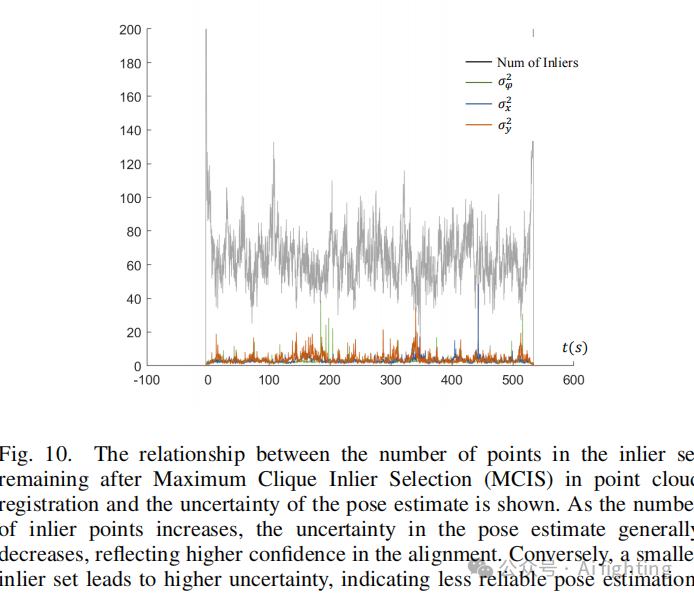
接下来，我们认为点云配准中最大团内点选择 (MCIS) 后剩余的内点数量也会影响位姿估计的不确定性。直观上，观测源越少，估计的置信度越低。这在图 10 中得到了验证，内点数量的低谷往往与位姿不确定性的峰值一致，表明内点数量与位姿估计的置信度之间存在直接关系。

VI. 定性评估

A. 对恶劣天气条件的鲁棒性
我们在 Boreas 数据集上的 2021-11-28-09-18 序列中展示了 RINO 的性能，如图 11 所示。图中展示了相机捕捉的同步图像数据。从相机的视角来看，可以明显看到当前天气条件十分恶劣，光线昏暗，地面覆盖着积雪，且有雪花飘落，部分遮挡了相机视野。微弱的光线和均匀的白雪模糊了相机图像中的纹理特征，而飘浮的雪花则对 LiDAR 扫描引入了显著噪声。这些极端的天气条件对视觉和基于 LiDAR 的里程计算法有不利影响。然而，实验结果显示，RINO 在这种不利的天气条件下基本不受影响，展现了其强大的鲁棒性。

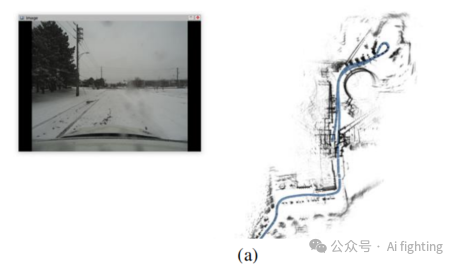
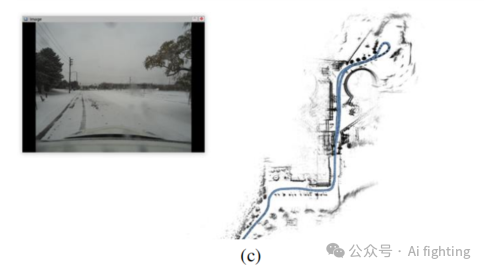
B. 在多样场景下的鲁棒性
我们通过在从未见过的环境中部署 RINO 于实际车辆上，验证了其可行性和鲁棒性。我们的数据采集车辆是一款 4×4 越野平台，配备了多种传感器，以支持不同的感知任务，如图 12 所示。车辆安装了一个高精度的 OxTS RT3000 定位系统（集成了 IMU），以及一个 NavTech CIRDEV-X 扫描雷达，位于车顶中央。其他传感器的配置在此处略去。

如图 13 所示，在两个环路的重访区域中，点云地图相对清晰。这表明，即使在复杂且剧烈的运动条件下，我们的算法依然保持了高精度的里程计估计，且点云地图能够准确反映卫星地图中的结构特征。

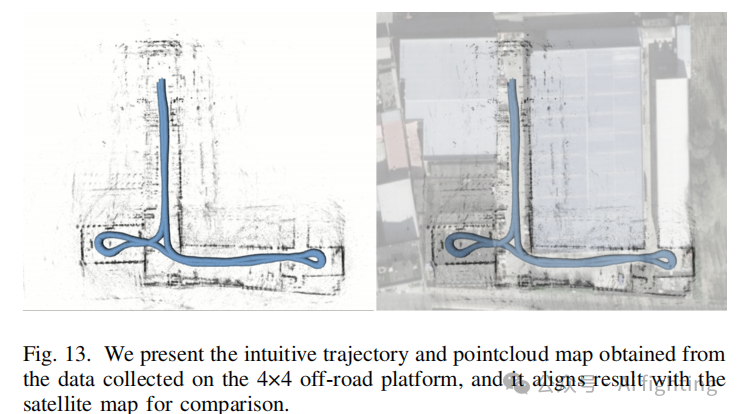
结论

主要贡献：

1. 提出了一种适用于高噪声和严重失真的扫描雷达数据的非迭代旋转和平移估计方法。该方法不仅减少了计算时间，还增强了估计过程的鲁棒性。
2. 提出了一种基于误差状态卡尔曼滤波（ESKF）的松耦合系统，在RINO中，扫描雷达实时计算的位姿估计不确定性可与IMU自适应融合，从而增强系统的环境适应性。
3. 在多个数据集上的广泛实验表明，RINO在各种场景和恶劣天气条件下具有较强的性能和适应性，并通过真实车辆测试验证了其实用性。

文章引用：RINO: Accurate, Robust Radar-Inertial Odometry with Non-Iterative Estimation

最后别忘了，帮忙点“在看”。  

您的点赞，在看，是我创作的动力。

AiFighing是全网第一且唯一以代码、项目的形式讲解自动驾驶感知方向的关键技术。

长按扫描下面二维码，加入知识星球。

原文地址：https://blog.csdn.net/laukal/article/details/143809197

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！