数据结构:归并排序
归并排序
时间复杂度O(N*logN)
如果两个序列有序,通过归并,可以让两个序列合并后也有序,变成一个有序的新数组
对于一个数组,如果他的左右区间都有序,就可以进行归并了
归并的方法
将数组的左右两个有序区间比较,每次都取出一个最小的,然后放入临时数组(不能在原数组上修改,因为修改原数组需要挪动数据,时间复杂度高)
但是对于任意一个数组而言,他的左右区间并不有序,如果想要使用归并排序,就要想办法取出数组的有序区间
这里可以使用递归拆分数组,当数组足够小(每一个区间都只有一个数据时),该区间就一定有序,就可以使用归并排序了

可以设置一个temp数组,用来存储分解的区间并进行排序,归并排序完成后再将temp拷贝回原数组的对应区间,直到递归完全结束(原数组有序)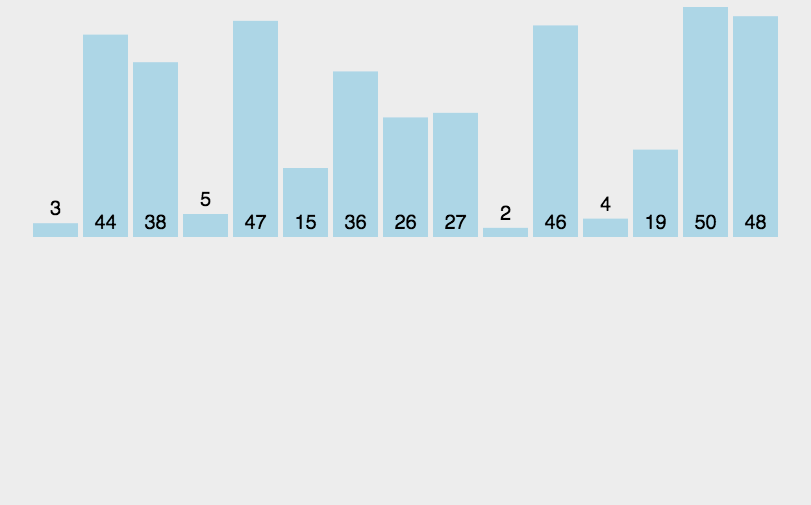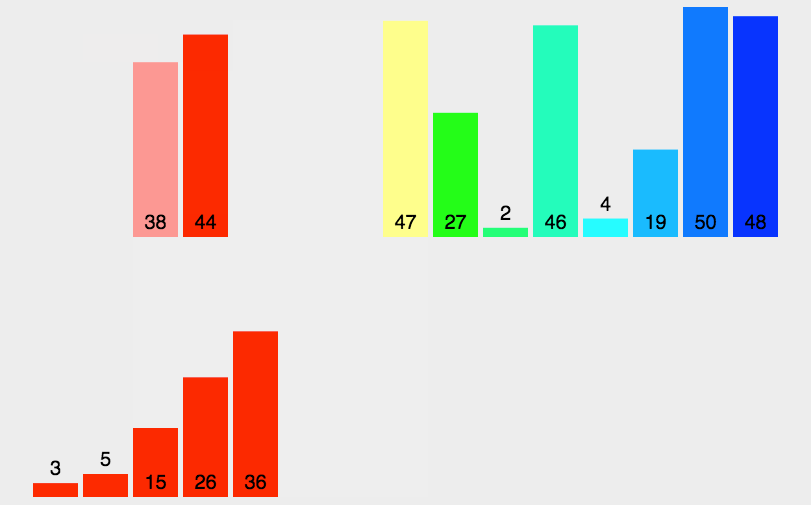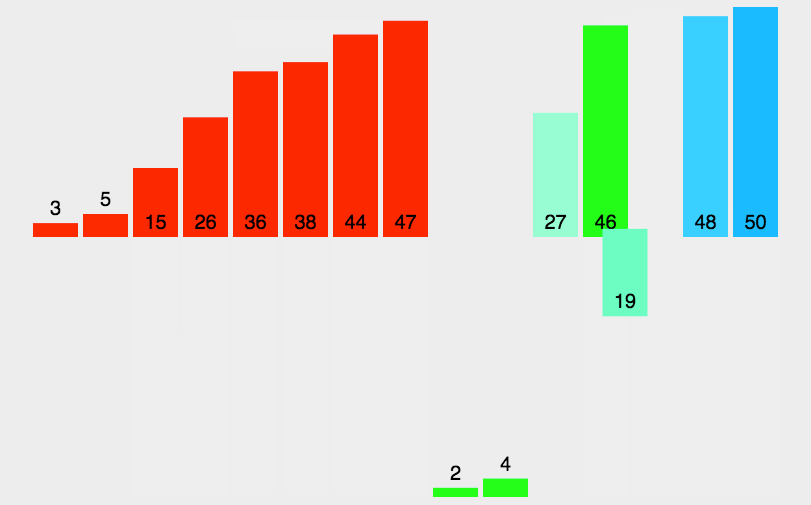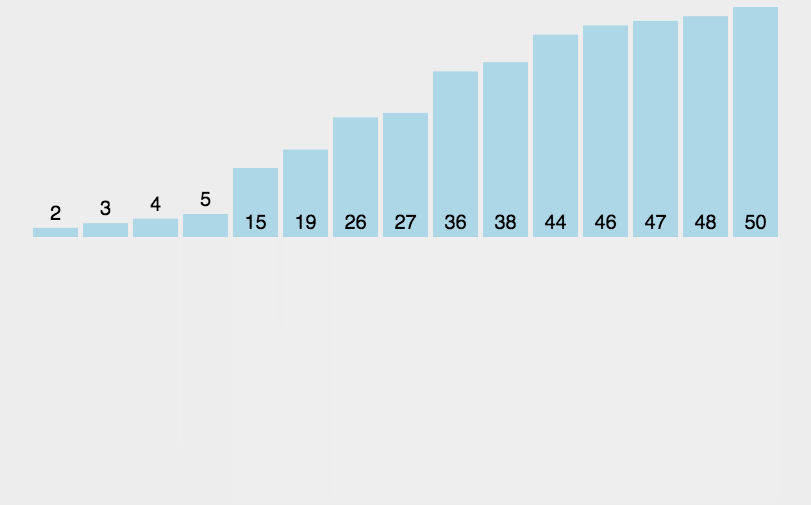
代码
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin == end)
return;
int mid = (begin + end) / 2;
//开始递归
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并
int begin1 = begin;
int end1 = mid;
int begin2 = mid + 1;
int end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//判断哪个区间全部放入tmp,再将另一个区间全部放入tmp
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//将归并好的区间拷贝会原数组
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail!");
return;
}
_MergeSort(a, 0, n - 1, tmp);
//释放tmp
free(tmp);
tmp = NULL;
}归并排序的非递归方法
归并排序需要将递归改为循环
不方便使用栈来实现,因为不同于快速排序类似前序遍历,归并排序的递归类似于二叉树的后序遍历
问题核心
归并排序需要两个区间进行归并,
而如果使用栈,则当取到需要归并的两个区间的第二个时
第一个区间就已经被pop出栈了,无法知道哪个区间需要和当前区间归并
解决方法
可以将数组看作一个一个数(一个数就是一个区间),然后每两个就进行归并
将归并后的两个数再看作一个区间,再与其他区间进行归并
即直接从叶子节点向前走(回溯)
可以设置gap = 2^n来归并每组数据
设置每个区间的首尾为b n(begin n),e n(end n)
eg.
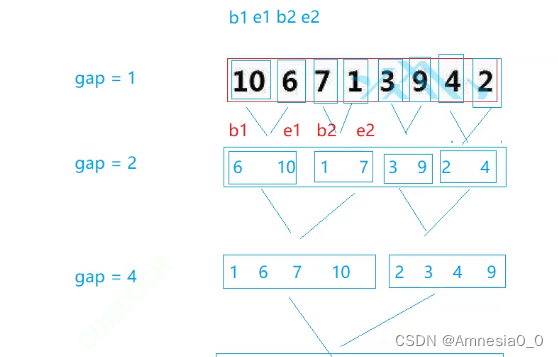
由图可知,e1 = b1 + gap - 1,b2 = b1 + gap
后续同理
基础代码框架(存在问题)
根据当前的思路,可以写出大概的代码
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)//一直归并到原数组大小
{
for (int j = 0; j < n; j += 2 * gap)//保证每一个区间都被取到
{
int begin1 = j, end1 = j + gap - 1;
int begin2 = j + gap, end2 = begin2 + gap - 1;
int i = j;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//判断哪个区间全部放入tmp,再将另一个区间全部放入tmp
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + j, tmp + j, sizeof(int) * 2 * gap);
}
gap *= 2;
}
free(tmp);
tmp == NULL;
}代码问题(数组越界)
当前代码可能存在数组的越界访问
理论上来讲,除了begin1 = j < n外,其他的begin2, end1, end2都可能越界
因此需要分开处理这些问题
1.end1越界
end1越界(end1后面就没有数据了)说明当前没有第二组数据,而第一组只有一部分,且有序
因此当前这一组就不需要再进行归并了,直接让这一组准备下一层归并
2.begin2越界
begin2越界也不用归并,原因与end1越界相同
3.end2越界
end2越界需要归并,因为在begin2与end2中还存在部分有序数据,因此需要归并组成新区间
但是想要归并就需要修正end2,保证end2不再越界
4.修改后的代码
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)//一直归并到原数组大小
{
for (int j = 0; j < n; j += 2 * gap)//保证每一个区间都被取到
{
int begin1 = j, end1 = j + gap - 1;
int begin2 = j + gap, end2 = begin2 + gap - 1;
int i = j;
if (end1 >= n || begin2 >= n)//end1和begin2越界,跳出当前循环,不归并
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//判断哪个区间全部放入tmp,再将另一个区间全部放入tmp
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1));//使用修正后的区间长度
}
gap *= 2;
}
free(tmp);
tmp == NULL;
}原文地址:https://blog.csdn.net/2301_80006788/article/details/137091812
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
