2024年大湾区杯粤港澳金融数学建模B题论文首发+60种模型组合讲解+代码手把手保姆级讲解+数据分享
大湾杯B题论文已经完成更新。本次论文问题一提供四种解题方法、问题二提供五种解题方法、问题三提供三种解题方法。累计4*5*3=60种方案随机组合,方便大家降重。每种方法提供matlab、python两套实现代码。
11.2日 18:00 发布降重说明
11.3日 18:00 发布选题人数统计
11.4日 18:00 漏洞问题答疑+售后群在线会议答疑
11.5日 18:00 发布无水印版本
11.6日 18:00 发布无水印代码、数据 【可直接提交版本】
数据中存在无法去除水印,直接提交使用存在问题。因倒卖获取该数据集而导致结果问题、论文问题,本数模社概不负责
42页正文 无附录 60种模型组合方案

数据集+问题一分享资料(问题一代码+论文+思路)链接:
链接:https://pan.baidu.com/s/139IMk3X5XDOQFMhP041Spg
提取码:sxjm
基于多模型集成的粤港澳大湾区经济增长预测与对比研究
摘要
粤港澳大湾区是中国经济发展的核心区域,其未来经济发展趋势对区域和国家的发展战略具有重要意义。本文旨在研究大湾区未来 5-10 年内经济增长的驱动因素,建立相应的数学模型来预测其经济走势,并提出有针对性的政策建议。
首先,数据处理方面,我们收集了包括人口、科技、物流、国际环境等指标在内的多维度数据,并对数据进行了缺失值插值、降维和相关性分析。为了减少数据的复杂度,对国际环境数据进行了主成分分析(PCA),对人口数据则采用 t-SNE 方法进行降维,以便从高维数据中提取主要特征。
在问题一的求解过程中,我们分析了粤港澳大湾区的历史、人口、科技、产业和经济状况等数据,建立了多元回归模型,量化评价了各因素对大湾区 GDP 的影响。通过相关性分析和降维操作,最终找到了影响 GDP 增长最为显著的几个关键因素。结果表明,科技投入和物流网络的完善对大湾区经济的正向影响最大,而人口年龄结构的变化也起到了一定的调节作用。
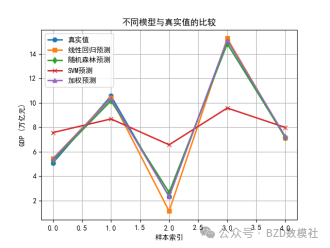
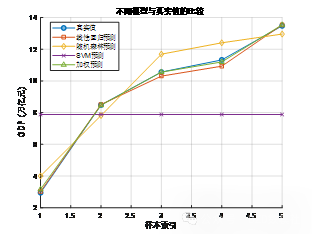
问题二主要针对未来 5-10 年的经济预测,采用了多种预测模型,包括线性回归、随机森林、BP 神经网络等。各模型的结果经过粒子群优化(PSO)加权组合,以提高预测的精度。结果显示,在 2026-2031 年间,大湾区经济增长将保持稳定,但在 2032-2034 年可能出现一定的波动。这一预测为区域政策的制定提供了科学依据,尤其是在应对潜在经济下行时的风险管理措施。
在问题三中,我们运用了相似的建模方法,将粤港澳大湾区与纽约湾区和东京湾区进行对比分析。研究发现,粤港澳大湾区的经济增长活力更强,但波动性也较大;而东京和纽约湾区则表现出更为稳健但增长动力有限的特点。通过对比分析,我们为粤港澳大湾区提出了进一步加强科技投入、区域协同和国际合作的建议,以应对未来经济的不确定性。
总的来说,本文通过多种数学建模方法,对粤港澳大湾区的经济增长进行了深入分析和预测,提出了科学合理的政策建议。创新点在于结合了多种模型进行预测,并通过粒子群优化提高了预测精度,此外还在多个湾区之间进行了对比分析,为大湾区未来发展提供了全面的参考。
关键词:粤港澳大湾区,经济预测,回归分析,机器学习,粒子群优化,区域比较分析
一、符号说明
为了方便我们模型的建立与求解过程 ,我们这里对使用到的关键符号进行以下说明:
| 符号 | 说明 |
| GDP | 国内生产总值,衡量衉港澳大湾区整体经济活动和生产能力 |
| 模型的因变量,表示 GDP 的实际观测值 | |
| 预测的 GDP 值 | |
| X | 自变量矩阵,包括人口、科技、物流、国际环境等影响经济的因责 |
| b | 线性回归模型的系数向量,用于估计各个自变量对 GDP 的影响 |
| 决定系数,用于衡量模型对 GDP 变化的解释能力 | |
| 总平方和,表示所有观测值与均值的偏差的平方和 | |
| 残差平方和,表示预测值与实际值的偏差的平方和 | |
| MAPE | 平均绝对百分比误差,用于评价模型的预测精度 |
| RMSE | 均方根误差,表示模型预测值与实际值之间的平均误差大小 |
| w | 粒子群优化中的权重,用于对不同模型的预测结果进行加权组合 |
| PCA | 主成分分析,用于对国际环境等指标进行降维,减少模型的复杂性 |
| -SNE | t-分布随机邻域嵌入,用于对人口数据降维,探索数据内在结构 |
| 未来预测的时间段,如 5 年或 10 年,代表预测的年限 | |
| ARIMA | 自回归积分滑动平均模型,用于时间序列的 GDP 预测 |
| RF | 随机森林,用于多因毒下的 GDP 预测,利用多棵决策树综合预测 |
| BP NN | 反向传播神经网络,用于基于历史数据的非线性关系建模和预测 |
| PSO | 粒子群优化算法,用于优化模型组合权重,提升预测精度 |
(注:这里只列出论文各部分通用符号,个别模型单独使用的符号在首次引用时会进行说明。)
二、模型的建立与求解
5.1 数据收集处理
5.1.1数据收集与指标概述
为了对粤港澳大湾区及其他湾区经济发展进行科学的定量分析和预测,我们广泛收集了2000年至2024年的多项经济和社会发展指标数据。这些数据来源包括世界银行(World Bank)、国际货币基金组织(IMF)、经济合作与发展组织(OECD)、世界贸易组织(WTO)、联合国贸易和发展会议(UNCTAD)等具有公信力的国际组织,以及知名财经平台和政府统计局,如Statista、Bloomberg、CNBC、美国商务部和各国的统计局等。
图1:数据收集网站示例
具体指标如下所示
对于收集的指标涵盖以下几大方面:
1. 科研
东京研发经费:用于衡量东京湾区在科技创新和研发方面的投入情况。
纽约研发经费:反映纽约湾区的科研发展与投入情况。
粤港澳大湾区科研投入:评估粤港澳大湾区在研发方面的资源配置情况。
2. 物流
东京都物流总量(亿吨):描述东京湾区的物流规模和运输活动。
纽约物流总量(亿吨):用于衡量纽约湾区的物流总量和物流活动的密度。
粤港澳大湾区物流总量(亿吨):展示粤港澳大湾区的物流运作情况,反映区域内的经济活跃度和贸易往来。
3. 人口
东京都人口(百万):描述东京湾区的人口变化趋势。
纽约人口(百万):用于了解纽约湾区的人口规模及其变化情况。
建立了多元回归模型,量化评价了各因素对大湾区 GDP 的影响。通过相关性分析和降维操作,最终找到了影响 GDP 增长最为显著的几个关键因素。结果表明,科技投入和物流网络的完善对大湾区经济的正向影响最大,而人口年龄结构的变化也起到了一定的调节作用。
问题二主要针对未来 5-10 年的经济预测,采用了多种预测模型,包括线性回归、随机森林、BP 神经网络等。各模型的结果经过粒子群优化(PSO)加权组合,以提高预测的精度。结果显示,在 2026-2031 年间,大湾区经济增长将保持稳定,但在 2032-2034 年可能出现一定的波动。这一预测为区域政策的制定提供
5.1.2 数据清洗
对于收集到的数据,首先需要进行必要的数据预处理,我们的数据基本来自于统计年鉴、各种网站。其来源不一定具有真实性,需要对数据进一步处理。主要包括,缺失值处理、时间处理、异常值处理、数据描述性分析。
1、缺失值处理;对于收集的数据中存在的大量缺失值,我们可以选择插值填充。
图1:线性插值图
线性插值是一种基于数据点之间的线性关系来预测缺失值的方法。它假设相邻已知数据点之间的变化是线性的,从而使用这些数据点来估计缺失值。这种方法简单、直观,适合于时间序列数据或具有较强相关性的变量间的缺失值填补。线性插值的基本思想是通过已知的相邻点对缺失值所在的位置进行线性估计,保持数据的整体趋势,尤其适合于在已知数据点之间变化平稳的情形。

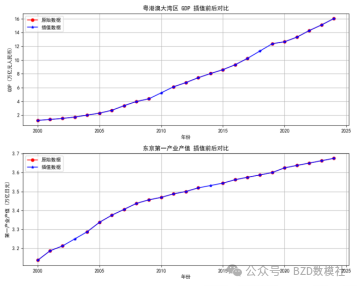
| 该图为python代码绘制结果二 选一即可 |
该图为 matlab代码绘制结果二选一即可 |
异常值处理,对于一直以来飞速发展的经济,24年间存在数据波动,有一定的异常值
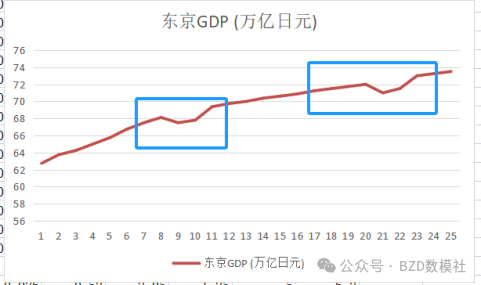
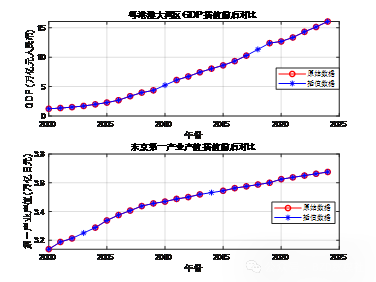
2008年发生的全球金融危机导致了世界各大经济体出现了严重的经济衰退,特别是对金融体系依赖较大的经济区域受到了显著冲击。在图表中可以看到,东京的经济增长在2008至2009年之间表现出一定的波动,这与当时的全球金融市场动荡、资本流动减缓以及进出口贸易下降密切相关。这种经济波动可能体现在当时东京湾区的生产总值数据中,特别是在第一产业方面,由于全球需求的下降,导致产出和收入水平的波动,形成了图表中的异常变化。

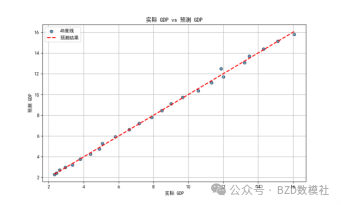
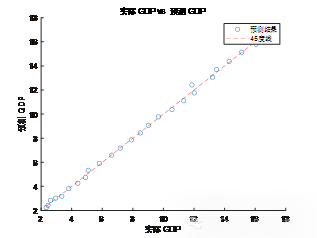
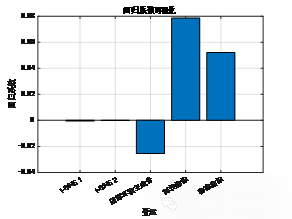
柱状图展示了回归模型中每个变量的回归系数。横轴显示了各个自变量(如 t-SNE 1、t-SNE 2、国际环境主成分、科技指标、物流指标),纵轴为对应的回归系数值。图中可以看到,科技指标和物流指标的系数值较大且为正,表明它们对 GDP 的影响最为显著,且对 GDP 具有正向推动作用。相反,t-SNE 2 的系数为负值,这可能意味着人口结构中的某些方面对 GDP 增长存在抑制作用,而 t-SNE 1 的系数则接近于零,表明它对 GDP 的影响相对较小。总的来说,通过这个柱状图可以直观地看到不同变量在回归模型中的作用大小,帮助我们理解哪些因素对大湾区经济发展起到正面或者负面的影响。
data = xlsread('问题一数据集.xlsx');
% 分割数据
X = data(:, 1:end-1); % 影响因素数据
Y = data(:, end); % GDP数据
% 2. 数据标准化
X_norm = zscore(X);
Y_norm = zscore(Y);
% 3. 主成分分析 (PCA)
[coeff, score, latent, tsquared, explained] = pca(X_norm);
% 可视化主成分贡献率
figure;
pareto(explained);
title('主成分贡献率', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('主成分', 'FontSize', 12);
ylabel('贡献率 (%)', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
% 可视化主成分载荷图(前两个主成分)
% 修改标签以确保它们与输入数据的特征数一致
num_vars = size(X, 2);
var_labels = strcat('因子', string(1:num_vars));
figure;
biplot(coeff(:, 1:2), 'Scores', score(:, 1:2), 'Varlabels', var_labels);
title('主成分载荷图', 'FontSize', 14, 'FontWeight', 'bold');
grid on;
set(gca, 'FontSize', 12);
% 4. 选择前几个主要成分
% 根据贡献率选择前k个成分,假设我们选择前3个成分
k = 3;
X_pca = score(:, 1:k);
% 5. 多元线性回归模型建立
mdl = fitlm(X_pca, Y_norm);
disp(mdl);
% 6. 回归系数可视化
figure;
bar(mdl.Coefficients.Estimate, 'FaceColor', [0.2 0.6 0.5]);
title('回归系数', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('变量', 'FontSize', 12);
ylabel('系数值', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
xlim([0 length(mdl.Coefficients.Estimate) + 1]);
% 7. GDP 预测和结果可视化
Y_pred = predict(mdl, X_pca);
% 可视化实际GDP与预测GDP对比
figure;
plot(1:length(Y_norm), Y_norm, '-o', 'Color', [0 0.4470 0.7410], 'LineWidth', 1.5, 'MarkerSize', 6);
hold on;
plot(1:length(Y_pred), Y_pred, '--s', 'Color', [0.8500 0.3250 0.0980], 'LineWidth', 1.5, 'MarkerSize', 6);
legend('实际GDP', '预测GDP', 'Location', 'Best');
title('实际GDP与预测GDP对比', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('年份', 'FontSize', 12);
ylabel('标准化GDP', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
% 8. 残差分析
figure;
residuals = Y_norm - Y_pred;
plot(1:length(residuals), residuals, '-o', 'Color', [0.4940 0.1840 0.5560], 'LineWidth', 1.5, 'MarkerSize', 6);
title('残差分析', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('年份', 'FontSize', 12);
ylabel('残差', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
% 残差直方图可视化
figure;
histogram(residuals, 'FaceColor', [0.4660 0.6740 0.1880]);
title('残差直方图', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('残差值', 'FontSize', 12);
ylabel('频数', 'FontSize', 12);
grid on;
set(gca, 'FontSize', 12);
原文地址:https://blog.csdn.net/qq_33690821/article/details/143444349
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!