直方图均衡化原理和实现
基本思想
将原始图像的直方图分布转换为一个均匀分布的直方图,这样原图中的高频率亮度值会被展宽,而低频率亮度值则被压缩,从而达到增强图像对比度的效果。
计算过程
假设我们有一个灰度图像,其像素值范围从0到L-1(对于8位图像,L=256)。直方图均衡化的计算步骤如下:
- 计算原始直方图:对于灰度级i,计算图像中灰度级为i的像素数目,记为h(i)。
- 计算累积分布函数(CDF):累积分布函数是直方图的一个累积和,对于灰度级i,CDF计算如下:
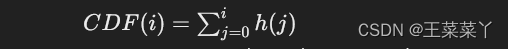
- 归一化CDF:将CDF的值归一化到0到L-1的范围内。这可以通过以下公式完成:
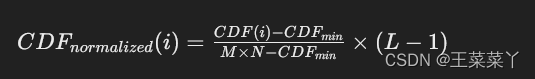
- 应用均衡化映射:最后,对每个像素,使用归一化的CDF值来替换原始图像中的灰度值,这样就得到了均衡化后的图像。
例子
假设图像的像素值如下:
1, 3, 0, 2, 1, 3, 3, 2
- 首先,计算这个图像的直方图。
灰度级: 0 1 2 3
数量: 1 2 2 3
- 计算累积分布函数(CDF)
CDF对于每个灰度级i,累积从0到i的像素数量。因此,对于我们的例子:
灰度级: 0 1 2 3
CDF: 1 3 5 8
- 归一化CDF
将CDF归一化到0到255的范围(对于8位图像)。归一化的公式是:
对于我们的例子,M ×N = 8(图像的像素总数),CDF_{min} = 1(CDF中的最小值),L = 4(灰度级总数)。因此,归一化CDF为:
灰度级: 0 1 2 3
归一化CDF: 0 85 170 255
- 应用均衡化映射
最后,根据归一化的CDF来更新图像的像素值。每个原始像素值i都被映射为归一化CDF中的相应值。因此,原图像像素值转换后为:
原始图像: 1 3 0 2 1 3 3 2
均衡化后: 85 255 0 170 85 255 255 170
由于简化了范围,实际应用中,这些新的像素值将会根据实际情况进行调整,以匹配原图像的灰度级范围。在现实操作中,直方图均衡化后的图像将展现更好的对比度和亮度分布。
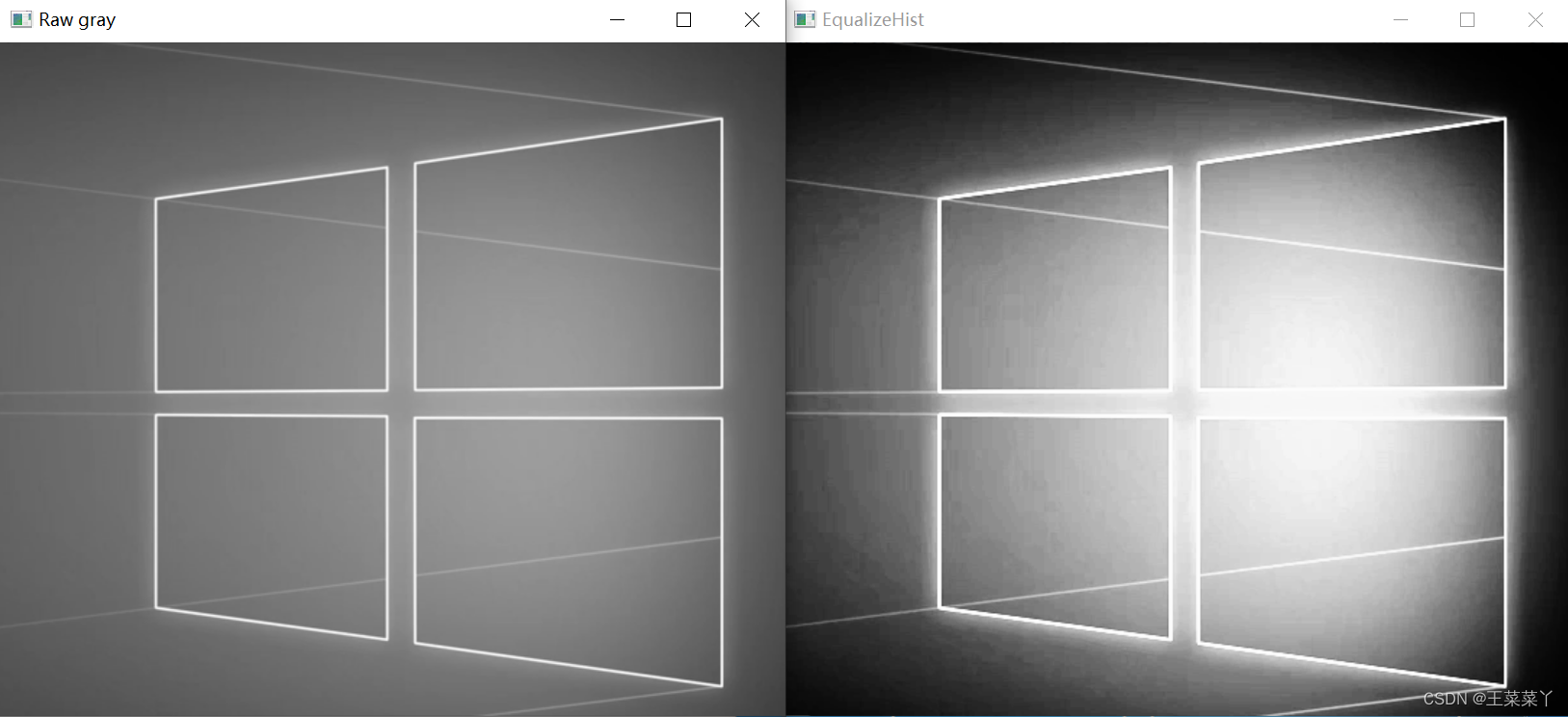
实现1-只针对灰度图像
// 直方图均衡化
void QuickDemo::histogram_eq_demo(Mat &image) {
Mat gray, dst;
cvtColor(image, gray, COLOR_BGR2GRAY);
equalizeHist(gray, dst);
imshow("Raw gray", gray);
imshow("EqualizeHist", dst);
}



原文地址:https://blog.csdn.net/xiaofeixia002X/article/details/136700700
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
