数据结构 第六章（图）【下】

写在前面：

1. 本系列笔记主要以《数据结构（C语言版）》为参考（本章部分图片来源于王道），结合下方视频教程对数据结构的相关知识点进行梳理。所有代码块使用的都是C语言，如有错误欢迎指出。
2. 视频链接：第01周a--前言_哔哩哔哩_bilibili

四、图的应用

1、最小生成树

（1）在一个连通网的所有生成树中，各边的代价（权值）之和最小的那棵生成树称为该连通网的最小代价生成树，简称为最小生成树。

（2）构造最小生成树有多种算法，其中多数算法利用了最小生成树的一种简称为MST的性质：假设N=(V, E)是一个连通网，U是顶点集V的一个非空子集，若(u, v)是一条具有最小权值（代价）的边，其中uϵU（已落在生成树上的顶点集）、vϵV-U（尚未落在生成树上的顶点集），则必存在一棵包含边(u, v)的最小生成树。

（3）普里姆算法：

①算法步骤：

②算法实现：

[1]辅助部分：

struct Closedge
{
VerTexType adjvex;     //最小边在U中的那个顶点
ArcType lowcost;       //最小边上的权值
}closedge[MVNum];     //辅助数组，用来记录从顶点集U到V-U的权值最小的边
int Min(Closedge *U, int n)
{
int min = INT_MAX;
int pos = 0;
for (int i = 0; i < n; ++i) 
{
if (U[i].lowcost != 0 && U[i].lowcost < min) 
{
//U[i].weight != 0 说明不在U中，即V-U
min = U[i].lowcost;
pos = i;
}
}
return pos;
}

[2]核心部分：

void MiniSpanTree_Prim(AMGraph G, VerTexType u)
{
//无向网G以邻接矩阵形式存储，从顶点u触发构造G的最小生成树T，输出T的各条边
int k;   //k为顶点u的下标
for (k = 0; k < G.vexnum; k++)     //确定u在G中的位置，即顶点在G.vexs中的序号
{
if (u == G.vexs[k])
break;
}
for (int j = 0; j < G.vexnum; j++)  //对V-U的每一个顶点初始化
{
if (j != k)
closedge[j] = { u,G.arcs[k][j] };
}
closedge[k].lowcost = 0;      //U集中加入顶点u
for (int i = 1; i < G.vexnum; i++)
{
//选择其余n-1个顶点，生成n-1条边
k = Min(closedge, G.vexnum);  //在V-U中选取权值最小的边
VerTexType u0 = closedge[k].adjvex;  //u0为最小边的一个顶点，属于U
VerTexType v0 = G.vexs[k];           //v0位最小边的另一个顶点，属于V-U
printf("%c->%c ", u0, v0);
closedge[k].lowcost = 0;      //第k个顶点并入U集
for (int j = 0; j < G.vexnum; j++)
{
if (G.arcs[k][j] < closedge[j].lowcost)  //新顶点并入U后重新选择最小边
closedge[j] = { G.vexs[k],G.arcs[k][j] };
}
}
}

③普里姆算法的时间复杂度为O(n2)，与网中的边数无关，因此适用于求稠密网的最小生成树。

（4）克鲁斯卡尔算法：

①算法步骤：

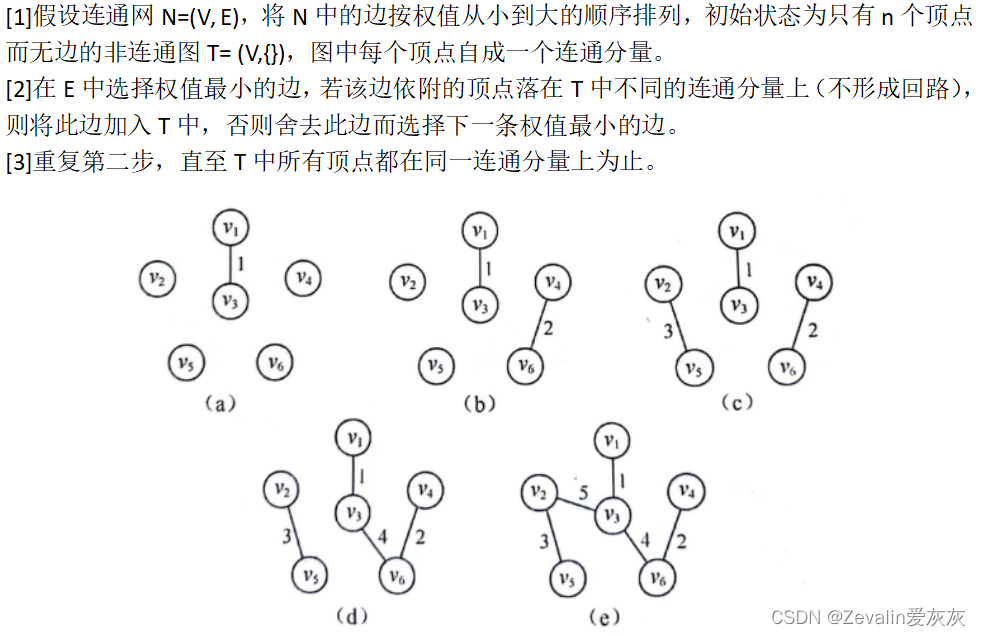
②算法实现：

[1]辅助部分：

struct Edge
{
VerTexType Head;       //边的始点
VerTexType Tail;       //边的终点
ArcType lowcost;       //边上的权值
}edge[MVNum];         //存储边的信息
int Vexset[MVNum];    //辅助数组

void Sort(Edge *E, int length)   //采用冒泡排序将数组edge中的元素按权值从小到大排序
{
bool flag = true; //排序flag
for (int i = 0; i < length - 1 && flag; ++i)  //如果未发生交换则说明有序
{ 
flag = false; //第一次设置为false，若某轮循环结束后标志仍为false，说明排序可以结束
for (int j = 0; j < length - 1 - i; ++j) 
{
if (E[j].lowcost > E[j + 1].lowcost) 
{
flag = true; //如果发生交换，标志为true
Edge temp = E[j];
E[j] = E[j + 1];
E[j + 1] = temp;
}
}
}
}

[2]核心部分：

void MiniSpanTree_Kruskal(AMGraph G)
{
//无向网G以邻接矩阵形式存储，构造G的最小生成树T，输出T的各条边
Edge *edge = (Edge*)malloc(sizeof(Edge) * G.arcnum);  //为G建立Edge数组
Edge *p = edge;
for (int i = 0; i < G.vexnum; i++) //初始化Edge数组（无向图遍历邻接矩阵的上三角即可）
{
for (int k = i + 1; k < G.vexnum; k++)
{
if (G.arcs[i][k] < MaxInt)
{
p->Head = G.vexs[i];
p->Tail = G.vexs[k];
p->lowcost = G.arcs[i][k];
p++;
}
}
}
Sort(edge, G.arcnum);   //Edge中的元素按权值升序排序
for (int i = 0; i < G.arcnum; i++)
Vexset[i] = i;   //辅助数组，表示各顶点自成一个连通分量
for (int i = 0; i < G.arcnum; i++)
{
int v1, v2;
for (v1 = 0; v1 < G.vexnum; v1++)      //v1为边的始点Head的下标
if (edge[i].Head == G.vexs[v1])
break;
for (v2 = 0; v2 < G.vexnum; v2++)      //v2为边的终点Tail的下标
if (edge[i].Tail == G.vexs[v2])
break;
int vs1 = Vexset[v1];   //获取边edge[i]的始点所在的连通分量vs1
int vs2 = Vexset[v2];   //获取边edge[i]的终点所在的连通分量vs2
if (vs1 != vs2)   //边的两个顶点分属不同的连通分量
{
printf("%c->%c ", edge[i].Head, edge[i].Tail);  //输出此边
for (int j = 0; j < G.vexnum; j++)  //合并vs1和vs2两个分量，两个集合统一编号
if (Vexset[j] == vs2)
Vexset[j] = vs1;   //集合编号为vs2的都改为vs1
}
}
}

③克鲁斯卡尔算法的时间复杂度为，与网中的边数有关。与普里姆算法相比，克鲁斯卡尔算法更适合于求稀疏网的最小生成树。

2、最短路径

（1）在带权有向网中，习惯上称路径上的第一个顶点为源点，最后一个顶点为终点。

（2）求从某个源点到其余各顶点的最短路径——迪杰斯特拉算法：

①算法思路：

②算法步骤：

③算法实现：

void ShortestPath_DIJ(AMGraph G, int v0, int* path)
{
//用Dijkstra算法求有向网的v0顶点到其余顶点的最短路径
int n = G.vexnum;    //G中顶点个数
int v;
bool* S = (bool*)malloc(sizeof(bool)*n);
ArcType* D = (ArcType*)malloc(sizeof(ArcType)*n);
for (v = 0; v < n; v++)
{
S[v] = false;           //S初始为空集
D[v] = G.arcs[v0][v];   //将v0到各个终点的最短路径长度初始化为弧上的权值
if (D[v] < MaxInt)
path[v] = v0;   //v0和v之间有弧，v的前驱置为v0
else
path[v] = -1;   //v0和v之间无弧，v的前驱置为-1
}
S[v0] = true;    //将v0加入S
D[v0] = 0;       //源点到源点的距离为0
for (int i = 1; i < n; i++)
{
int min = MaxInt;
for (int j = 0;j < n;j++)
if (!S[j] && D[j] < min)
{
v = j;
min = D[j];
}  //选择一条当前的最短路径，终点为v
S[v] = true;   //将v加入S
for (int j = 0;j < n;j++)  //更新从v0出发到集合V-S上所有顶点的最短路径长度
if (!S[j] && (D[v] + G.arcs[v][j] < D[j]))
{
D[j] = D[v] + G.arcs[v][j];  //更新D[j]
path[j] = v;                 //更新j的前驱为v
}
}
}

④该算法的时间复杂度为O()。

⑤举例：

[1]对六个顶点依次初始化，结果如下：

v	0	1	2	3	4	5
S	true	false	false	false	false	false
D	0	∞	10	∞	30	100
Path	-1	-1	0	-1	0	0

[2]从到各终点的最短路径长度D和最短路径的求解过程：

（3）求每一对顶点之间的最短路径——弗洛伊德算法：

①算法思路：逐个顶点试探，从到的所有可能存在的路径中选出一条长度最短的路径。

②算法步骤：

③算法实现：

void ShortestPath_Floyd(AMGraph G, int** path)
{
//用Floyd算法求有向网G中各对顶点i和j之间的最短路径
bool* S = (bool*)malloc(sizeof(bool)*G.vexnum);
ArcType** D = (ArcType**)malloc(sizeof(ArcType*)*G.vexnum);
for (int i = 0; i < G.vexnum; i++)
{
D[i] = (ArcType*)malloc(sizeof(ArcType)*G.vexnum);
}
for (int i = 0; i < G.vexnum; i++)  //初始化n阶方阵
{
for (int j = 0; j < G.vexnum; j++)
{
D[i][j] = G.arcs[i][j];
if (D[i][j] < MaxInt && i != j)
path[i][j] = i;  //i和j之间有弧，j的前驱置为i
else
path[i][j] = -1; //i和j之间无弧，j的前驱置为-1
}
}
for (int k = 0; k < G.vexnum; k++)
for (int i = 0; i < G.vexnum; i++)
for (int j = 0; j < G.vexnum; j++)
if (D[i][k] + D[k][j] < D[i][j])
{  //从i经k到j的一条路径更短，更新D[i][j]和j的前驱
D[i][j] = D[i][k] + D[k][j];
path[i][j] = path[k][j];
}
}

④该算法的时间复杂度为O()。

⑤举例：

3、拓扑排序

（1）AOV—网：

（2）拓扑排序的过程：

（3）拓扑排序算法实现：

Status TopologicalSort(ALGraph G, int topo[])
{
//有向图G采用邻接表作为存储结构
//若G无回路，则生成G的一个拓扑序列topo并返回OK，否则返回ERROR
int *indegree = (int*)malloc(sizeof(int)*G.vexnum);  //存储所有顶点的入度的数组
memset(indegree, 0, sizeof(int)*G.vexnum);    //初始化indegree数组，各顶点入度为0
for (int i = 0; i < G.vexnum; ++i)   //分别对每个顶点求入度
{
ArcNode *p = G.vertices[i].firstarc;  //指向首个邻接点
while (p)
{
indegree[p->adjvex]++;  //入度+1
p = p->nextarc;    //指向下一个邻接点
}
}
SqStack S;
InitStack(&S);    //栈S初始化为空
for (int i = 0; i < G.vexnum; i++)  //入度为0者进栈
if (!indegree[i])
Push(&S, i);
int m = 0;   //对输出顶点计数
while (!StackEmpty(S))
{
int i;
Pop(&S, &i);   //使栈顶顶点vi出栈
topo[m] = i;   //将顶点vi保存在拓扑序列数组topo中
m++;           //输出顶点数+1
ArcNode *p = G.vertices[i].firstarc;  //指向vi的第一个邻接点
while (p)
{
int k = p->adjvex;  //vk为vi的邻接点
indegree[k]--;      //vi的每个邻接点的入度-1
if (indegree[k] == 0)  //入度减为0，入栈
Push(&S, k);
p = p->nextarc;     //指向下一个邻接点
}
}
if (m < G.vexnum) return ERROR;
else return OK;
}

（4）有向无环图可以用于描述表达式，因为运算符有不同的优先级，需要完成高优先级的运算才能接着完成低优先级的运算。

4、关键路径

（1）AOE—网：

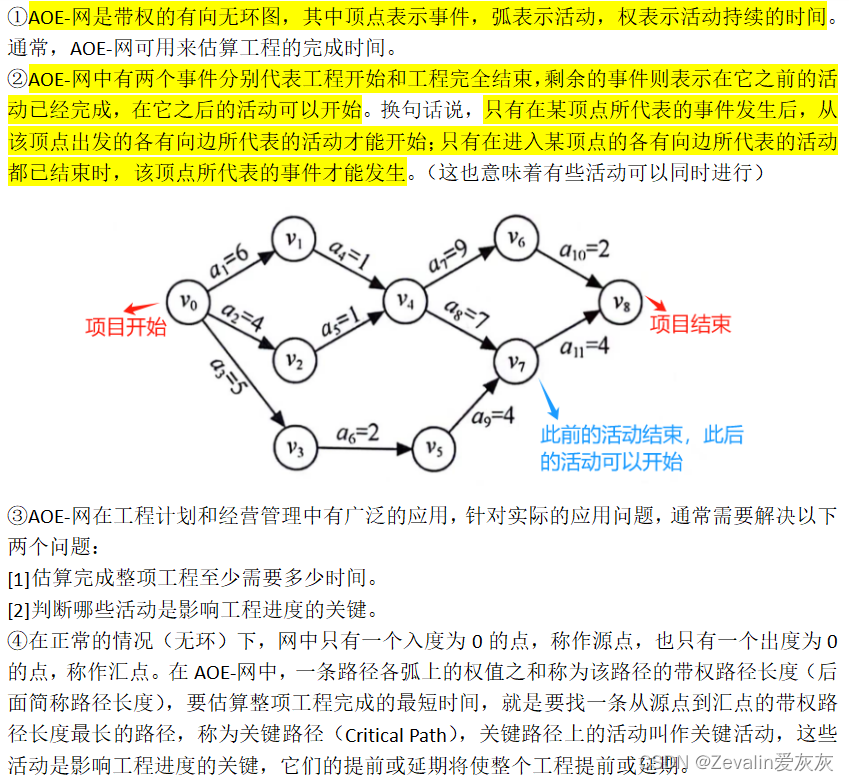
（2）关键路径求解过程：

①首先定义4个描述量：

②一个活动的最迟开始时间l(i)和其最早开始时间e(i)的差值是该活动完成的时间余量，它是在不增加完成整个工程所需的总时间的情况下，活动可以拖延的时间。当一活动的时间余量为0时，说明该活动必须如期完成，否则就会拖延整个工期，所以称l(i)-e(i)=0的活动是关键活动。

③对图中顶点进行排序，在排序过程中按拓扑序列求出每个事件的最早发生时间ve(i)。

④按逆拓扑序列求出每个事件的最迟发生时间vl(i)。

⑤求出每个活动的最早开始时间e(i)。

⑥求出每个活动的最晚开始时间(i)。

⑦找出e(i)=l(i)的活动，即关键活动，由关键活动形成的由源点到汇点的每一条路径就是关键路径（关键路径有可能不止一条）。

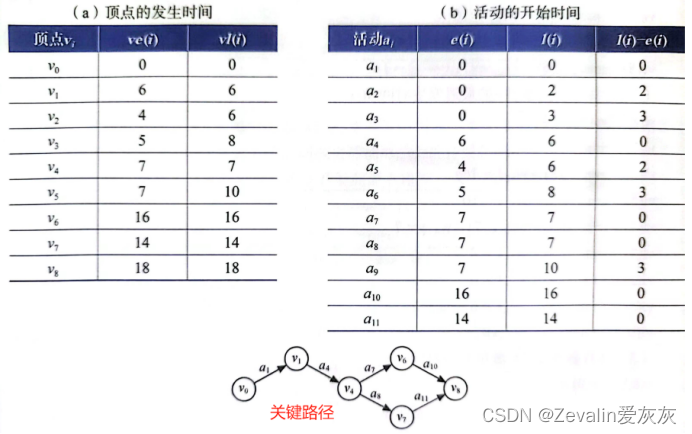
（3）关键路径算法实现：

Status CriticalPath(ALGraph G)
{
//G为邻接表存储的有向网，输出G的各项关键活动
int *topo = (int*)malloc(sizeof(int)*G.vexnum);
if (TopologicalSort(G, topo) == OK)  //拓扑排序检查是否存在有向环，获取拓扑序列
return ERROR;
int *ve = (int*)malloc(sizeof(int*)*G.vexnum);
int *vl = (int*)malloc(sizeof(int*)*G.vexnum);
for (int i = 0; i < G.vexnum; i++)
ve[i] = 0;  //给每个事件的最早发生时间置初值0
/*按拓扑次序求每个事件的最早发生时间*/
for (int i = 0; i < G.vexnum; i++)
{
int k = topo[i];  //取得拓扑序列中的顶点序号k
ArcNode* p = G.vertices[k].firstarc;  //指向k的第一个邻接点
while (p)
{
int j = p->adjvex;  //邻接顶点的序号
if (ve[j] < ve[k] + p->info)  //更新顶点j的最早发生时间ve[j]
ve[j] = ve[k] + p->info;
p = p->nextarc;   //指向k的下一个邻接点
}
}
for (int i = 0; i < G.vexnum; i++)
vl[i] = ve[G.vexnum - 1];  //给每个事件的最迟发生时间置初值ve[n-1]
    /*按逆拓扑次序求每个事件的最晚发生时间*/
for (int i = G.vexnum - 1; i >= 0; i--)
{
int k = topo[i];  //取得拓扑序列中的顶点序号k
ArcNode* p = G.vertices[k].firstarc;  //指向k的第一个邻接点
while (p)
{
int j = p->adjvex;  //邻接顶点的序号
if (vl[k] < vl[j] + p->info)  //更新顶点k的最迟发生时间vl[k]
vl[k] = vl[j] + p->info;
p = p->nextarc;   //指向k的下一个邻接点
}
}
/*判断每一活动是否为关键活动*/
for (int i = 0; i < G.vexnum; i++)
{
ArcNode* p = G.vertices[i].firstarc;  //指向i的第一个邻接点
while (p)
{
int j = p->adjvex;  //邻接顶点的序号
int e = ve[i];           //计算活动的最早开始时间
int l = vl[j] - p->info; //计算活动的最晚开始时间
if (e == l)   //若为关键活动，输出之
printf("%d-%d ", G.vertices[i].data, G.vertices[i].data);
p = p->nextarc;   //指向i的下一个邻接点
}
}
}

（4）使用该算法的注意事项：

①若网中有几条关键路径，则需加快同时在几条关键路径上的关键活动。

②如果一个活动处于所有的关键路径上，那么提高这个活动的速度就能缩短整个工程的完成时间。

③处于所有的关键路径上的活动完成时间缩短太多的话，可能会使原来的关键路径变为非关键路径，这时需要重新寻找关键路径。

五、算法设计举例

1、例1

（1）问题描述：分别以邻接矩阵和邻接表作为存储结构，实现无向网（使用邻接矩阵）/无向图（使用邻接表）的几个基本操作，分别为增加一个新顶点、删除一个顶点及其相关的边、增加一条边和删除一条边。

（2）代码：

①邻接矩阵部分：

Status InsertVex(AMGraph &G, VerTexType v)  //增加一个新顶点v
{
if (G.vexnum == MVNum)
return OVERFLOW;    //顶点数已达最大值
G.vexs[G.vexnum] = v;
for (int i = 0; i <= G.vexnum; i++)  //仅增加顶点，不增加与其相关的边
{
G.arcs[i][G.vexnum] = MaxInt;
G.arcs[G.vexnum][i] = MaxInt;
}
G.vexnum++;  //当前顶点数+1
return OK;
}

Status DeleteVex(AMGraph &G, VerTexType v)  //删除顶点v及其相关的边
{
if (G.vexnum == 0)
return ERROR;   //没有顶点可删
int i;
for (i = 0; i < G.vexnum; i++)  //找到顶点v所在位置
{
if (G.vexs[i] == v)
break;
}
if (i != G.vexnum)  //如果顶点v存在于图G中，可以进行删除（逻辑删除）
{
VerTexType tmp = G.vexs[i];
G.vexs[i] = G.vexs[G.vexnum - 1];
G.vexs[G.vexnum - 1] = tmp;  //vexs中最后一个顶点与预删除顶点v互换存储位置
for (int j = 0; j < G.vexnum; j++)  //矩阵中最后一个顶点与预删除顶点v的相关边互换存储位置
{
ArcType tmp = G.arcs[i][j];
G.arcs[i][j] = G.arcs[G.vexnum - 1][j];
G.arcs[G.vexnum - 1][j] = tmp;
tmp = G.arcs[j][i];
G.arcs[j][i] = G.arcs[j][G.vexnum - 1];
G.arcs[j][G.vexnum - 1] = tmp;
}
for (int j = 0; j < G.vexnum; j++)  //如果是针对有向图的操作，则需要二维遍历
{
if (G.arcs[j][G.vexnum - 1] != MaxInt)  //如果逻辑删除的边不是无穷大（也就是存在）
G.arcnum--;  //边总数-1
}
G.vexnum--;  //顶点总数-1
return OK;
}
else
return ERROR;
}

Status InsertArc(AMGraph &G, VerTexType v, VerTexType w, ArcType t)  //增加一条边<v,w>
{
int i, j;
for (i = 0; i < G.vexnum; i++)  //需要顶点v在G中存在，并找到其下标
{
if (G.vexs[i] == v)
break;
}
for (j = 0; j < G.vexnum; j++)  //需要顶点w在G中存在，并找到其下标
{
if (G.vexs[j] == w)
break;
}
if (i != G.vexnum && j != G.vexnum && i != j && G.arcs[i][j] != MaxInt)  //该边需要不存在才能增加
{
G.arcs[i][j] = t;
G.arcs[j][i] = t;
G.arcnum++;   //边总数+1
return OK;
}
else
return ERROR;
}

Status DeleteArc(AMGraph &G, VerTexType v, VerTexType w)  //删除一条边<v,w>
{
int i, j;
for (i = 0; i < G.vexnum; i++)  //需要顶点v在G中存在，并找到其下标
{
if (G.vexs[i] == v)
break;
}
for (j = 0; j < G.vexnum; j++)  //需要顶点w在G中存在，并找到其下标
{
if (G.vexs[j] == w)
break;
}
if (i != G.vexnum && j != G.vexnum && i != j && G.arcs[i][j] != MaxInt)  //该边需要存在才能删除
{
G.arcs[i][j] = MaxInt;
G.arcs[j][i] = MaxInt;
G.arcnum--;    //边总数-1
return OK;
}
else
return ERROR;
}

②邻接表部分：

Status InsertVex(ALGraph &G, VerTexType v)  //增加一个新顶点v
{
if (G.vexnum == MVNum)
return OVERFLOW;    //顶点数已达最大值
G.vertices[G.vexnum].data = v;
G.vertices[G.vexnum].firstarc = NULL;  //仅增加顶点，不增加与其相关的边
G.vexnum++;  //当前顶点数+1
return OK;
}

Status DeleteVex(ALGraph &G, VerTexType v)  //删除顶点v及其相关的边
{
if (G.vexnum == 0)
return ERROR;   //没有顶点可删
int i;
for (i = 0; i < G.vexnum; i++)  //找到顶点v所在位置
{
if (v == G.vertices[i].data)
break;
}
if (v != G.vexnum)  //如果顶点v存在于图G中，可以进行删除（物理删除）
{
ArcNode* p = G.vertices[i].firstarc;
int num = 0;
while (p)
{
ArcNode* q1 = p;
p = p->nextarc;
ArcNode* q2 = G.vertices[q1->adjvex].firstarc;
ArcNode* q3 = q2;
if (q2->adjvex == i)
{
G.vertices[q1->adjvex].firstarc = q2->nextarc;
free(q3);
num++;
}
else
{
q2 = q2->nextarc;
while (q2)
{
if (q2->adjvex == G.vexnum - 1)
{
q2->adjvex = i;
}
else if (q2->adjvex == i)
{
ArcNode* q4 = q2;
q3->nextarc = q2->nextarc;
free(q4);
num++;
break;
}
q2 = q2->nextarc;
}
}
free(q1);
}
VNode tmp = G.vertices[i];
G.vertices[i] = G.vertices[G.vexnum - 1];
G.vertices[G.vexnum - 1] = tmp;
G.vexnum--;   //顶点总数-1
G.arcnum = G.arcnum - num / 2;  //如果是针对有向图的操作，num不需要除以2
return OK;
}
else
return ERROR;
}

Status InsertArc(ALGraph &G, VerTexType v, VerTexType w)  //增加一条边<v,w>
{
int i, j;
for (i = 0; i < G.vexnum; i++)  //需要顶点v在G中存在，并找到其下标
{
if (v == G.vertices[i].data)
break;
}
for (j = 0; j < G.vexnum; j++)
{
if (w == G.vertices[j].data)  //需要顶点w在G中存在，并找到其下标
break;
}
if (i == G.vexnum || i == G.vexnum)
return ERROR;
ArcNode* p1 = (ArcNode*)malloc(sizeof(ArcNode));
p1->adjvex = j;
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1;
ArcNode* p2 = (ArcNode*)malloc(sizeof(ArcNode));
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p2;
G.arcnum++;  //边总数+1
return OK;
}

Status DeleteArc(ALGraph &G, VerTexType v, VerTexType w)  //删除一条边<v,w>
{
int i, j;
for (i = 0; i < G.vexnum; i++)  //需要顶点v在G中存在，并找到其下标
{
if (v == G.vertices[i].data)
break;
}
for (j = 0; j < G.vexnum; j++)  //需要顶点w在G中存在，并找到其下标
{
if (w == G.vertices[j].data)
break;
}
if (i == G.vexnum || i == G.vexnum)
return ERROR;
if (G.vertices[i].firstarc->adjvex == w)
{
ArcNode* p = G.vertices[i].firstarc;
G.vertices[i].firstarc = G.vertices[i].firstarc->nextarc;
free(p);
}
else
{
ArcNode* p1 = G.vertices[i].firstarc;
ArcNode* p2 = G.vertices[i].firstarc;
while (p2->nextarc)
{
if (p2->nextarc)
{
p1->nextarc = p2->nextarc;
break;
}
p1 = p2;
p2 = p2->nextarc;
}
}
if (G.vertices[j].firstarc->adjvex == v)
{
ArcNode* p = G.vertices[j].firstarc;
G.vertices[j].firstarc = G.vertices[j].firstarc->nextarc;
free(p);
}
else
{
ArcNode* p1 = G.vertices[j].firstarc;
ArcNode* p2 = G.vertices[j].firstarc;
while (p2->nextarc)
{
if (p2->nextarc)
{
p1->nextarc = p2->nextarc;
break;
}
p1 = p2;
p2 = p2->nextarc;
}
}
G.arcnum--;  //边总数-1
return OK;
}

2、例2

（1）问题描述：设计一个算法，求图G中距离顶点v的最短路径长度最大的一个顶点，设v可达其余各个顶点。

（2）代码：

int T1(AMGraph G, int v0)
{
int n = G.vexnum;           //n为G中顶点的个数
bool S[MVNum];
int D[MVNum];
int Path[MVNum];
int v;
for (v = 0; v < n; v++)     //n个顶点依次初始化
{
S[v] = false;           //S初始为空集
D[v] = G.arcs[v0][v];   //将v0到各个终点的最短路径长度初始化为弧上的权值
if (D[v] != 0)
D[v] = MaxInt;
if (D[v] < MaxInt)
Path[v] = v0;      //如果v0和v之间有弧，则将v的前驱置为v0
else
Path[v] = -1;      //如果v0和v之间无弧，则将v的前驱置为-1
}
S[v0] = true;              //将v0加入S
D[v0] = 0;                 //源点到源点的距离为0
//初始化结束，开始主循环，每次求得v0到某个顶点v的最短路径，将v加到S集
for (int i = 1; i < n; i++)       //对其余n-1个原点依次进行计算
{
int min = MaxInt;
for (int w = 0; w < n; w++)
{
if (!S[w] && D[w] < min)
{
v = w;
min = D[w];           //选择一条当前的最短路径，终点为v
}
}
S[v] = true;                  //将v加入S
for (int w = 0; w < n; w++)   //更新从v0出发到集合V-S上所有顶点的最短路径长度
{
if (!S[w] && (D[v] + G.arcs[v][w] < D[w]))
{
D[w] = D[v] + G.arcs[v][w];    //更新D[w]
Path[w] = v;                   //更改w的前驱为v
}
}
}
//最短路径求解完毕，设距离顶点v0的最短路径长度最大的一个顶点为m
int Max = D[0];
int m = 0;
for (int i = 1; i < n; i++)
if (Max < D[i]) m = i;
return m;                      //返回顶点下标
}

3、例3

（1）问题描述：一个连通图采用邻接表作为存储结构，设计一个算法，实现从顶点v出发的深度优先遍历的非递归过程。

（2）代码：

void T2(ALGraph G, int v)
{
SqStack S;
InitStack(&S);              //构造一个空栈
Push(&S, v);                //顶点v进栈
while (!StackEmpty(S))
{
int k;
Pop(&S, &k);            //栈顶元素k出栈
if (!visited_AL[k])
{
printf("%c ", k);   //访问第k个节点
visited_AL[k] = true;
ArcNode* p = G.vertices[k].firstarc;   //p指向k的边链表的第一个边节点
while (p != NULL)                      //边节点非空
{
int w = p->adjvex;
if (!visited_AL[w])                //如果k的邻接点未访问，则进栈
Push(&S, w);
p = p->nextarc;
}
}
}
}

4、例4

（1）问题描述：基于图的深度优先搜索策略设计一算法，判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径（i≠j）。

（2）代码：

bool T3(ALGraph G, int i, int j)
{
if (i == j)       //首尾相遇，说明存在路径，递归结束
return true;
else
{
visited_AL[i] = true;    //访问第v个顶点，并置访问标志数组相应分量值为true
ArcNode* p = G.vertices[i].firstarc;   //p指向v的边链表的第一个边节点
while (p != NULL)         //边节点非空
{
int w = p->adjvex;    //w是v的邻接点
p = p->nextarc;       //p指向下一个边节点
if (!visited_AL[w] && T3(G, w, j))
return true;
}
}
return false;
}

5、例5

（1）问题描述：采用邻接表存储结构，设计一个算法，判别无向图中任意给定的两个顶点之间是否存在一条长度为k的简单路径。

（2）代码：

bool T4(ALGraph G, int i, int j, int k)
{
if (i == j && k == 0)         //找到符合要求的路径，递归结束
return true;
else if (k > 0)
{
visited_AL[i] = true;     //访问第v个顶点，并置访问标志数组相应分量值为true
ArcNode* p = G.vertices[i].firstarc;   //p指向v的边链表的第一个边节点
while (p != NULL)         //边节点非空
{
int w = p->adjvex;    //w是v的邻接点
p = p->nextarc;       //p指向下一个边节点
if (!visited_AL[w] && T4(G, w, j, k - 1))
return true;
}
visited_AL[i] = false;    //允许曾经被访问过的节点出现在另一条路径中
}
return false;
}

原文地址：https://blog.csdn.net/Zevalin/article/details/137401348

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！