世界的本质是旋转(6)-在复平面上借助软件无线电SDR解调BPSK波形

🕗 发布于 2024-03-05 13:18 复平面 BPSK C语言解调软件无线电

在上一篇文章中，已经完成了BPSK波形的发射。

相对于BPSK波形的生成总共就4行代码，接收要略微复杂一些，算上各种同步、锁相环，约80行。完整版参考Git仓库，这里给出其C语言核心代码如下：

vector<char> demod_psk(const short (*iqdata)[2], const int splen)
{
static const double fir_rcos_q25[25] = {-0.018773,0.0030136,0.032677,0.047094,0.02655,-0.027522,-0.085225,-0.099447,-0.032147,0.11904,0.31118,0.472,0.53463,0.472,0.31118,0.11904,-0.032147,-0.099447,-0.085225,-0.027522,0.02655,0.047094,0.032677,0.0030136,-0.018773};
static double fir_cache_i[25] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
static double fir_cache_q[25] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
//fir filter
static unsigned long long clk = 0, bad_angle = 0, last_synclk = 0;
static const int WINSZ = 4000;
static double stati_win[WINSZ][2], sum_win[2] = {0,0};
static double cache_win[WINSZ][2];
//smp best pos
static double clk_offset[4] = {0,0,0,0};
static bool bInited = false;
static double curr_dp = 0;
static int bestOff = 0;
//stati_win，cache_win 归零初始化略去
//...
//bpsk bit out
vector<char> dp_bitbuf；
//逐个点步进
for (int i=0;i<splen;++i)
{
//1. 滤波去带外噪声
fir_cache_i[clk % 25] = iqdata[i][0];
fir_cache_q[clk % 25] = iqdata[i][1];
double fval_i = 0,fval_q = 0;
for (int f=0;f<25;++f){
fval_i += fir_cache_i[(clk+f+1)  % 25] * fir_rcos_q25[f];
fval_q += fir_cache_q[(clk+f+1)  % 25] * fir_rcos_q25[f];
}
//2. 窗口统计去直流分量
sum_win[0] -= stati_win[clk%WINSZ][0];
sum_win[1] -= stati_win[clk%WINSZ][1];
sum_win[0] += fval_i;
sum_win[1] += fval_q;
stati_win[clk%WINSZ][0] = fval_i;
stati_win[clk%WINSZ][1] = fval_q;
const double dcremoved[2] {fval_i - sum_win[0]/WINSZ, fval_q - sum_win[1]/WINSZ };
cache_win[clk%WINSZ][0] = dcremoved[0];
cache_win[clk%WINSZ][1] = dcremoved[1];
//3. 最佳采样位置跟踪
const int curr_offv = clk % 4;
clk_offset[curr_offv] += (dcremoved[0]*dcremoved[0] + dcremoved[1] * dcremoved[1]); //符号时钟位置同步
double phy = 0;//锁相环误差
if (curr_offv == bestOff)
{
//锁相旋转
double rt[2]{cos(-curr_dp),sin(-curr_dp)};
const double out[2]{cache_win[(clk+4)%WINSZ][0],cache_win[(clk+4)%WINSZ][1]};
double rp[2]{
out[0] * rt[0] - out[1] * rt[1],
out[0] * rt[1] + out[1] * rt[0]
};
//失锁重置，即重新测量相位误差
phy = atan_r(rp[1],rp[0]);
if (phy >= c_pi/4 || phy <=-c_pi/4)
{
curr_dp = atan_r(out[1],out[0]);
rt[0] = cos(-curr_dp);
rt[1] = -sin(curr_dp);
rp[0] = out[0] * rt[0] - out[1] * rt[1];
rp[1] = out[0] * rt[1] + out[1] * rt[0];
phy = atan_r(rp[1],rp[0]);
++bad_angle;
}
//更新环路
curr_dp += (phy/2);
curr_dp =wrapto2pi(curr_dp );
//解调后的01比特
dp_bitbuf.push_back( rp[0] < 0? 0: 1 );
}
//错开最佳点2符号进行时钟误差补偿
if (last_synclk + WINSZ < clk && ((clk+2) % 4)==bestOff)
{
last_synclk = clk;
int maxo = 0;
double maxv = clk_offset[0];
if (clk_offset[1] > maxv) { maxo = 1; maxv = clk_offset[1];}
if (clk_offset[2] > maxv) { maxo = 2; maxv = clk_offset[2];}
if (clk_offset[3] > maxv) { maxo = 3; maxv = clk_offset[3];}
bestOff = maxo;
clk_offset[0] = 0;clk_offset[1] = 0;
clk_offset[2] = 0;clk_offset[3] = 0;
}
++clk;
}

return dp_bitbuf；
}

不停地调用上述代码，输入一段一段接收到的X\Y坐标（IQ路信号），输出一串串01比特。上述代码采用全静态内存、无任何的搬移、拷贝，基本满足一般低速信号的处理要求。

下面我们逐一介绍每一步干了什么。在此之前，先讨论一个题外话。

0. 题外话：软硬件的思维大不相同

先放一张图：

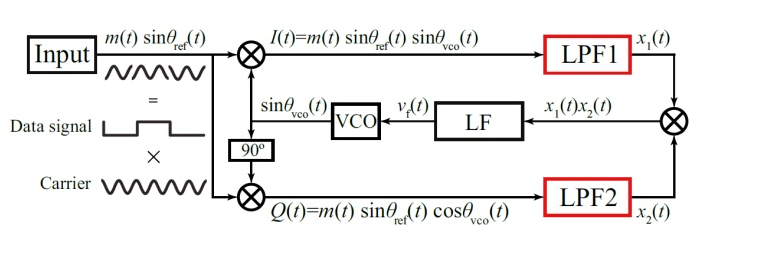
有多少人在看到这个BPSK 科斯塔斯环时，会思考这个东西的C语言如何实现VCO、LF、LPF，这么多滤波如何提速等等。其实我也困扰了很久.，其实若从复平面、X\Y坐标去理解，会发现用PC计算机实现BPSK解调，完全不必有VCO以及这些设施。

上面的示意图，是在上个世纪使用模拟器件处理解调工作的最佳方案。硬件记不住太多的历史数据，因此无法统计一些信息；硬件无法方便的计算各种角度，比如atan。所以它用一个压控震荡源产生一个对消载波，去环路匹配残差频率。在C语言里，我们可以直接测量角度，从而跟踪上向量的旋转，对消载波是不必要的。PC的思路是：

符号时刻t0，观察到向量(x,y)在131度，对BPSK，则下一个符号时刻 t1 要么是 131+180,要么还是131度。因此，直接测量 atan(y,x）,而后稍微和预计位置比较一下，就可以得到残差相位了，太直接了。整个环路就等效为一个角度变量的跟踪。

旋转打地鼠

如果把接收BPSK的两个可能的符号位置想象成一个黑色幕布下的两组地鼠洞，地鼠会随时从任意洞口钻出来。更要命的是，整个地鼠机放在一个转台上，转台的转速就是各级模拟/数字下变频（ADC、DDC）到0频（基带，或者复平面xy坐标）时保留的频率误差。现在，要准确的打地鼠，就是和解调非常类似的活动。

按照4倍速率XY坐标运动的地鼠	角度跟踪最佳状态的地鼠

传统教材的科斯塔斯环，等于是要产生一个和残差相位相反的旋转矢量，叠加到输入载波，让整体的地鼠盘子不动。而我们的C语言解调，只要测量当前的残差相位，并不断跟踪即可。盘子继续转动，多了一个测量杆子（curr_dp）,这个杆子和地鼠一起转动，每次根据地鼠的位置，跟踪调整杆子的角度即可。

1. 滤波去带外噪声

由于要进行时钟同步，以及奈奎斯特限制，接收时往往采用比发射速率高几倍的速率进行接收。此时，信号带宽外的噪声也进来了。去除带外噪声，可以一定程度良化波形。

上文的代码：

//1. 滤波去带外噪声
fir_cache_i[clk % 25] = iqdata[i][0];
fir_cache_q[clk % 25] = iqdata[i][1];
double fval_i = 0,fval_q = 0;
for (int f=0;f<25;++f){
fval_i += fir_cache_i[(clk+f+1)  % 25] * fir_rcos_q25[f];
fval_q += fir_cache_q[(clk+f+1)  % 25] * fir_rcos_q25[f];
}

构造了一个环形结构，实现时域滤波的卷积计算。由于FIR是对称的，导致卷积反转不再需要。只要用时钟咬紧当前的位置即可，搞一个25长度的环状缓存，只记忆滤波需要的部分。同时，时钟推进后，用取余替代memcpy，不进行内存搬移，几乎没有开销。

这部分的效果，可以通过等效的Octave代码处理真实数据来展示：
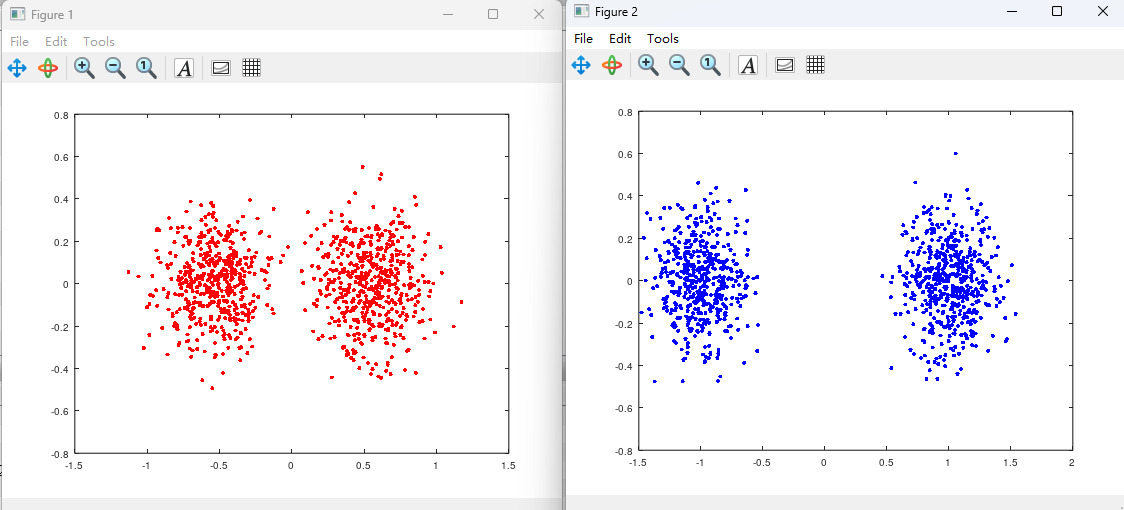filter 左图是滤波前的向量位置打点图，右图是滤波后的。显然滤波后，0、1两坨坐标分的更开了。下面是仿真代码：

pkg load communications;
clear;
clc;
mulrate = 4;
symlen = 1000;
dta1_bits = randint (1, symlen, 2);
dta2_symbols = pskmod (dta1_bits, 2, 0, "gray");
#dta2_symbols = qammod (dta1_bits, 4);
#figure(); plot (dta2_symbols, "bx");

dta3_sig = zeros(1,symlen*mulrate);
dta3_sig(1:mulrate:end) = dta2_symbols;

#figure(); plot (dta3_sig, "r+");

##fir send
[fir_rcos]=rcosfir(0.25,[-3,3],mulrate,1,'sqrt');

dta4_baseband = conv(dta3_sig,fir_rcos,'same');

#plot (dta4_baseband(1:mulrate:end), "g*");
#figure; plot(fir_rcos);
##Trans

# to rx
rf_sym_rate = 1000;
rf_sample_rate = rf_sym_rate * mulrate;



dta5_recv = awgn (dta4_baseband, 12);

figure();plot (dta5_recv(1:mulrate:end), "r.");

##fir recv
dta6_filted = dta5_recv;
dta6_filted = conv(dta5_recv,fir_rcos,'same');

figure();plot (dta6_filted(1:mulrate:end), "b.");

dta7_sampled = dta6_filted([1:mulrate:end]);
#figure();plot (dta7_sampled, "b.");

#dta8_est = qamdemod (dta7_sampled, 4);
dta8_est = pskdemod (dta7_sampled, 2,0,"gray");

biterr (dta1_bits, dta8_est)

#figure();plot (real(dta4_baseband),'r');
#figure();plot (real(dta6_filted),'b');

2 窗口统计去直流分量

有些时候，收到的向量具有一个整体的直流分量，导致其不再围绕原点分布。表现在复平面上，就是一坨位置跑到别处去。这样导致基于原点进行角度测量的三角函数都没有办法使用了。

解决此问题的方法很简单，就是统计一个窗口里的坐标的均值，并搬移到原点去。上文代码：

//2. 窗口统计去直流分量
sum_win[0] -= stati_win[clk%WINSZ][0];
sum_win[1] -= stati_win[clk%WINSZ][1];
sum_win[0] += fval_i;
sum_win[1] += fval_q;
stati_win[clk%WINSZ][0] = fval_i;
stati_win[clk%WINSZ][1] = fval_q;
const double dcremoved[2] {fval_i - sum_win[0]/WINSZ, fval_q - sum_win[1]/WINSZ };

就干了这个事情。等一等，为什么没有for循环？这里面又使用了第二个环状统计缓存器，即均值统计环状缓存。

缓存记住最新的WINSZ = 4000个坐标，以及他们的和sum_win。
新的数据到来，sum_win 先减去最老的那个时刻的值，并加上新时刻的值。
如此循环，每个时钟下，窗口都能跟踪当前的均值了。

3 时钟和频率同步

这是最关键的部分，首先是时钟同步，而后是频率同步。

时钟同步是为了获得地鼠盘，让地鼠稳定的出现在一个看不见的圆圈上，而不是乱窜。

频率同步就是打地鼠，用一个角度跟踪器（软件实现）或者锁相环（硬件）跟踪残差频率造成的相位移动。

3.1 在恰当的时刻获取符号

在4倍采样率下，由于不知道下图红色的正确位置在哪里，所以随便抽取一路作为x,y的坐标值是不行的。

recv

如何获取正确的位置呢？我们通过观察，这些正确位置上，矢量均远离坐标原点；在过渡位置上，一半以上的点贴近坐标原点。因此，只要统计当前四个偏移位置（01,2,3）上，4000个样点的矢量长度和，和最大的哪个就是最佳位置。

//3. 最佳采样位置跟踪
const int curr_offv = clk % 4;
clk_offset[curr_offv] += (dcremoved[0]*dcremoved[0] + dcremoved[1] * dcremoved[1]); //符号时钟位置同步

这里求矢量长度没有取SQRT，为了省计算。其实是一样的，只是比大小，sqrt不改变其单调性。

由于收发双方的时钟存在误差，这个最佳位置是会不断移动的。一小会是2，后面可能就成了3,0,1，或者反方向编程了1,0,3,2的重复。所以，每隔一段时间，我们要重新评估这个最佳位置，并只在最佳位置上抽取。其逻辑片段：

static unsigned long long clk = 0, last_synclk = 0;
static int bestOff = 0;
//逐个点步进
for (int i=0;i<splen;++i)
{
//...
//3. 最佳采样位置跟踪
const int curr_offv = clk % 4;
clk_offset[curr_offv] += (dcremoved[0]*dcremoved[0] + dcremoved[1] * dcremoved[1]); //符号时钟位置同步
//在最佳位置输出
if (curr_offv == bestOff)
{
//...
//解调后的01比特
dp_bitbuf.push_back( rp[0] < 0? 0: 1 );
}
//错开最佳点2符号进行重新评估
if (last_synclk + WINSZ < clk && ((clk+2) % 4)==bestOff)
{
last_synclk = clk;
int maxo = 0;
double maxv = clk_offset[0];
if (clk_offset[1] > maxv) { maxo = 1; maxv = clk_offset[1];}
if (clk_offset[2] > maxv) { maxo = 2; maxv = clk_offset[2];}
if (clk_offset[3] > maxv) { maxo = 3; maxv = clk_offset[3];}
bestOff = maxo;
clk_offset[0] = 0;clk_offset[1] = 0;
clk_offset[2] = 0;clk_offset[3] = 0;
}
++clk;
}

错开最佳点2符号进行重新评估，是为了稳定、隐含的解决双方钟差不同步需要进行符号填补、扣除的操作。比如收方每收10000个符号，发方发了10017个符号，那就要悄默默的踢出17个，否则就乱套了。这种踢出行为，就是在 bestOff调整时顺带完成的。bestOff变了，导致下一次输出 if (curr_offv == bestOff) 判断会提前、退后一个点。为了这个行为的稳定，对bestOff的调整要避开当前最佳点，越远越好，于是时机选择在 ((clk+2) % 4)==bestOff。

3.2 测量并咬住相位

一旦找到了正确的时钟位置，测量相位就是一个 x,y坐标到角度的变化了：

static unsigned long long clk = 0, last_synclk = 0;
static int bestOff = 0;
static double curr_dp = 0;
double phy = 0;//锁相环误差
if (curr_offv == bestOff)
{
//锁相旋转
double rt[2]{cos(-curr_dp),sin(-curr_dp)};
const double out[2]{cache_win[(clk+4)%WINSZ][0],cache_win[(clk+4)%WINSZ][1]};
double rp[2]{
out[0] * rt[0] - out[1] * rt[1],
out[0] * rt[1] + out[1] * rt[0]
};
//失败重置
//...
//更新环路
curr_dp += (phy/2);
curr_dp =wrapto2pi(curr_dp );
//解调后的01比特
dp_bitbuf.push_back( rp[0] < 0? 0: 1 );
}
//...
++clk;
}

当然，如果角度误差巨大，说明跟踪失败了，可以重置：

//失锁重置，即重新测量相位误差
phy = atan_r(rp[1],rp[0]);
if (phy >= c_pi/4 || phy <=-c_pi/4)
{
curr_dp = atan_r(out[1],out[0]);
rt[0] = cos(-curr_dp);
rt[1] = -sin(curr_dp);
rp[0] = out[0] * rt[0] - out[1] * rt[1];
rp[1] = out[0] * rt[1] + out[1] * rt[0];
phy = atan_r(rp[1],rp[0]);
++bad_angle;
}

4. 最终效果

通过上述操作，最终紧紧咬住了BPSK 180度的相位变化，获得了正确的数据流。由于不知道确切的相位是0还是180，可能存在极性颠倒。如何抗颠倒，交给上层协议去做了。

完整的SDR实现了双工的协议栈，用主对方两个频率实现全通的IP网络连接。对于从0开始实现的纯C/C++ SDR大玩具，可以非常细致的体会真正的通信系统设计实现环节的各种坑。目前还没有涉及到精确定时。精确定时在粗大的颗粒度下，SDR是可以来做的。要在20ms以下进行定时、TDMA操作，恐怕需要再踩一些坑。不过能够用有限的知识，控制低成本的实验设备完成全套流程，可玩性已经非常高了。

SDR
完整代码参考前文的Git仓库。发行版参考前文连接。

5.思考体会

通过这个实验，我们发现对于基带信号，直接从复平面的特性去思考，要比从受限于模拟器件的角度得到的原理图去思考更直接。使用通用计算机进行操作，或许有更为简便的算法等待开发。应该有教材在介绍传统的解调思路前，把这些思考说清楚，这样学生在学习时，就更为有针对性了。

原文地址：https://blog.csdn.net/goldenhawking/article/details/136462440

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

【大数据学习 | kafka高级部分】kafka的快速读写
机械磁盘的文件检索需要使用到磁头进行不断扫描数据，如果存储大量的小文件或者存储位置不同的时候需要不停的扫描检索文件的位置，这个过程是非常浪费时间的，但是kafka的数据完全以追加的方式存储到磁盘中的，
阅读更多2024-11-07
i2c-tools 4.3 for Android 9.0
Android 9.0下编译i2c-tools 4.3
阅读更多2024-11-07
MySQL基础篇总结
数据定义语言，用来定义数据库对象（数据库、表、字段）。数据控制语言，用来创建数据库用户、控制数据库的控制权限。数据库操作查询所有数据库：查询当前数据库：创建数据库：CREATE DATABASE [
阅读更多2024-11-07
10DSP学习-利用syscfg配置ADC，并使用EPWM触发转换
介绍了如何使用syscfg配置F28379D的ADC采样
阅读更多2024-11-07
基于python多准则决策分析的汽车推荐算法设计与实现
随着汽车市场的快速发展和消费者需求的多样化，汽车选择变得愈加复杂。为了帮助消费者在众多汽车选项中做出明智的决策，基于多准则决策分析（MCDA）的汽车推荐算法应运而生。本研究旨在设计和实现一种基于 Py
阅读更多2024-11-07
python语言基础-4 常用模块-4.4 random模块
声明：本内容非盈利性质，也不支持任何组织或个人将其用作盈利用途。本内容来源于参考书或网站，会尽量附上原文链接，并鼓励大家看原文。侵删。
阅读更多2024-11-07
深入解析Vue3：从入门到实战（详细版）
要从容地着手做一件事，但一旦开始，就要坚持到底
阅读更多2024-11-07
Java15
**String类**：提供了丰富的方法来处理字符串，如`compareTo`、`contains`、`equals`、`getBytes`、`indexOf`、`replace`、`split`、`
阅读更多2024-11-07
8.qml中tableview使用QtQuick.Controls2
qquicklistmodel与qquickfolderlistmodel都是派生于qabstractlistmodel。tableview.model 与 delegate中的model.index
阅读更多2024-11-07
C++入门
定义命名空间，需要使用到namespace关键字，后面跟命名空间的名字，然后接⼀对{}即可，{}中即为命名空间的成员。命名空间中可以定义变量/函数/类型等。• namespace本质是定义出⼀个域，这
阅读更多2024-11-07