图形几何之美系列:法向量计算之轮廓有向面积辅助法
“ 垂直于平面的直线所表示的向量为该平面的法向量,可以通过法向量识别平面正反面。法向量是轮廓或面的重要特征,求轮廓法向是一种基础的几何工具算法,在图形几何、图像处理等领域具有广泛的应用。”
法向量是轮廓或面的基础几何特征,在实际工程中存在广泛的应用。在计算机视觉领域,法向量可以用于检测图像中的边缘和角点。在三维建模和渲染中,法向量可以帮助计算光线与曲面的相交,从而实现阴影效果和渲染,使图像更加真实。在立体几何中,法向量可用于求解点到平面的距离、异面直线间的距离、直线与平面所成的角、二面角的大小等问题。
1.前言
有多种方法可计算轮廓的法向量,如根据轮廓类型进行法向量的计算、轮廓有向面积辅助法、Newell向量法等。
如上文多边形轮廓面积计算中的内容所述,轮廓的法向量和面积密切相关,我们常说的法向量为单位法向量,而模长等于面积的法向量是多边形轮廓多维度的几何和物理属性,更能表达轮廓的几何特征。
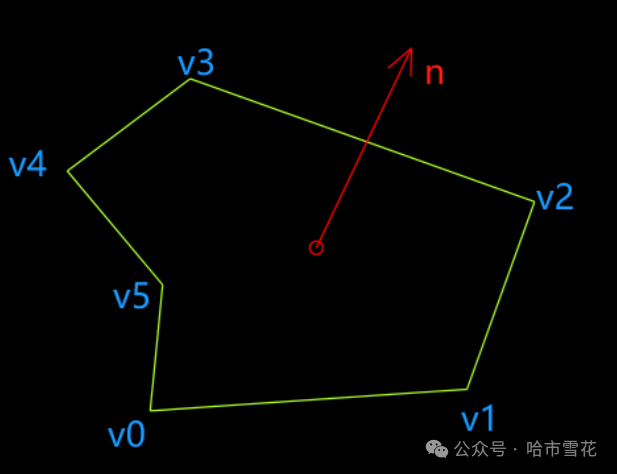
需要注意的是由于浮点数存储和运算的精度损失,可能造成求轮廓法向的精度损失,如角点由于精度损失并非精确的在一个平面上(而是在容差范围内属于一个平面)、角点距离很近导致可能进一步影响法向计算的精度等。
2.根据轮廓类型计算法向量
2.1.三角形法向量
可以通过相邻边方向叉乘得到三角形法向量,边的选择将决定得到的法向量是正向还是反向,当我们选择边与其后续邻接边进行叉乘时,得到的就是三角形正向的法向量。
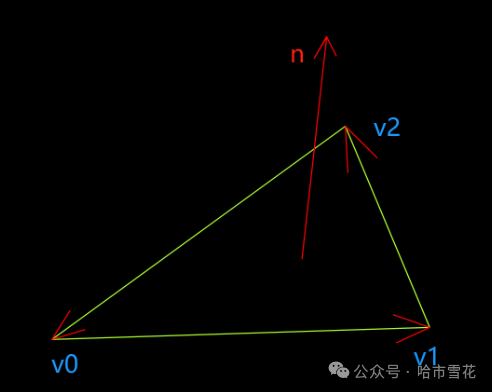
2.2.凸多边形法向量
三角形是凸多边形的类型之一,凸多边形的法向量计算同样可以用选择边与其后续邻接边进行叉乘得到。
需要注意的是由于浮点型存储和计算精度损失等原因,凸多边形上的点可能存在略微偏离所在平面,这时候参与运算的边如果恰好有非常短的边时,由其构造的相量与所在平面夹角将不为0,甚至偏离较大,这将导致求得的法向量存在较大的误差。
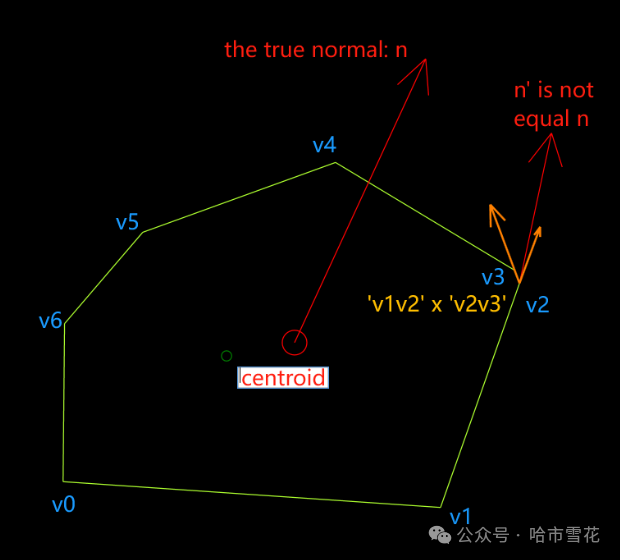
一种较好的办法是考虑所有边,即所有边参与运算,这将较大程度的对局部精度损失引起的误差进行“纠偏”。
提示
后续章节将涉及如何使法向量计算保持较高的精度。
3.任意多边形法向量
3.1.有向面积辅助法
在实际工程场景中,往往需要考虑任意多边形的情况,如实体参与布尔运算后存在不规则形状的面,需要计算面的法向量以正确的进行效果显示。
当多边形含有凹角时,运用上述“选择边与其后续邻接边进行叉乘”得到的法向量会是反向的,这时候我们不知道哪个是凹角,因为法向量还没有被正确的计算出来。这就需要一种通用的法向量计算方法。
补充
任意多边形法向量计算方案不止一种,如前文所述,本文将针对“轮廓有向面积辅助法”进行讲述,有关其他方法可联系作者或继续关注公众号文章。
从轮廓“正面”看向轮廓,轮廓是逆时针的,从轮廓“反面”看向轮廓,轮廓是顺时针的,轮廓的顺逆时针只是相对的,取决于怎么看向轮廓。
当轮廓法向朝向我们时,轮廓是逆时针的,这时轮廓有向面积为正,也就是从正面看,轮廓有向面积是正的。你可能大概有思路了,我们继续分析,
补充
基于轮廓正向法向量时,轮廓有向面积为正;基于轮廓反向法向量时,其面积为负。
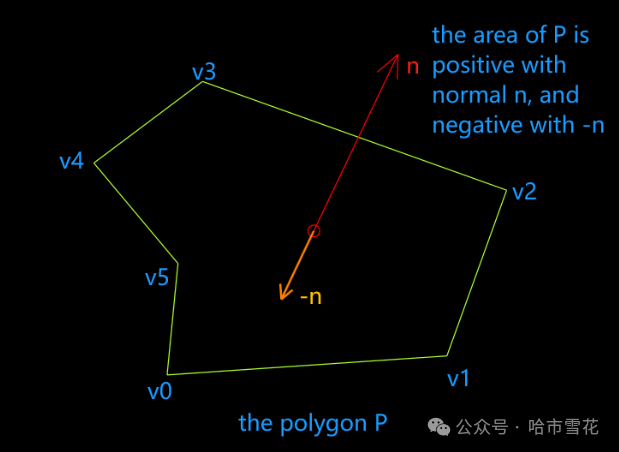
在不考虑正负的情况下,我们比较容易求得轮廓的法向量(可以运用“选择边与其后续邻接边进行叉乘”),然后基于此法向量进行轮廓面积计算,如果为正,则该法向量为正向法向量,如果面积为负,则该法向量为反向法向量,对其取反即得正向法向量。
提示
轮廓面积计算有多种方法,可以通过微积分方法或衍生的梯形投影和等方法,或采用Newell方法,详细可参考作者相关文章。
3.2.精度的提高
上文提到,由于浮点型存储和计算精度损失等原因,凸多边形上的点可能存在略微偏离所在平面,这时候参与运算的边如果恰好有非常短的边时,由其构造的相量与所在平面夹角将不为0,甚至偏离较大,这将导致求得的法向量存在较大的误差。
一种提高精度的思路是考虑所有相邻边得到的法向因素,进行加权平均,权重值为相邻边的夹角angle因素(弧度表示法),夹角在[0,PI/2)时取原值,在[PI/2,PI]时取PI-angle,因为在相同的条件下上述取值越大计算的精度越高,其对法向的贡献度越大,即权重值越大。
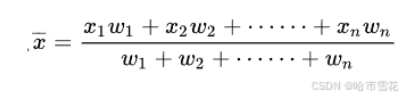
图:加权平均思想
提示
试想一下,当两条边无限接近于共线的情况,那么由它们计算得到的法向量无限接近于(0,0,0)。
仍然需要考虑凹凸角情况,统一将凹角或凸角计算得到的法向进行取反即可,因为符号会通过计算面积得到。一种实践是判断当前计算的法向是否与已计算过的法向存在夹角大于接近于PI值的情况(如PI/6*5,即150°),如果存在即取反,这样所有的法向被统一在面的一个方向了。
4.总结
对于特定规则的多边形,如三角形、凸多边形,计算法向量较为简单,可以运用“选择边与其后续邻接边进行叉乘”,但需要关注精度话题。
多边形有向面积与其法向量密切相关,对于任意多边形的法向量计算可以采用Newell法进行计算,公式简洁清晰,计算量较小,同时可保持较高的精度。
当然也可参考轮廓有向面积辅助法进行计算,同样可保持较高的精度,但其计算量相对Newell法较大。
欢迎关注,图形几何之美系列 将继续更新......
原文地址:https://blog.csdn.net/baidu_38621657/article/details/143804279
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
