有序logistic回归分析模型原理与案例教程
有序Logistic回归和多分类Logistic回归的因变量均有多个分类水平,但是前者分类水平是有顺序、等级属性的。比如临床试验的疗效分为无效、好转、有效和治愈四个等级,在社会调查类研究满意度分为1~5层级。
1. 模型原理
由于因变量是等级资料的特征,有序Logistic回归模型称之为累加Logit模型,其原理是对因变量水平分割后形成多个二元Logistic回归模型,同时假设多个模型中的自变量回归系数不变,不同的仅是模型的常数项,可通俗理解为模型的回归曲线是平行的。
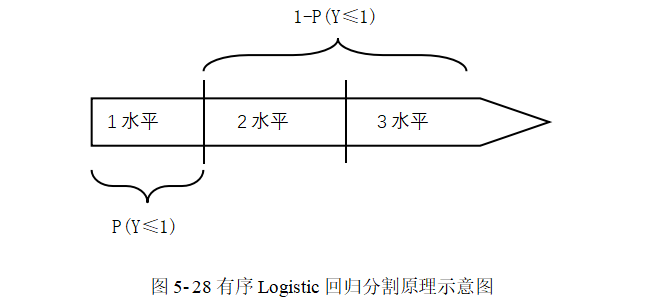
如图 5-28所示,以Y有3个水平为例,编码依次为1、2、3,按序依次产生两个分割点,拆分出两个二元Logistic回归模型。第一个模型为(1 vs 2+3),第二个模型为(1+2 vs 3),一般上参照水平均取较高等级。也就是说,k个水平将得到k-1个二元Logistic回归模型。这k-1个模型要求回归自变量不变,仅常数项改变。
2. 重要概念
(1) 连接函数
连接函数可以理解为是累计概率的转换形式,用于累计概率模型的估计。有序Logistic回归通常包括五种连接函数,具体见下表 5-31。
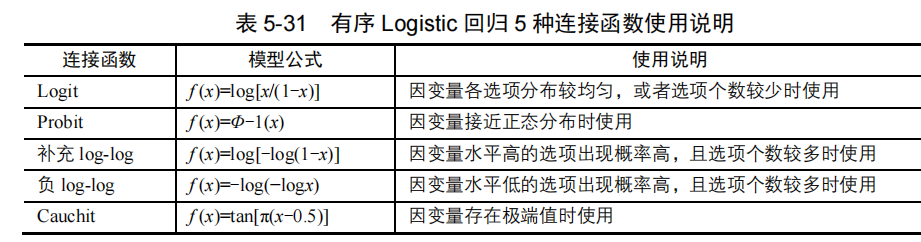
平台默认使用Logit连接函数,如模型没有特殊要求,一般建议使用Logit连接函数,其在因变量分类水平较少时较为常用。连接函数可能会影响到对平行性检验,如果平行性检验无法通过时,可考虑根据因变量分布情况选择更为合适的连接函数。
(2) 平行性检验
累加Logit模型需要对因变量分类水平进行分割,然后对分割后的数据进行Logistic回归,此时要求分割后的模型参数满足平行性,即Logistic回归模型中的各自变量偏回归系数要求相等。
该检验假设数据满足平行性,因此只需要看检验的p值是否大于0.05,若p值大于0.05则说明平行,反之如果p值小于0.05则不满足平行性条件。如果不满足,可以结合有序结局的比例分布情况选择合适的连接函数,重新进行分析和检验。如最终认定无法满足该条件,则可考虑使用多分类logistic回归进行分析。
3. 有序Logistic回归分析步骤
有序Logistic回归分析的步骤和前面的二元、多分类Logistic回归略有不同,如下图 5-29所示。
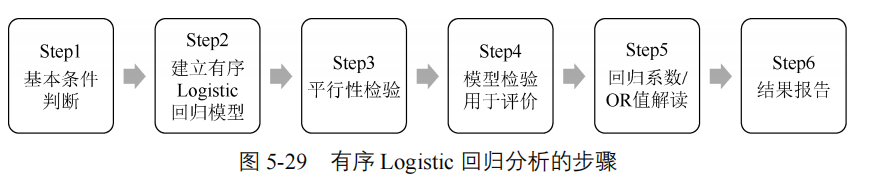
(1) 基本条件判断
因变量须是等级数据,例如药物治疗的疗效(无效、有效、显著有效),或者顾客满意度(非常不满意、不满意、一般、满意、非常满意)。共线性、异常值等要求同前面二元Logistic回归。
(2) 建立Logistic回归模型
一般选因变量的最大水平作为参考水平,先以Logit连接函数建立有序Logistic回归模型。也可以根据专业经验调整因变量的编码水平,方便后面结果的解释分析。
(3) 平行性检验
模型分割后要求各自变量偏回归系数要求相等,需要通过平行性检验。如果不满足平行性条件,则可考虑调整连接函数重新进行检验,如最终结果认定无法满足,则考虑将有序因变量视为无序多分类类型,使用多分类logistic回归进行分析。
步骤(4) (5) (6)的分析和前面二元、多分类Logistic回归基本一致,此处不做赘述。
4. 有序Logistic回归实例分析
【例5-10】研究性别和两种治疗方法对某病疗效的影响,疗效的评价分为三个等级,无效、有效和显效,数据变量赋值见表 5-32。试分析疗效与性别、疗法之间的关系。案例数据来源于张文彤(2002),数据文档见“例5-10.xls”。
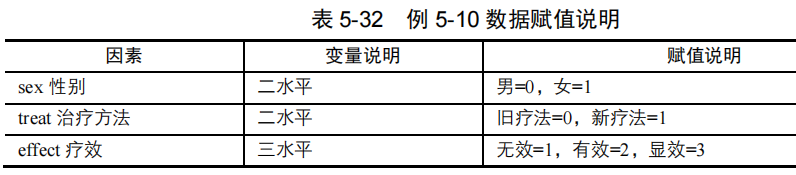
1) 基础条件判断
治疗效果分为三个层级,依次是无效=1,有效=2,显效=3,为有序的多分类变量。主要考虑性别和新旧两种治疗方法对疗效的影响,应采用有序Logistic回归。
2) 建立有序Logistic回归模型
数据读入平台后,仪表盘中依次选择【进阶方法】→【有序Logit】模块,将“疗效”拖拽至【Y(定类)】,“性别”和“疗法”变量拖拽至【X(定量/定类)】。
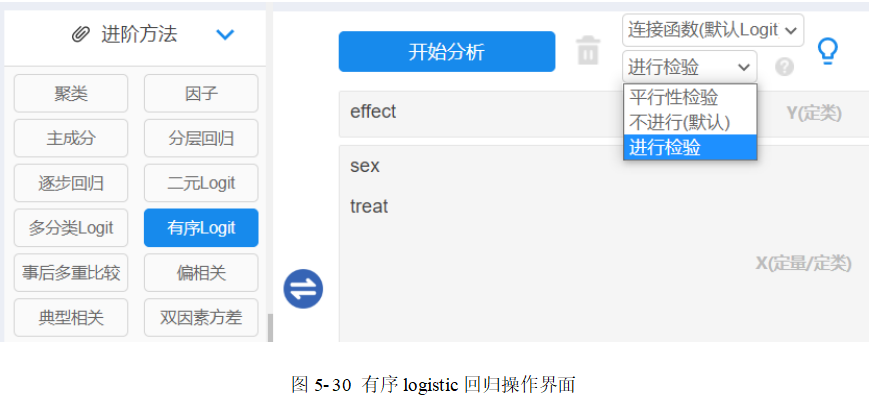
在【平行性检验】下拉框内选择【进行检验】,在【连接函数】下拉框内默认勾选【默认Logit】,相关操作见图 5-30。
3) 平行性检验
作为有序logistic回归的适用条件,我们先判断数据是否满足平行线条件,本例结果见表5-33。

经检验,卡方值=1.649,p=0.48﹥0.05,模型通过平行性检验,使用有序Logistic回归进行分析是合适的。
4) 模型显著性检验

如表5-34所示,经检验,卡方值=19.887,p﹤0.01,认为模型总体上有统计学意义,模型有效。反之如果p值大于0.05则提示模型无效。
表中的AIC、BIC,以及-2LL,和二元Logistic回归解读一致,均为取值越小越好,主要用于多个模型间的比较,此处意义不大。
5) 模型回归系数、OR值
本例因变量有3个等级,将得到2个模型,这两个模型中自变量的偏回归系数不变而常数项不同,结果如下表535所示。
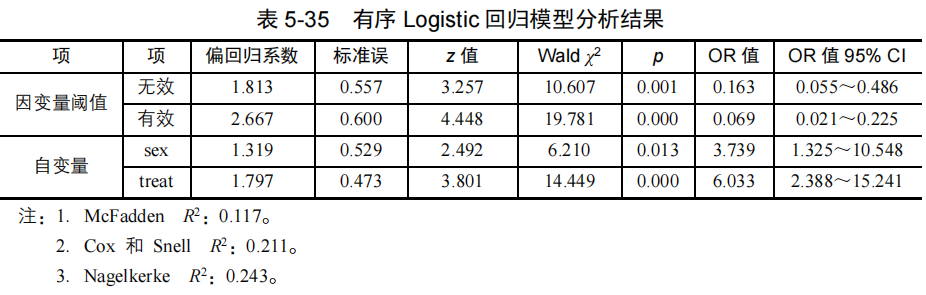
表中“因变量阈值”指的是两个模型常数项估计结果,“自变量”则是两个模型的自变量偏回归系数的估计结果。
两个模型的常数项依次为1.813、2.667,经Wald 卡方值检验,性别“sex”(Wald 卡方=6.210,p=0.013﹤0.05),疗法“treat”(Wald 卡方=14.449,p﹤0.01),认为性别和疗法对疗效的作用都有统计学意义。性别“sex”和疗法“treat”的OR值为依次为3.739、6.033,表明对女性患者来说疗效优于男性,而新疗法的疗效优于旧疗法。
6) 结果报告
根据表中常数项和偏回归系数(注意,写表达式时回归系数取负数),可以写出两个模型的表达式为:
logit[P(effect≤无效)/(1-P(effect≤无效))]=1.813-1.319×sex-1.797×treat
logit[P(effect≤有效)/(1-P(effect≤有效))]=2.667-1.319×sex-1.797×treat
性别和疗法对疗效的作用有显著影响,对女性患者来说疗效优于男性,而新疗法的疗效优于旧疗法。
以上内容摘自《SPSSAU科研数据分析方法与应用》第5章——相关影响关系研究,书中不仅涵盖了数据清理、统计分析和模型构建等内容,还提供了丰富的案例,以便于读者在实际研究中应用。

原文地址:https://blog.csdn.net/m0_37228052/article/details/143576567
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
