图论系列(dfs)9/24
岛屿问题:
二叉树dfs遍历的框架代码:
要有一个终止条件、访问相邻节点;
public void dfs(Treenode root){
if(root==null)return;
dfs(root.left);
dfs(root.right);
}网格dfs遍历的框架代码:
public void dfs(int[][] grid,int x,int y){
//如果x、y坐标不在网格里面 直接return;
if(!inArea(grid,x,y)){
return;
}
//递归遍历四个结点
dfs(grid,x-1,y);
dfs(grid,x+1,y);
dfs(grid,x,y-1);
dfs(grid,x,y+1);
}
public boolean inArea(int[][] grid,int x,int y){
if((x<0||x>=grid.length)&&(y<0||y>=grid[0].length))return false;
return true;
}二叉树中不会遇到重复的结点;但是在网格中可能遇到重复的节点;
直接将grid的值改为2;
void dfs(int[][] grid, int r, int c) {
// 判断 base case
if (!inArea(grid, r, c)) {
return;
}
// 如果这个格子不是岛屿,直接返回
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}一、岛屿数量
示例 1:
给定一个二维矩阵数组,1代表陆地;0代表海洋。陆地连起来的地方叫岛屿;求岛屿的数量
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
左上角一片陆地是连着的。因此只有一块岛屿。
思路:
跟求连通块是一样的道理。
代码:
class Solution {
public int numIslands(char[][] grid) {
int count=0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]-'1'==0)count+=dfs(grid,i,j);
}
}
return count;
}
public int dfs(char[][] grid,int x,int y){
if(!inArea(grid,x,y)||grid[x][y]!='1')return 0;
grid[x][y]='2';//将该点标记为已经访问过的
dfs(grid,x+1,y);
dfs(grid,x-1,y);
dfs(grid,x,y+1);
dfs(grid,x,y-1);
return 1;
}
public boolean inArea(char[][] grid,int x,int y){
if((x<0||x>=grid.length)||(y<0||y>=grid[0].length))return false;
return true;
}
}二、岛屿的最大面积
题意和上题一样
思路:
在上一道题的基础上,不仅要求岛屿的数量,还要求每一块岛屿的面积。
代码:
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int max=0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]==1)max=Math.max(max,dfs(grid,i,j));
}
}
return max;
}
public int dfs(int[][] grid,int x,int y){
if(!inArea(grid,x,y)||grid[x][y]!=1){
return 0;
}
grid[x][y]=2;
return 1+dfs(grid,x+1,y)+dfs(grid,x-1,y)+dfs(grid,x,y+1)+dfs(grid,x,y-1);
}
public boolean inArea(int[][] grid,int x,int y){
if((x>=grid.length||x<0)||(y>=grid[0].length||y<0))return false;
return true;
}
}三、岛屿的周长
题意和上面类似,只是让求岛屿的周长。
示例 1:
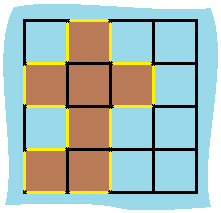
输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] 输出:16 解释:它的周长是上面图片中的 16 个黄色的边
思路:
仔细观察,岛屿的周长都是陆地的边和海洋以及边界处的相交;
因此当我们向左遍历遇到的是边界,那么周长++;如果遇到的是海洋,周长++;
if(!inArea(grid,x,y)||grid[x][y]==0){
return 1;
}如果不是交界也不是陆地;那么直接返回0;
if(grid[x][y]!=1)return 0;代码:
class Solution {
public int islandPerimeter(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
return dfs(grid, i, j);
}
}
}
return 0;
}
public int dfs(int[][] grid,int x,int y){
if(!inArea(grid,x,y)||grid[x][y]==0){
return 1;
}
if(grid[x][y]!=1)return 0;
grid[x][y]=2;
return dfs(grid,x-1,y)+dfs(grid,x+1,y)+dfs(grid,x,y-1)+dfs(grid,x,y+1);
}
public boolean inArea(int[][] grid, int x, int y) {
if ((x < 0 || x >= grid.length) || (y < 0 || y >= grid[0].length))
return false;
return true;
}
}原文地址:https://blog.csdn.net/2301_78191305/article/details/142486292
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
