【微积分】三角函数求导积分公式的巧妙记忆
三角函数积分求导公式的巧妙记忆
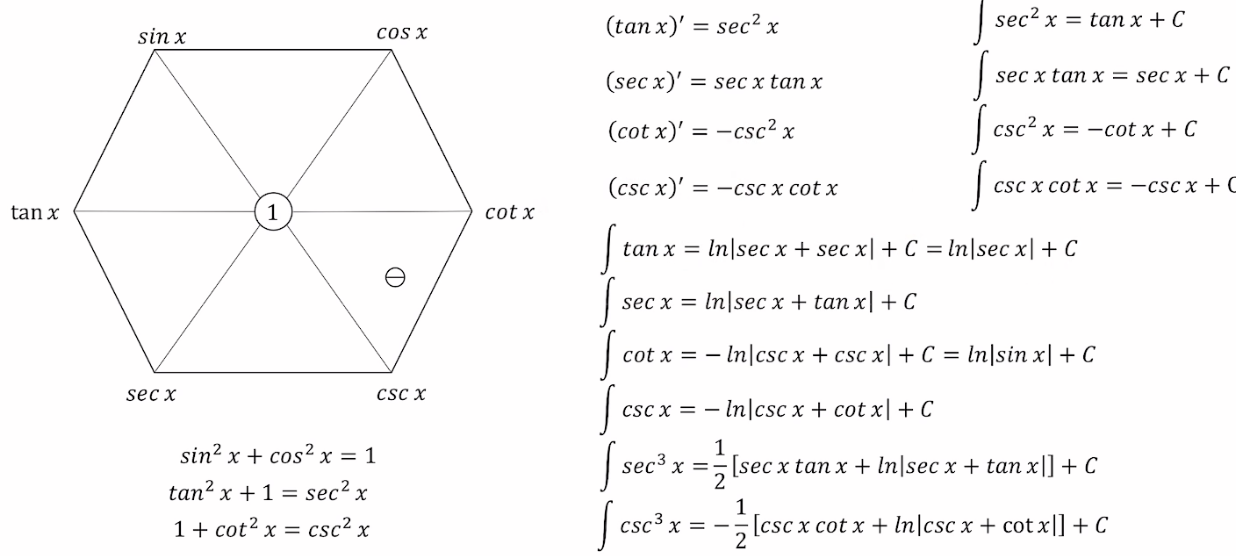
图像的整体记忆:
上面是sinx cosx
下面也是s开头,secx,cscx
中间是tanx cotx
解释说明:
1️⃣ 对角线互为倒数,即sinx对角线是cscx,这样我们可以更好记住这个六边形图像。
2️⃣顺时针方向上,某一个三角函数=接下来的两个三角函数之比,如tanx=sinx/cosx
3️⃣平方和规律,大六边形由6个小三角形组成,其中的三个倒三角形的上两个顶点平方和,等于下面那个点的平方
4️⃣ 对三角函数无论是积分还是求导,我们发现规律都是两个三角函数组合的形式。
中下下,如果是中间的tanx,cotx,他的导数就是,他下面那个三角函数乘于两次,注意那个带负号的三角函数分区,他求导和积分要带负号。
下下中,同理
导相乘,对对和:求导是相乘,积分是加一起。
5️⃣ 记住导数,积分导数互为逆运算,所以不难记住。
6️⃣三次方公式也要记忆,二分之一导+和别忘了csc有负号
重要的说明:
ln ∣ sec x + s e c x ∣ + C = ln ∣ 2 sec x ∣ + C = ln 2 + ln ∣ sec x ∣ = ln ∣ sec x ∣ + C 负号 − ln ∣ csc x + csc x ∣ + C = − ln ∣ 2 csc x ∣ + C = − ln 2 + − ln ∣ csc x ∣ = − ln ∣ csc x ∣ + C = ln ∣ s i n x ∣ + C 负号提进去 − ln ∣ csc x + cot x ∣ + C = 可以把负号提进去,取倒数整理 = 书上公式 = ln ∣ csc x − cot x ∣ 这个记哪个都行 \ln \left|\sec x + secx\right| + C = \ln \left|2\sec x\right| + C = \ln 2+ \ln \left|\sec x\right|= \ln \left|\sec x\right| + C负号\\\: - \ln \left|\csc x + \csc x\right| + C = - \ln \left|2\csc x\right| + C = - \ln 2 + - \ln \left|\csc x\right| = - \ln \left|\csc x\right| + C = \ln \left|sinx\right| + C负号提进去\\\: - \ln \left|\csc x + \cot x\right| + C = 可以把负号提进去,取倒数整理 = 书上公式 = \ln \left|\csc x - \cot x\right|这个记哪个都行\:\: ln∣secx+secx∣+C=ln∣2secx∣+C=ln2+ln∣secx∣=ln∣secx∣+C负号−ln∣cscx+cscx∣+C=−ln∣2cscx∣+C=−ln2+−ln∣cscx∣=−ln∣cscx∣+C=ln∣sinx∣+C负号提进去−ln∣cscx+cotx∣+C=可以把负号提进去,取倒数整理=书上公式=ln∣cscx−cotx∣这个记哪个都行
原文地址:https://blog.csdn.net/weixin_62613321/article/details/138818373
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
