12种常见的华为杯数学建模竞赛matlab代码(建议收藏)
1.使用神经网络模型(向量量子化方法LVQ)解决分类/预测问题
clc;clear;% 第一类蝗虫的触角和翅膀p1 = [1.24, 1.27; 1.36, 1.74; 1.38, 1.64;1.38, 1.82; 1.38, 1.90; 1.40, 1.70;1.48, 1.82; 1.54, 1.82; 1.56, 2.08];% 第二类蝗虫的触角和翅膀p2 = [1.14, 1.82; 1.18, 1.96; 1.20, 1.86;1.26, 2.00; 1.28, 2.00; 1.30, 1.96];% 合并两个类的数据p = [p1; p2]';% 分别获取触角和翅膀的最小值与最大值pr = minmax(p);% 目标分类:第一类蝗虫是 [1; 0],第二类蝗虫是 [0; 1]goal = [ones(1, 9), zeros(1, 6); zeros(1, 9), ones(1, 6)];% 可视化两类数据plot(p1(:, 1), p1(:, 2), 'h', p2(:, 1), p2(:, 2), 'o');% 创建 LVQ 神经网络,4个隐层神经元,分类比例 [0.6, 0.4]net = newlvq(pr, 4, [0.6, 0.4]);% 训练神经网络net = train(net, p, goal);% 使用训练好的网络进行分类Y = sim(net, p);% 待分类数据x = [1.24, 1.80; 1.28, 1.84; 1.40, 2.04]';sim(net, x)
2.使用神经网络模型(向后传播算法BP)解决蝗虫分类问题
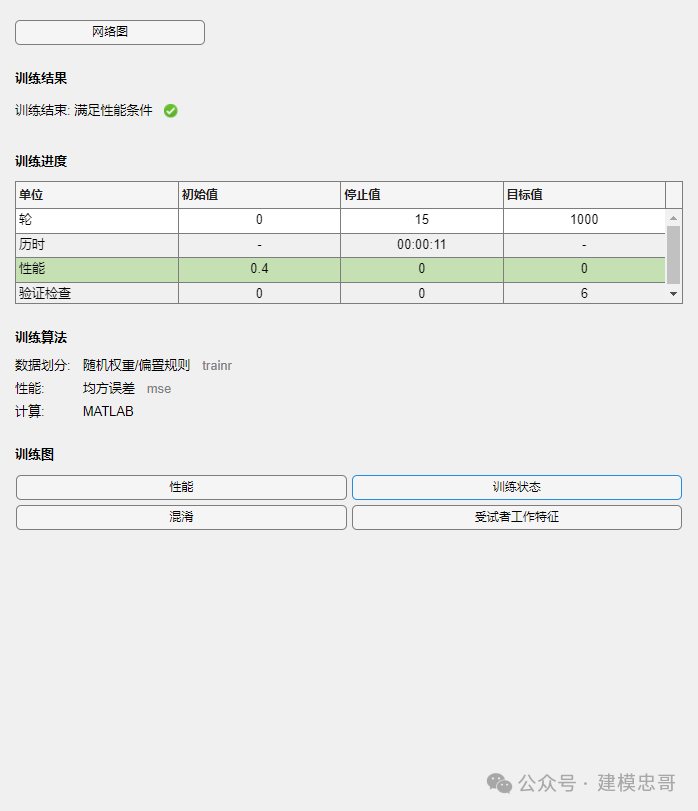
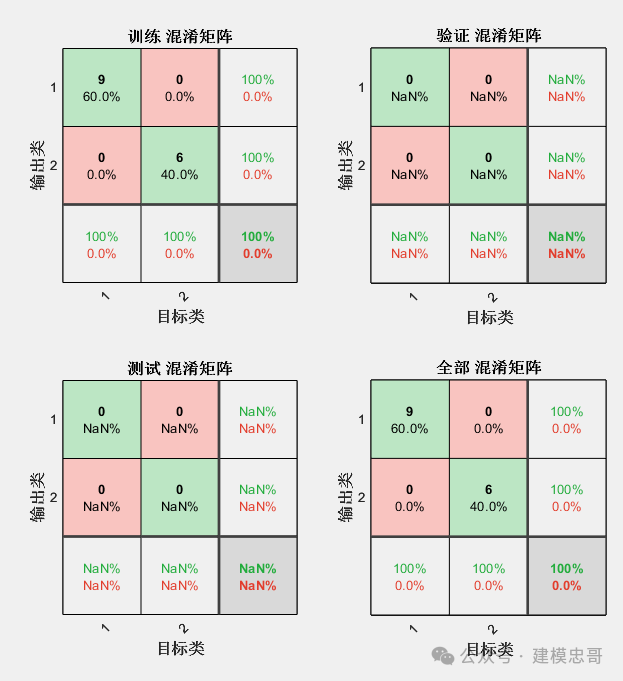
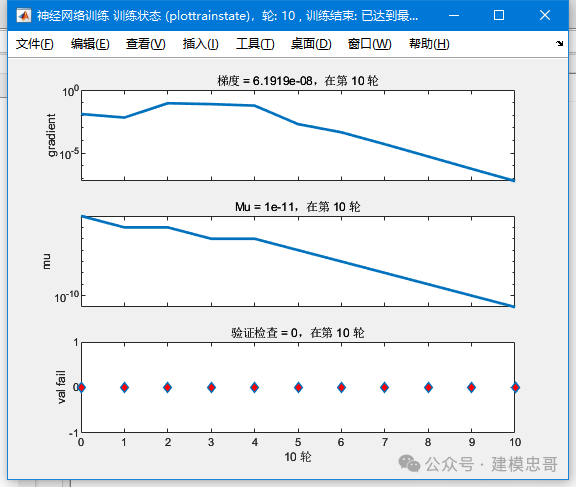
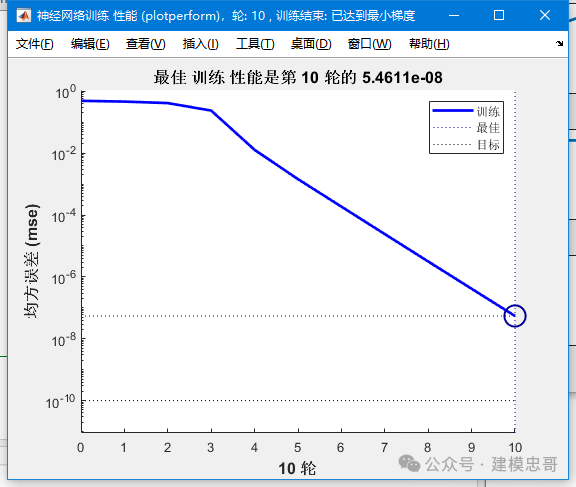
%%clc, clear% 第一类蝗虫的触角和翅膀p1 = [1.24, 1.27; 1.36, 1.74; 1.38, 1.64;1.38, 1.82; 1.38, 1.90; 1.40, 1.70;1.48, 1.82; 1.54, 1.82; 1.56, 2.08];% 第二类蝗虫的触角和翅膀p2 = [1.14, 1.82; 1.18, 1.96; 1.20, 1.86;1.26, 2.00; 1.28, 2.00; 1.30, 1.96];p = [p1; p2]';% 分别获取触角和翅膀的最小值与最大值pr = minmax(p);goal = [ones(1, 9), zeros(1, 6); zeros(1, 9), ones(1, 6)];plot(p1(:, 1), p1(:, 2), 'h', p2(:, 1), p2(:, 2), 'o');net = newff(pr, [3, 2], {'logsig', 'logsig'}); %函数newff建立一个可训练的前馈网络%----参数介绍-----%% net=newff(PR,[S1 S2 ...SN],{TF1 TF2...TFN},BTF,BLF,PF)% PR:Rx2的矩阵以定义R个输入向量的最小值和最大值;% Si:第i层神经元个数;% TFi:第i层的传递函数,默认函数为tansig函数;% BTF:训练函数,默认函数为trainlm函数;% BLF:权值/阈值学习函数,默认函数为learngdm函数;% PF:性能函数,默认函数为mse函数。net.trainParam.show = 10; % 现实频率,这里设置为没训练20次显示一次net.trainParam.lr = 0.05; % 学习速率,这里设置为0.05net.trainParam.goal = 1e-10; % 训练目标最小误差net.trainParam.epochs = 50000; % 训练次数,这里设置为300次net = train(net, p, goal);% 待分类数据x = [1.24, 1.80; 1.28, 1.84; 1.40, 2.04]';% 分类:调用Simulink。输出的是什么信息?y0 = sim(net, p);y = sim(net, x);
代码主要通过前馈神经网络来对蝗虫的触角和翅膀数据进行二分类,训练后神经网络能够对新的蝗虫数据进行分类。
3.BP神经网络语音识别
%% 该代码为基于带动量项的BP神经网络语音识别%% <html>% <table border="0" width="600px" id="table1"> <tr> <td><b><font size="2">该案例作者申明:</font></b></td> </tr> <tr><td><span class="comment"><font size="2">1:本人长期驻扎在此<a target="_blank" href="http://www.ilovematlab.cn/forum-158-1.html"><font color="#0000FF">板块</font></a>里,对该案例提问,做到有问必答。本套书籍官方网站为:<a href="http://video.ourmatlab.com">video.ourmatlab.com</a></font></span></td></tr><tr> <td><font size="2">2:点此<a href="http://union.dangdang.com/transfer/transfer.aspx?from=P-284318&backurl=http://www.dangdang.com/">从当当预定本书</a>:<a href="http://union.dangdang.com/transfer/transfer.aspx?from=P-284318&backurl=http://www.dangdang.com/">《Matlab神经网络30个案例分析》</a>。</td></tr><tr> <td><p class="comment"></font><font size="2">3</font><font size="2">:此案例有配套的教学视频,视频下载方式<a href="http://video.ourmatlab.com/vbuy.html">video.ourmatlab.com/vbuy.html</a></font><font size="2">。</font></p></td> </tr> <tr> <td><span class="comment"><font size="2"> 4:此案例为原创案例,转载请注明出处(《Matlab神经网络30个案例分析》)。</font></span></td> </tr> <tr> <td><span class="comment"><font size="2"> 5:若此案例碰巧与您的研究有关联,我们欢迎您提意见,要求等,我们考虑后可以加在案例里。</font></span></td> </tr> </table>% </html>%% 清空环境变量clcclear%% 训练数据预测数据提取及归一化%下载四类语音信号load data1 c1load data2 c2load data3 c3load data4 c4%四个特征信号矩阵合成一个矩阵data(1:500,:)=c1(1:500,:);data(501:1000,:)=c2(1:500,:);data(1001:1500,:)=c3(1:500,:);data(1501:2000,:)=c4(1:500,:);%从1到2000间随机排序k=rand(1,2000);[m,n]=sort(k);%输入输出数据input=data(:,2:25);output1 =data(:,1);%把输出从1维变成4维output=zeros(2000,4);for i=1:2000switch output1(i)case 1output(i,:)=[1 0 0 0];case 2output(i,:)=[0 1 0 0];case 3output(i,:)=[0 0 1 0];case 4output(i,:)=[0 0 0 1];endend%随机提取1500个样本为训练样本,500个样本为预测样本input_train=input(n(1:1500),:)';output_train=output(n(1:1500),:)';input_test=input(n(1501:2000),:)';output_test=output(n(1501:2000),:)';%输入数据归一化[inputn,inputps]=mapminmax(input_train);%% 网络结构初始化innum=24;midnum=25;outnum=4;%权值初始化w1=rands(midnum,innum);b1=rands(midnum,1);w2=rands(midnum,outnum);b2=rands(outnum,1);w2_1=w2;w2_2=w2_1;w1_1=w1;w1_2=w1_1;b1_1=b1;b1_2=b1_1;b2_1=b2;b2_2=b2_1;%学习率xite=0.1;alfa=0.01;loopNumber=10;I=zeros(1,midnum);Iout=zeros(1,midnum);FI=zeros(1,midnum);dw1=zeros(innum,midnum);db1=zeros(1,midnum);%% 网络训练E=zeros(1,loopNumber);for ii=1:10E(ii)=0;for i=1:1:1500%% 网络预测输出x=inputn(:,i);% 隐含层输出for j=1:1:midnumI(j)=inputn(:,i)'*w1(j,:)'+b1(j);Iout(j)=1/(1+exp(-I(j)));end% 输出层输出yn=w2'*Iout'+b2;%% 权值阀值修正%计算误差e=output_train(:,i)-yn;E(ii)=E(ii)+sum(abs(e));%计算权值变化率dw2=e*Iout;db2=e';for j=1:1:midnumS=1/(1+exp(-I(j)));FI(j)=S*(1-S);endfor k=1:1:innumfor j=1:1:midnumdw1(k,j)=FI(j)*x(k)*(e(1)*w2(j,1)+e(2)*w2(j,2)+e(3)*w2(j,3)+e(4)*w2(j,4));db1(j)=FI(j)*(e(1)*w2(j,1)+e(2)*w2(j,2)+e(3)*w2(j,3)+e(4)*w2(j,4));endendw1=w1_1+xite*dw1'+alfa*(w1_1-w1_2);b1=b1_1+xite*db1'+alfa*(b1_1-b1_2);w2=w2_1+xite*dw2'+alfa*(w2_1-w2_2);b2=b2_1+xite*db2'+alfa*(b2_1-b2_2);w1_2=w1_1;w1_1=w1;w2_2=w2_1;w2_1=w2;b1_2=b1_1;b1_1=b1;b2_2=b2_1;b2_1=b2;endend%% 语音特征信号分类inputn_test=mapminmax('apply',input_test,inputps);fore=zeros(4,500);for ii=1:1for i=1:500%1500%隐含层输出for j=1:1:midnumI(j)=inputn_test(:,i)'*w1(j,:)'+b1(j);Iout(j)=1/(1+exp(-I(j)));endfore(:,i)=w2'*Iout'+b2;endend%% 结果分析%根据网络输出找出数据属于哪类output_fore=zeros(1,500);for i=1:500output_fore(i)=find(fore(:,i)==max(fore(:,i)));end%BP网络预测误差error=output_fore-output1(n(1501:2000))';%画出预测语音种类和实际语音种类的分类图figure(1)plot(output_fore,'r')hold onplot(output1(n(1501:2000))','b')legend('预测语音类别','实际语音类别')%画出误差图figure(2)plot(error)title('BP网络分类误差','fontsize',12)xlabel('语音信号','fontsize',12)ylabel('分类误差','fontsize',12)%print -dtiff -r600 1-4k=zeros(1,4);%找出判断错误的分类属于哪一类for i=1:500if error(i)~=0[b,c]=max(output_test(:,i));switch ccase 1k(1)=k(1)+1;case 2k(2)=k(2)+1;case 3k(3)=k(3)+1;case 4k(4)=k(4)+1;endendend%找出每类的个体和kk=zeros(1,4);for i=1:500[b,c]=max(output_test(:,i));switch ccase 1kk(1)=kk(1)+1;case 2kk(2)=kk(2)+1;case 3kk(3)=kk(3)+1;case 4kk(4)=kk(4)+1;endend%正确率rightridio=(kk-k)./kk;disp('正确率')disp(rightridio);web browser www.matlabsky.com%%% <html>% <table width="656" align="left" > <tr><td align="center"><p><font size="2"><a href="http://video.ourmatlab.com/">Matlab神经网络30个案例分析</a></font></p><p align="left"><font size="2">相关论坛:</font></p><p align="left"><font size="2">《Matlab神经网络30个案例分析》官方网站:<a href="http://video.ourmatlab.com">video.ourmatlab.com</a></font></p><p align="left"><font size="2">Matlab技术论坛:<a href="http://www.matlabsky.com">www.matlabsky.com</a></font></p><p align="left"><font size="2">M</font><font size="2">atlab函数百科:<a href="http://www.mfun.la">www.mfun.la</a></font></p><p align="left"><font size="2">Matlab中文论坛:<a href="http://www.ilovematlab.com">www.ilovematlab.com</a></font></p></td> </tr></table>% </html>


4.基于PSO和BP网络的预测
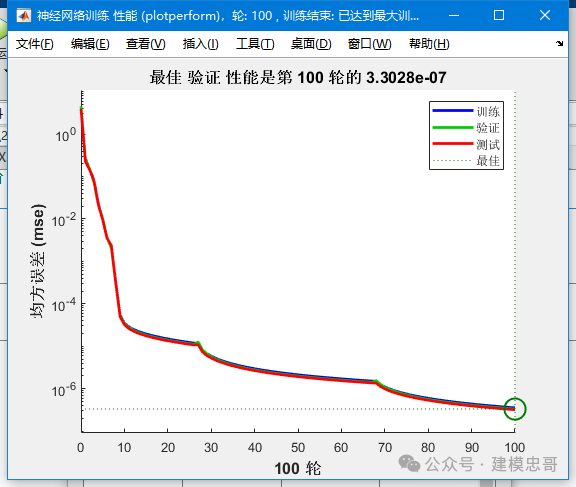
%% 该代码为基于PSO和BP网络的预测%%% 清空环境clcclear%读取数据load data input output%节点个数inputnum=2;hiddennum=5;outputnum=1;%训练数据和预测数据input_train=input(1:1900,:)';input_test=input(1901:2000,:)';output_train=output(1:1900)';output_test=output(1901:2000)';%选连样本输入输出数据归一化[inputn,inputps]=mapminmax(input_train);[outputn,outputps]=mapminmax(output_train);%构建网络net=newff(inputn,outputn,hiddennum);% 参数初始化%粒子群算法中的两个参数c1 = 1.49445;c2 = 1.49445;maxgen=100; % 进化次数sizepop=30; %种群规模Vmax=1;Vmin=-1;popmax=5;popmin=-5;for i=1:sizepoppop(i,:)=5*rands(1,21);V(i,:)=rands(1,21);fitness(i)=fun(pop(i,:),inputnum,hiddennum,outputnum,net,inputn,outputn);end% 个体极值和群体极值[bestfitness bestindex]=min(fitness);zbest=pop(bestindex,:); %全局最佳gbest=pop; %个体最佳fitnessgbest=fitness; %个体最佳适应度值fitnesszbest=bestfitness; %全局最佳适应度值%% 迭代寻优for i=1:maxgeni;for j=1:sizepop%速度更新V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));V(j,find(V(j,:)>Vmax))=Vmax;V(j,find(V(j,:)<Vmin))=Vmin;%种群更新pop(j,:)=pop(j,:)+0.2*V(j,:);pop(j,find(pop(j,:)>popmax))=popmax;pop(j,find(pop(j,:)<popmin))=popmin;%自适应变异pos=unidrnd(21);if rand>0.95pop(j,pos)=5*rands(1,1);end%适应度值fitness(j)=fun(pop(j,:),inputnum,hiddennum,outputnum,net,inputn,outputn);endfor j=1:sizepop%个体最优更新if fitness(j) < fitnessgbest(j)gbest(j,:) = pop(j,:);fitnessgbest(j) = fitness(j);end%群体最优更新if fitness(j) < fitnesszbestzbest = pop(j,:);fitnesszbest = fitness(j);endendyy(i)=fitnesszbest;end%% 结果分析plot(yy)title(['适应度曲线 ' '终止代数=' num2str(maxgen)]);xlabel('进化代数');ylabel('适应度');x=zbest;%% 把最优初始阀值权值赋予网络预测% %用遗传算法优化的BP网络进行值预测w1=x(1:inputnum*hiddennum);B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);net.iw{1,1}=reshape(w1,hiddennum,inputnum);net.lw{2,1}=reshape(w2,outputnum,hiddennum);net.b{1}=reshape(B1,hiddennum,1);net.b{2}=B2;%% BP网络训练%网络进化参数net.trainParam.epochs=100;net.trainParam.lr=0.1;%net.trainParam.goal=0.00001;%网络训练[net,per2]=train(net,inputn,outputn);%% BP网络预测%数据归一化inputn_test=mapminmax('apply',input_test,inputps);an=sim(net,inputn_test);test_simu=mapminmax('reverse',an,outputps);error=test_simu-output_test;web browser www.matlabsky.comweb browser http://www.matlabsky.com/thread-11198-1-1.html%%% <html>% <table width="656" align="left" > <tr><td align="center"><p><font size="2"><a href="http://video.ourmatlab.com/">Matlab神经网络30个案例分析</a></font></p><p align="left"><font size="2">相关论坛:</font></p><p align="left"><font size="2">《Matlab神经网络30个案例分析》官方网站:<a href="http://video.ourmatlab.com">video.ourmatlab.com</a></font></p><p align="left"><font size="2">Matlab技术论坛:<a href="http://www.matlabsky.com">www.matlabsky.com</a></font></p><p align="left"><font size="2">M</font><font size="2">atlab函数百科:<a href="http://www.mfun.la">www.mfun.la</a></font></p><p align="left"><font size="2">Matlab中文论坛:<a href="http://www.ilovematlab.com">www.ilovematlab.com</a></font></p></td> </tr></table>% </html>
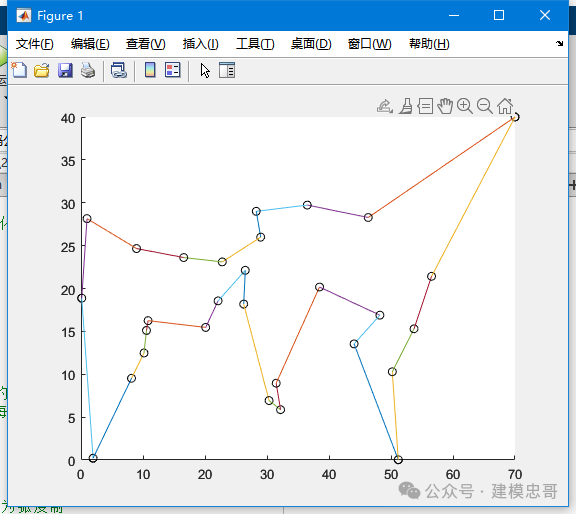
5.模拟退火算法
旅行商问题是一类经典的组合优化问题,目标是给定若干城市,旅行商需要找到一条从起点城市出发,经过每一个城市且仅经过一次,最后回到起点的最短路径。模拟退火算法解决旅行商问题,目标是在多个城市间找到一条最短路径。代码通过退火算法逐步优化初始解,利用蒙特卡洛模拟和退火过程使得解能跳出局部最优,最终找到全局最优解。
example_1.txt
53.71 15.30 51.17 00.03 46.33 28.28 30.33 06.9356.54 21.42 10.82 16.25 22.79 23.10 10.16 12.4820.11 15.46 01.95 00.21 26.50 22.12 31.48 08.9626.24 18.18 44.04 13.54 28.98 25.99 38.47 20.1728.27 29.00 32.19 05.87 36.49 29.73 00.97 28.1508.96 24.66 16.56 23.61 10.56 15.11 50.21 10.2908.15 09.53 22.11 18.56 00.12 18.87 48.21 16.89
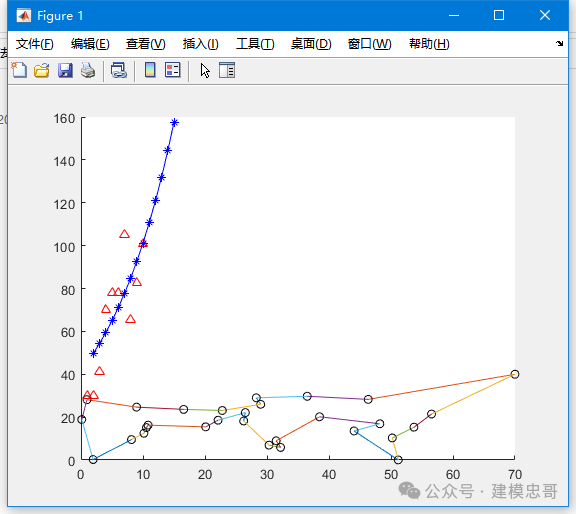
%% simulated_annealing% 模拟退火算法:适用于寻找全局最小值的优化问题clc, clear,close allload example_1.txtdata = example_1;x = data(:, 1:2:8); x = x(:);y = data(:, 2:2:8); y = y(:);[n, m] = size(data); % 返回数据的行数和列数(主要是需要行数)n = n * 4; % 每一行4个数据,一共有4n个点(再加上始末, 一共4n+2个点)data = [x y];d1 = [70, 40];data = [d1; data; d1]; % 始点与终点data = data * pi / 180; % 从角度制转化为弧度制distance = zeros(n+2); % 建立距离矩阵for i = 1:n+1for j = i + 1:n+2tmp = cos(data(i, 1) - data(j, 1)) * cos(data(i, 2)) * cos(data(j, 2)) + ...sin(data(i, 2)) * sin(data(j, 2));distance(i, j) = 6370 * acos(tmp);endenddistance = distance + distance';S0 = [ ];sum = inf; % 看实际数据情况修改为一个较大的数字% 使用蒙特卡洛模拟求得一个初始解rand('twister',5489);for j = 1:1000S = [1, 1+randperm(n), n+2]; % 长度为n+2的向量:第一位是1,中间是2到n+1的随机序列,最后一位是n+2tmp = 0;for i = 1:n+1tmp = tmp + distance(S(i), S(i+1));endif tmp < sumS0 = S; sum = tmp;endend% 设定初始值e = 0.1^30; % 终止温度L = 20000; % 循环次数alpha = 0.999; % 降温系数T = 1; % 初始温度% 退火过程for k = 1:L% 产生新解c = 2 + floor(n * rand(1, 2)); % 随机产生一个(2, n+2)之间的随机整数c = sort(c);c1 = c(1); c2 = c(2);% 计算函数代价delta = distance(S0(c1-1), S0(c2)) + distance(S0(c1), S0(c2+1)) - ...distance(S0(c1-1), S0(c1)) - distance(S0(c2), S0(c2+1));% 接收准则if delta < 0 || exp(-delta / T) > rand(1)S0 = [S0(1:c1-1), S0(c2:-1:c1), S0(c2+1:n+2)];sum = sum + delta;endT = T * alpha;if T < ebreak;endend% 输出巡航路径以及路径长度S0, sumdata = data * 180 / pi; % 从弧度制转换回角度制hold onfor i = 1: n + 1scatter(data(S0(i), 1), data(S0(i), 2), 'k');plot([data(S0(i), 1), data(S0(i+1), 1)],[data(S0(i), 2), data(S0(i+1), 2)]);endplot([data(S0(n+1), 1), data(S0(n+2), 1)],[data(S0(n+1), 2), data(S0(n+2), 2)]);
1. 旅行商问题(TSP)
-
经典的路径优化问题,要求找到一个城市巡回路径,使得总路径长度最短。模拟退火通过随机扰动当前解(如交换两城市顺序)来寻找最优路径。
2. 任务调度问题
-
模拟退火可以应用于作业车间调度问题(Job Shop Scheduling Problem, JSSP),解决在多个机器上调度多个任务,最小化总完成时间(Makespan)等目标。
3. 网络优化
-
在网络设计、路由优化等问题中,模拟退火可以寻找优化的网络拓扑结构或高效的路由路径。尤其在大规模通信网络中,它可用于解决多条路径的最优路由问题。
4. 图像处理与计算机视觉
-
图像分割:模拟退火可以用于优化分割后的区域,使得分割结果满足一定的目标函数,比如最大化类间方差等。
-
图像去噪:可以用于确定去噪的最佳参数,以在去除噪声的同时尽量保持图像的清晰度。
-
立体匹配:在立体视觉中,用于寻找视差图的全局最优解。
5. 神经网络的权重优化
-
模拟退火算法可以用于神经网络的权重初始化和优化,通过调整神经网络的权重以找到更好的收敛效果和最优权重组合,避免陷入局部最优。
6. 函数优化
-
在高维函数优化问题中,特别是具有多个局部极值点的非凸函数,模拟退火可通过随机跳跃避免陷入局部极值,从而找到全局最优值。
7. 结构优化
-
天线设计:通过模拟退火算法优化天线的形状和尺寸,以获得最佳性能。
-
建筑设计:应用于优化建筑结构、材料使用等,寻求在有限成本下的最佳结构设计方案。
8. 参数估计与模型拟合
-
模拟退火可以用于寻找复杂模型的最佳参数组合,如机器学习模型中的超参数调优,通过模拟退火搜索最优参数组合,以最大化模型性能。
9. 组合优化
-
背包问题:在背包问题中,模拟退火可用于寻找物品的最优选择组合,使得背包的总价值最大化且不超出容量限制。
-
分配问题:如资源分配、人员分配等,通过模拟退火找到最优的分配方式,满足一定的约束条件。
10. 分子结构优化与药物设计
-
在化学和生物信息学领域,模拟退火算法可以用于分子结构优化,寻找低能量稳定结构;在药物设计中,它可以帮助优化药物分子的构型和排列。
11. 金融优化问题
-
在金融领域,模拟退火可以应用于投资组合优化,寻找收益最大、风险最小的投资组合配置方式,或者用于期权定价等金融工程问题中的优化。
12. 物流与供应链优化
-
模拟退火可用于物流配送中的路径优化、仓库选址等问题。通过不断调整方案寻找最低成本和最佳效率的方案。
13. 基因序列比对
-
在生物信息学中,模拟退火可以用于寻找最优的基因序列比对方案,从而找到两个基因序列之间的最优匹配。
14. 城市规划与交通优化
-
在城市规划中,模拟退火算法可用于交通流量优化,例如优化信号灯配置,减少交通堵塞,或者规划最优的公共交通路线。
15. 电力系统优化
-
应用于电力系统中的电网优化,模拟退火可以帮助优化电力网络中的节点连接,以减少损耗并提高电力传输的效率。
总结:
模拟退火算法由于其跳出局部最优的能力和全局优化的效果,广泛应用于各种复杂的优化问题,尤其是在无法通过传统确定性方法有效求解的问题上。
6.灰色预测
%Matlab的灰色预测程序:%y=input('请输入数据');clc;cleary=[29.8 30.11 41.05 70.12 77.79 77.79 104.82 65.22 82.7 100.79]n=length(y);yy=ones(n,1);yy(1)=y(1);for i=2:nyy(i)=yy(i-1)+y(i)endB=ones(n-1,2);for i=1:(n-1)B(i,1)=-(yy(i)+yy(i+1))/2;B(i,2)=1;endBT=B';for j=1:(n-1)YN(j)=y(j+1);endYN=YN';A=inv(BT*B)*BT*YN;a=A(1);u=A(2);t=u/a;t_test=input('输入需要预测的个数');i=1:t_test+n;yys(i+1)=(y(1)-t).*exp(-a.*i)+t;yys(1)=y(1);for j=n+t_test:-1:2ys(j)=yys(j)-yys(j-1);endx=1:n;xs=2:n+t_test;yn=ys(2:n+t_test);plot(x,y,'^r',xs,yn,'*-b');det=0;for i=2:ndet=det+abs(yn(i)-y(i));enddet=det/(n-1);disp(['百分绝对误差为:',num2str(det),'%']);disp(['预测值为:',num2str(ys(n+1:n+t_test))]);%请输入数据 [29.8 30.11 41.05 70.12 77.79 77.79 104.82 65.22 82.7 100.79]

7.偏最小二乘回归
%% I. 清空环境变量clear allclc%% II. 导入数据load spectra;%% III. 随机划分训练集与测试集temp = randperm(size(NIR, 1));% temp = 1:60;%%% 1. 训练集——50个样本P_train = NIR(temp(1:50),:);T_train = octane(temp(1:50),:);%%% 2. 测试集——10个样本P_test = NIR(temp(51:end),:);T_test = octane(temp(51:end),:);%% IV. PLS回归模型%%% 1. 创建模型k = 2;[Xloadings,Yloadings,Xscores,Yscores,betaPLS,PLSPctVar,MSE,stats] = plsregress(P_train,T_train,k);%%% 2. 主成分贡献率分析figurepercent_explained = 100 * PLSPctVar(2,:) / sum(PLSPctVar(2,:));pareto(percent_explained)xlabel('主成分')ylabel('贡献率(%)')title('主成分贡献率')%%% 3. 预测拟合N = size(P_test,1);T_sim = [ones(N,1) P_test] * betaPLS;%% V. 结果分析与绘图%%% 1. 相对误差errorerror = abs(T_sim - T_test) ./ T_test;%%% 2. 决定系数R^2R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));%%% 3. 结果对比result = [T_test T_sim error]%%% 4. 绘图figureplot(1:N,T_test,'b:*',1:N,T_sim,'r-o')legend('真实值','预测值','location','best')xlabel('预测样本')ylabel('辛烷值')string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};title(string)
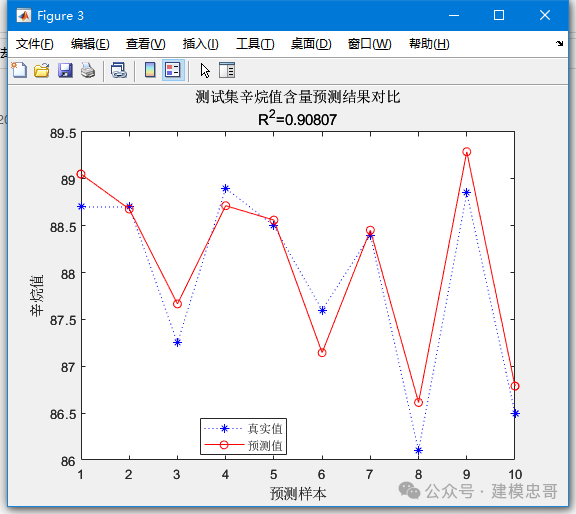
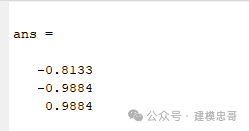
8.主成分回归
%% I. 清空环境变量clear allclc%% II. 导入数据load spectra;%% III. 随机划分训练集与测试集temp = randperm(size(NIR, 1));% temp = 1:60;%%% 1. 训练集——50个样本P_train = NIR(temp(1:50),:);T_train = octane(temp(1:50),:);%%% 2. 测试集——10个样本P_test = NIR(temp(51:end),:);T_test = octane(temp(51:end),:);%% IV. 主成分分析%%% 1. 主成分贡献率分析[PCALoadings,PCAScores,PCAVar] = princomp(NIR);figurepercent_explained = 100 * PCAVar / sum(PCAVar);pareto(percent_explained)xlabel('主成分')ylabel('贡献率(%)')title('主成分贡献率')%%% 2. 第一主成分vs.第二主成分[PCALoadings,PCAScores,PCAVar] = princomp(P_train);figureplot(PCAScores(:,1),PCAScores(:,2),'r+')hold on[PCALoadings_test,PCAScores_test,PCAVar_test] = princomp(P_test);plot(PCAScores_test(:,1),PCAScores_test(:,2),'o')xlabel('1st Principal Component')ylabel('2nd Principal Component')legend('Training Set','Testing Set','location','best')%% V. 主成分回归模型%%% 1. 创建模型k = 4;betaPCR = regress(T_train-mean(T_train),PCAScores(:,1:k));betaPCR = PCALoadings(:,1:k) * betaPCR;betaPCR = [mean(T_train)-mean(P_train) * betaPCR;betaPCR];%%% 2. 预测拟合N = size(P_test,1);T_sim = [ones(N,1) P_test] * betaPCR;%% VI. 结果分析与绘图%%% 1. 相对误差errorerror = abs(T_sim - T_test) ./ T_test;%%% 2. 决定系数R^2R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));%%% 3. 结果对比result = [T_test T_sim error]%%% 4. 绘图figureplot(1:N,T_test,'b:*',1:N,T_sim,'r-o')legend('真实值','预测值','location','best')xlabel('预测样本')ylabel('辛烷值')string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};title(string)
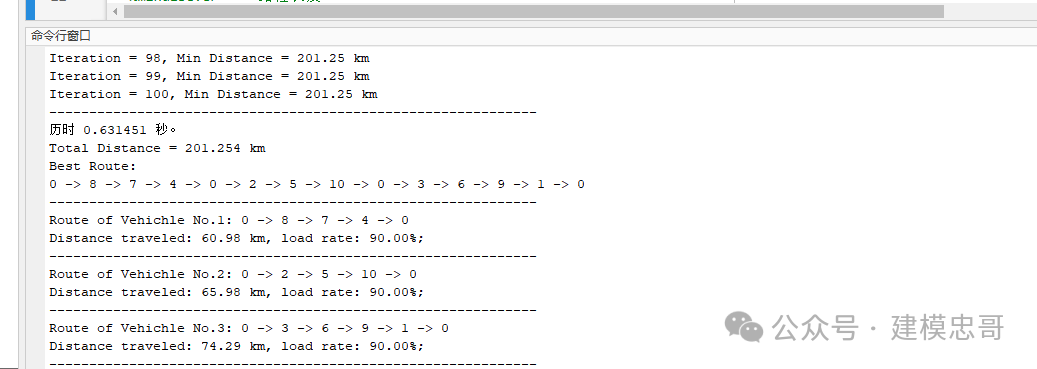
9.蚁群算法求最短路径
clc %清空命令行窗口clear %从当前工作区中删除所有变量,并将它们从系统内存中释放close all %删除其句柄未隐藏的所有图窗tic % 保存当前时间%% 蚁群算法求解CDVRP%输入:%City 需求点经纬度%Distance 距离矩阵%Demand 各需求点需求量%AntNum 种群个数%Alpha 信息素重要程度因子%Beta 启发函数重要程度因子%Rho 信息素挥发因子%Q 常系数%Eta 启发函数%Tau 信息素矩阵%MaxIter 最大迭代次数%输出:%bestroute 最短路径%mindisever 路径长度%% 加载数据load('../test_data/City.mat') %需求点经纬度,用于画实际路径的XY坐标load('../test_data/Distance.mat') %距离矩阵load('../test_data/Demand.mat') %需求量load('../test_data/Travelcon.mat') %行程约束load('../test_data/Capacity.mat') %车容量约束%% 初始化问题参数CityNum = size(City,1)-1; %需求点个数%% 初始化参数AntNum = 8; % 蚂蚁数量Alpha = 1; % 信息素重要程度因子Beta = 5; % 启发函数重要程度因子Rho = 0.1; % 信息素挥发因子Q = 1; % 常系数Eta = 1./Distance; % 启发函数Tau = ones(CityNum+1); % (CityNum+1)*(CityNum+1)信息素矩阵 初始化全为1Population = zeros(AntNum,CityNum*2+1); % AntNum行,(CityNum*2+1)列 的路径记录表MaxIter = 100; % 最大迭代次数bestind = ones(1,CityNum*2+1); % 各代最佳路径MinDis = zeros(MaxIter,1); % 各代最佳路径的长度%% 迭代寻找最佳路径Iter = 1; % 迭代次数初值while Iter <= MaxIter %当未到达最大迭代次数%% 逐个蚂蚁路径选择for i = 1:AntNumTSProute=2:CityNum+1; %生成一条顺序不包括首尾位的升序TSP路线VRProute=[]; %初始化VRP路径while ~isempty(TSProute)%开辟新的子路径subpath=1; %先将配送中心放入子路径起点DisTraveled=0; %此子路径的距离初始化为零delivery=0; %此子路径的车辆可配送量初始化为零delete=subpath; %delete(end)=1给第一次进入内while的P(k)首项用while ~isempty(TSProute) %为子路径subpath第二个及以后的位置安排需求点%% 计在内while中计算城市间转移概率P = TSProute; % 为轮盘赌选择建立等于剩余需经过城市数量的长度的向量for k = 1:length(TSProute)%delete(end)为刚刚经过的城市,TSProute(k)为剩余可能经过的城市P(k) = Tau(delete(end),TSProute(k))^Alpha * Eta(delete(end),TSProute(k))^Beta; %省略相同分母endP = P/sum(P);% 轮盘赌法选择下一个访问城市Pc = cumsum(P); %累加概率TargetIndex = find(Pc >= rand); %寻找左数第一个大于伪随机数的累加概率的索引target = TSProute(TargetIndex(1)); %此索引对应的城市%不要强行改变蚂蚁通过轮盘法选到的下一个城市%它选到就确定了,然后如果超约束,结束此subpath%判断行程约束if delivery+Demand(target) > Capacity || DisTraveled+Distance(delete(end),target)+Distance(target,1) > TravelconbreakelseDisTraveled=DisTraveled+Distance(delete(end),target); %若符合,则经过的距离累加此距离delivery = delivery+Demand(target);%此点加入子路径subpath=[subpath,target];%此点加入要删除的点序列delete=[delete,target];%TSP路径中排除已安排的城市TSProute=setdiff(TSProute,delete);endend %内while结束,此subpath结束%直接在VRProute后面填充这条子路径VRProute=[VRProute,subpath];end %外while结束,此VRProute完整%在VRProute后未到CityNum*2+1的空位填入1fillwithones = linspace(1,1,CityNum*2+1-length(VRProute));VRProute=[VRProute,fillwithones];%把成型的VRP路径赋给种群矩阵Population(i,:)=VRProute;end%% 计算各个蚂蚁的路径距离ttlDistance = zeros(AntNum,1); %预分配内存for i = 1:AntNumDisTraveled=0; % 蚂蚁子路径已经过的距离delivery=0; % 汽车已经送货量,即已经到达点的需求量之和Dis=0; %此蚂蚁所有子路径的总距离route = Population(i,:); %单独取出一只蚂蚁的路线for j=2:length(route)DisTraveled = DisTraveled+Distance(route(j-1),route(j)); %每两点间距离累加delivery = delivery+Demand(route(j)); %累加可配送量if DisTraveled > Travelcon || delivery > CapacityDis = Inf; %对非可行解进行惩罚breakendif route(j)==1 %若此位是配送中心Dis=Dis+DisTraveled; %累加已行驶距离DisTraveled=0; %已行驶距离置零delivery=0; %已配送置零endendttlDistance(i)=Dis; %存储此方案总距离end%% 存储历史最优信息if Iter == 1 %若是第一次迭代 不需要与上次迭代结果对比[min_Length,min_index] = min(ttlDistance); %取得此次迭代最短距离MinDis(Iter) = min_Length; %存储此次迭代最优路线的距离bestind = Population(min_index,:); %存储此次迭代最优路径else[min_Length,min_index] = min(ttlDistance); %取得此次迭代最短距离MinDis(Iter) = min(MinDis(Iter-1),min_Length); %与上次迭代结果对比if min_Length == MinDis(Iter) %若此代最短距离是在此代中出现bestind = Population(min_index,:); %此代最短距离对应的路径赋给此代最优路径endend%% 更新信息素Delta_Tau = zeros(CityNum+1,CityNum+1); %预分配内存% 逐个蚂蚁计算for i = 1:AntNum% 逐个城市计算for j = 1:size(Population,2)-1%所有蚂蚁从i到j的信息素累积和:用这一点Delta_Tau之前的值加上新值等于现在的信息素浓度Delta_Tau(Population(i,j),Population(i,j+1)) = Delta_Tau(Population(i,j),Population(i,j+1)) + Q/ttlDistance(i);endendTau = (1-Rho)*Tau+Delta_Tau; %对信息素矩阵进行整体计算,减去挥发,加上新生成的信息素%% 显示此代信息fprintf('Iteration = %d, Min Distance = %.2f km \n',Iter,MinDis(Iter))%% 更新迭代次数Iter = Iter+1; %迭代次数加1%Population = zeros(AntNum,CityNum*2+1); %清空路径记录表end%% 找出历史最短距离和对应路径mindisever = MinDis(MaxIter); % 取得历史最优适应值的位置、最优目标函数值bestroute = bestind; % 取得最优个体%删去路径中多余1for i=1:length(bestroute)-1if bestroute(i)==bestroute(i+1) %相邻位都为1时bestroute(i)=0; %前一个置零endendbestroute(bestroute==0)=[]; %删去多余零元素bestroute=bestroute-1; % 编码各减1,与文中的编码一致%% 计算结果数据输出到命令行disp('-------------------------------------------------------------')toc %显示运行时间fprintf('Total Distance = %s km \n',num2str(mindisever))TextOutput(Distance,Demand,bestroute,Capacity) %显示最优路径disp('-------------------------------------------------------------')%% 迭代图figureplot(MinDis,'LineWidth',2) %展示目标函数值历史变化xlim([1 Iter-1]) %设置 x 坐标轴范围set(gca, 'LineWidth',1)xlabel('Iterations')ylabel('Min Distance(km)')title('ACO Process')%% 绘制实际路线DrawPath(bestroute,City)

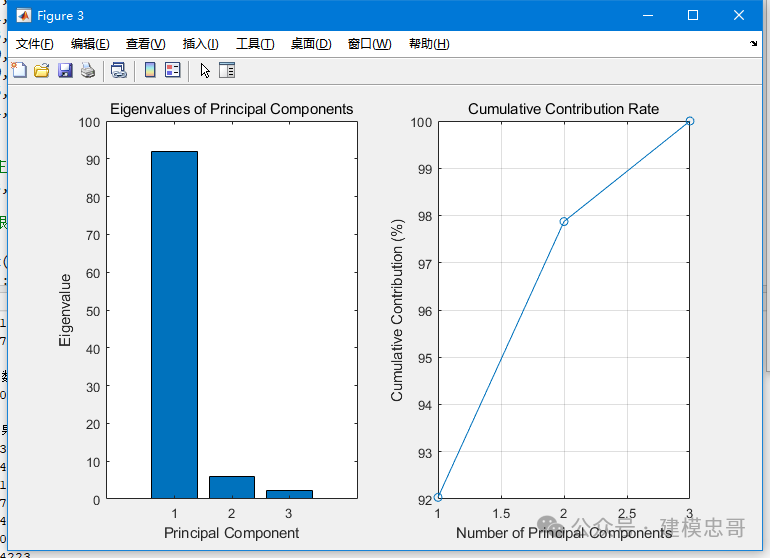
10.主成分分析:
% 示例调用代码% 生成一些测试数据,5个样本,3个特征(指标变量)h = [2.5, 2.4, 1.0;0.5, 0.7, 0.5;2.2, 2.9, 1.5;1.9, 2.2, 1.7;3.1, 3.0, 2.0;2.3, 2.7, 1.8;2.0, 1.6, 1.2;1.0, 1.1, 0.8;1.5, 1.6, 1.2;1.1, 0.9, 0.6;];% 调用主成分分析算法[tg, xs, q, px, newdt] = pca(h);% 显示输出结果disp('特征根及贡献率:');disp(tg);disp('选择的主成分系数:');disp(xs);disp('主成分综合评价模型系数:');disp(q);% 如果进行了主成分综合评价,还会显示排序结果if ~isempty(px)disp('主成分综合评价排序结果:');disp(px);end
function [tg xs q px newdt]=pca(h) %输入只能是以分析的指标变量为列,样本变量为行的数据!h=zscore(h); %数据标准化r=corrcoef(h); %计算相关系数矩阵disp('计算的相关系数矩阵如下:');disp(r);[x,y,z]=pcacov(r); %计算特征向量与特征值s=zeros(size(z));for i=1:length(z)s(i)=sum(z(1:i));enddisp('由上计算出相关系数矩阵的前几个特征根及其贡献率:');disp([z,s])tg=[z,s];f=repmat(sign(sum(x)),size(x,1),1);x=x.*f;n=input('请选择前n个需要计算的主成分:\n');disp('由此可得选择的主成分系数分别为:');for i=1:nxs(i,:)=(x(:,i)');endnewdt=h*xs';disp('以主成分的贡献率为权重,构建主成分综合评价模型系数:');q=((z(1:n)./100)')w=input('是否需要进行主成分综合评价?(y or n)\n');if w==ydf=h*x(:,1:n);tf=df*z(1:n)/100;[stf,ind]=sort(tf,'descend'); %按照降序排列disp('主成分综合评价结果排序:');px=[ind,stf]elsereturn;end

常见的最优化算法:
1.约束优化问题:
-
minRosen(Rosen梯度法求解约束多维函数的极值)(算法还有bug)
-
minPF(外点罚函数法解线性等式约束)
-
minGeneralPF(外点罚函数法解一般等式约束)
-
minNF(内点罚函数法)
-
minMixFun(混合罚函数法)
-
minJSMixFun(混合罚函数加速法)
-
minFactor(乘子法)
-
minconPS(坐标轮换法)(算法还有bug)
-
minconSimpSearch(复合形法)
2.非线性最小二乘优化问题
-
minMGN(修正G-N法)
3.线性规划:
-
CmpSimpleMthd(完整单纯形法)
4.整数规划(含0-1规划)
-
DividePlane(割平面法)
-
ZeroOneprog(枚举法)
5.二次规划
-
QuadLagR(拉格朗日法)
-
ActivedeSet(起作用集法)
6.辅助函数(在一些函数中会调用)
-
minNT(牛顿法求多元函数的极值)
-
Funval(求目标函数的值)
-
minMNT(修正的牛顿法求多元函数极值)
-
minHJ(黄金分割法求一维函数的极值)
7.高级优化算法
1)粒子群优化算法(求解无约束优化问题)
-
1>PSO(基本粒子群算法)
-
2>YSPSO(待压缩因子的粒子群算法)
-
3>LinWPSO(线性递减权重粒子群优化算法)
-
4>SAPSO(自适应权重粒子群优化算法)
-
5>RandWSPO(随机权重粒子群优化算法)
-
6>LnCPSO(同步变化的学习因子)
-
7>AsyLnCPSO(异步变化的学习因子)(算法还有bug)
-
8>SecPSO(用二阶粒子群优化算法求解无约束优化问题)
-
9>SecVibratPSO(用二阶振荡粒子群优化算法求解五约束优化问题)
-
10>CLSPSO(用混沌群粒子优化算法求解无约束优化问题)
-
11>SelPSO(基于选择的粒子群优化算法)
-
12>BreedPSO(基于交叉遗传的粒子群优化算法)
-
13>SimuAPSO(基于模拟退火的粒子群优化算法)
2)遗传算法
-
1>myGA(基本遗传算法解决一维约束规划问题)
-
2>SBOGA(顺序选择遗传算法求解一维无约束优化问题)
-
3>NormFitGA(动态线性标定适应值的遗传算法求解一维无约束优化问题)
-
4>GMGA(大变异遗传算法求解一维无约束优化问题)
-
5>AdapGA(自适应遗传算法求解一维无约束优化问题)
-
6>DblGEGA(双切点遗传算法求解一维无约束优化问题)
-
7>MMAdapGA(多变异位自适应遗传算法求解一维无约束优化问题)

11.离散Hopfield的分类——高校科研能力评价
%% 离散Hopfield的分类——高校科研能力评价%% 清空环境变量clear allclc%% 导入记忆模式T = [-1 -1 1; 1 -1 1]';%% 权值和阈值学习[S,Q] = size(T);Y = T(:,1:Q-1) - T(:,Q)*ones(1,Q-1);[U,SS,V] = svd(Y);K = rank(SS);TP = zeros(S,S);for k = 1:KTP = TP + U(:,k)*U(:,k)';endTM = zeros(S,S);for k = K+1:STM = TM + U(:,k)*U(:,k)';endtau = 10;Ttau = TP - tau*TM;Itau = T(:,Q) - Ttau*T(:,Q);h = 0.15;C1 = exp(h)-1;C2 = -(exp(-tau*h) - 1)/tau;w = expm(h*Ttau);b = U * [ C1*eye(K) zeros(K,S-K);zeros(S-K,K) C2*eye(S-K)] * U' * Itau;%% 导入待记忆的模式Ai = [-0.7; -0.6; 0.6];y0 = Ai;%% 迭代计算for i = 1:5for j = 1:size(y0,1)y{i}(j,:) = satlins(w(j,:)*y0 + b(j));endy0 = y{i};endy{1}
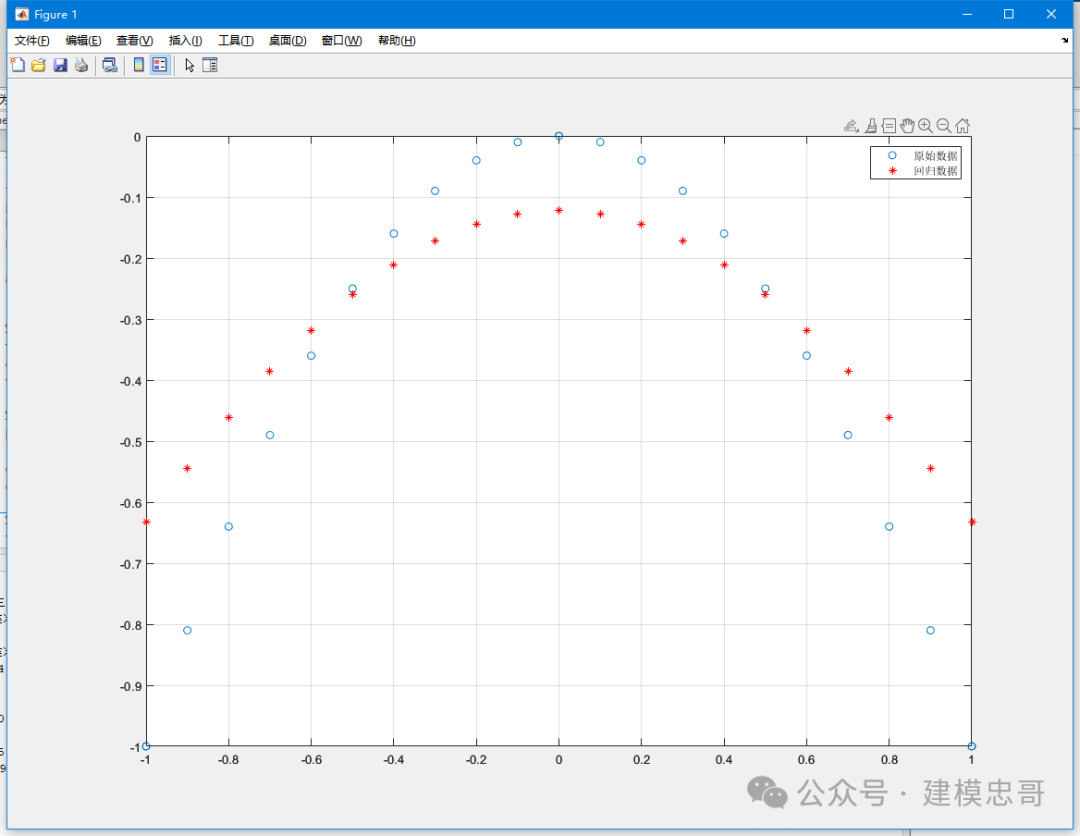
12.SVM分类与回归
%% A Little Clean Worktic;clear;clc;close all;format compact;%% 使用SVM进行分类的小例子%{一个班级里面有两个男生(男生1、男生2),两个女生(女生1、女生2),其中男生1 身高:176cm 体重:70kg;男生2 身高:180cm 体重:80kg;女生1 身高:161cm 体重:45kg;女生2 身高:163cm 体重:47kg;如果我们将男生定义为1,女生定义为-1,并将上面的数据放入矩阵data中,并在label中存入男女生类别标签(1、-1)%}% 数据data = [176 70;180 80;161 45;163 47];label = [1;1;-1;-1]; % 1表示男,-1表示女% 使用fitcsvm建立分类模型model = fitcsvm(data, label);% 新数据预测testdata = [190 85];[predictlabel, score] = predict(model, testdata);% 显示预测结果disp(['预测标签: ', num2str(predictlabel)]);if predictlabel == 1disp('==该生为男生');elseif predictlabel == -1disp('==该生为女生');end%% 使用fitcsvm测试heart_scale数据集% 首先载入数据load heart_scale;data = heart_scale_inst;label = heart_scale_label;% 选取前200个数据作为训练集合,后70个数据作为测试集合ind = 200;traindata = data(1:ind,:);trainlabel = label(1:ind,:);testdata = data(ind+1:end,:);testlabel = label(ind+1:end,:);% 利用训练集合建立分类模型model = fitcsvm(traindata, trainlabel, 'KernelFunction', 'rbf', 'BoxConstraint', 1.2, 'KernelScale', 2.8);% 在训练集合上测试模型[ptrain, score_train] = predict(model, traindata);disp('训练集合分类准确率:');train_accuracy = sum(ptrain == trainlabel) / length(trainlabel) * 100;disp(train_accuracy);% 在测试集合上测试模型[ptest, score_test] = predict(model, testdata);disp('测试集合分类准确率:');test_accuracy = sum(ptest == testlabel) / length(testlabel) * 100;disp(test_accuracy);%% 使用SVM进行回归的小例子% 生成待回归的数据x = (-1:0.1:1)';y = -x.^2;% 使用fitrsvm建立回归模型model = fitrsvm(x, y, 'KernelFunction', 'rbf', 'BoxConstraint', 2.2, 'KernelScale', 2.8, 'Epsilon', 0.01);% 调用 predict 进行回归预测py = predict(model, x); % 去掉 ~ 仅返回一个输出% 绘图部分保持不变scrsz = get(0,'ScreenSize');figure('Position',[scrsz(3)*1/4 scrsz(4)*1/6 scrsz(3)*4/5 scrsz(4)]*3/4);plot(x, y, 'o');hold on;plot(x, py, 'r*');legend('原始数据', '回归数据');grid on;% 进行预测testx = 1.1;disp('真实数据');testy = -testx.^2% 使用模型预测ptesty = predict(model, testx);disp('预测数据');disp(ptesty);%% Record Timetoc;
原文地址:https://blog.csdn.net/weixin_43608857/article/details/142392896
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
