代码随想录算法训练营第6天 | 242.有效的字母异位词 , 349. 两个数组的交集 , 202. 快乐数 , 1. 两数之和
哈希知识基础
242.有效的字母异位词
题目链接:https://leetcode.cn/problems/valid-anagram/description/
使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
思路:简易的哈希表
设置一个数组,其实就是一个简单哈希表,大小为26 就可以了,初始化为0,因为字符a到字符z的ASCII也是26个连续的数值。
这个数组用来记录字符串s里字符出现的次数,把字符映射到数组也就是哈希表的索引下标上。
只需要分别的遍历一下两个字符串,遍历第一个字符串的时候,对应的位置+1;遍历第二个字符串的时候,对应的位置-1。
最后检查一下,如果数组里有的元素不为0,说明一定是谁多了字符或者谁少了字符,return false
如果数组里所有的元素都为0,说明找到了,return true
class Solution {
public boolean isAnagram(String s, String t) {
int[] a = new int[26];
if(s.length()!=t.length())
return false;
for(int i=0;i<s.length();i++){
a[s.charAt(i)-'a'] ++;
}
for(int i=0;i<t.length();i++){
a[t.charAt(i)-'a'] --;
}
for(int count:a)
{
if(count!=0)
return false;
}
return true;
}
}
时间复杂度 O(n)
空间复杂度 O(1)
349. 两个数组的交集
题目连接:https://leetcode.cn/problems/intersection-of-two-arrays/description/
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。尝试用一遍扫描实现。
解法:使用HashSet
这道题目,主要要学会使用HashSet求解即可。
但是要注意,使用数组来做哈希的题目,是因为题目都限制了数值的大小。
而这道题目没有限制数值的大小,就无法使用数组来做哈希表了。
而且如果哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set1 = new HashSet<>();
Set<Integer> resSet = new HashSet<>();
for(int val:nums1)
set1.add(val);
for(int val:nums2)
{
if(set1.contains(val))
resSet.add(val);
}
// 方法1:直接转成数组
// return resSet.stream().mapToInt(x->x).toArray();
// 方法2:定义一个数组
int[] arr = new int[resSet.size()];
int j = 0;
for(int val:resSet){
arr[j++] = val;
}
return arr;
}
}
时间复杂度 O(m+n)
空间复杂度 O(m+n) ,其中 m 和 n 分别是两个数组的长度。
202. 快乐数
题目连接:https://leetcode.cn/problems/happy-number/description/
解法:哈希法快速判断
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了。
题目中说了会 无限循环,那么也就是说求和的过程中,sum会重复出现,这对解题很重要。
还有一个难点就是求和的过程,如果对取数值各个位上的单数操作不熟悉的话,做这道题也会比较艰难。
class Solution {
public int getSum(int n){
int ans = 0;
// 不能写n%10,假如是100就直接不执行了
while(n >0){
ans += (n%10)*(n%10);
n = n/10;
}
return ans;
}
public boolean isHappy(int n) {
int result = n;
Set<Integer>set = new HashSet<>();
// 循环
// while(true){
// result = getSum(result);
// System.out.println(result);
// if(result==1)
// return true;
// else if(set.contains(result))
// return false;
// else
// set.add(result);
// }
// 第二种循环写法
while(n!=1 && !set.contains(n)){
set.add(n);
n = getSum(n);
}
return n==1;
}
}
时间复杂度:O(logn)
空间复杂度:O(logn)
1. 两数之和
题目连接:https://leetcode.cn/problems/two-sum/
解法:哈希法
很明显暴力的解法是两层for循环查找,时间复杂度是O(n^2)。
当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
因为本题,我们不仅要知道元素有没有遍历过,还要知道这个元素对应的下标,需要使用 key value结构来存放,key来存元素,value来存下标,那么使用map正合适。
再来看一下使用数组和set来做哈希法的局限。
(1)数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
(2)set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
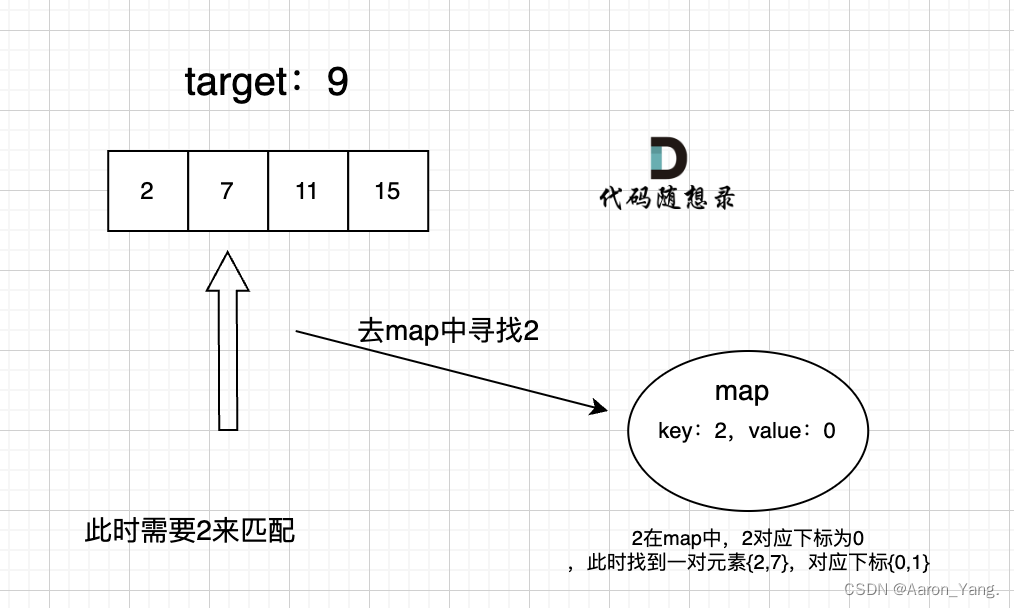
map目的用来存放我们访问过的元素,因为遍历数组的时候,需要记录我们之前遍历过哪些元素和对应的下标,这样才能找到与当前元素相匹配的(也就是相加等于target)
map中的存储结构为 {key:数据元素,value:数组元素对应的下标}
在遍历数组的时候,只需要向map去查询是否有和目前遍历元素匹配的数值,如果有,就找到的匹配对,如果没有,就把目前遍历的元素放进map中,因为map存放的就是我们访问过的元素。
class Solution {
public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
Map<Integer,Integer>map = new HashMap<>();
for(int i=0;i<nums.length;i++){
int tmp = target-nums[i];
if(map.containsKey(tmp))
{
res[0] = map.get(tmp);
res[1] = i;
return res;
}else{
map.put(nums[i],i);
}
}
return res;
}
}
时间复杂度:O(n)
空间复杂度:O(n)
原文地址:https://blog.csdn.net/Captain_Aaron/article/details/135597958
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
