Linux 红黑树内核源码剖析

🕗 发布于 2024-07-23 14:00 linux c语言 内核

Linux 红黑树内核源码剖析

1. 数据结构红黑树

在学习数据结构红黑树之前建议先看我的数据结构之红黑树(C++实现)的理论部分。

2. 红黑树

2.1 红黑树的概念

红黑树也是一种二叉搜索树，在此基础上每个结点增加一个存储位表示结点的颜色，可以是红色或者黑色，通过对任何一条从根结点到叶子结点的路径上每个结点颜色的限制，红黑树确保没有一条路径会比其他路径大一倍，因此，是接近平衡的一颗二叉搜索树。

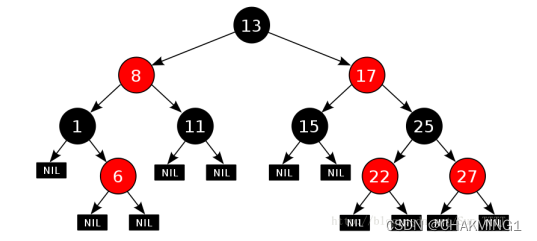
在这里插入图片描述

2.2 红黑树的性质

每个结点的颜色不是红色就是黑色。
根结点是黑色的。
如果一个结点是红色的，那么它的两个孩子结点是黑色的。
对于每个结点，从该结点到其所有后代的叶子结点的路径上，均包含相同数目的黑色结点。
每个叶子结点都是黑色的**(指的是空结点)**。

3. Linux内核红黑树的设计

本文章的设计可能与实际内核代码(不同版本)有些许差异，但整体实现思想一致。

3.1 结构介绍

#defineRB_RED0
#defineRB_BLACK1

struct rb_node {

unsigned long  __rb_parent_color;  // 最后一位保存颜色信息，其余位表示父结点的地址

    struct rb_node *rb_right;          // 右儿子

struct rb_node *rb_left;           // 左儿子

} __attribute__((aligned(sizeof(long)))); // 保证按照4字节或者8字节对齐

// 根结点
struct rb_root {
struct rb_node *rb_node;
};

这里的思想很巧妙，为了节省内存，我们的__rb_parent_color成员不止保存了父结点的地址还保存了当前的颜色信息。由于按照long类型大小进行内存对齐，所以地址的低2位或者4位均为0，这时候在存储父结点的地址的情况下，低位还可以保存当前结点的颜色信息。

3.2 宏介绍

下面的宏是为了方便进行结点操作。

#define offsetof(TYPE, MEMBER)  ((size_t)&((TYPE *)0)->MEMBER)

/**
 * container_of - cast a member of a structure out to the containing structure
 * @ptr:        the pointer to the member.
 * @type:       the type of the container struct this is embedded in. 
 * @member:     the name of the member within the struct.
 *
 */
// 通过某个成员获取type结构体的指针
// 这里的思想与Linux内核中链表设计思想相符合，是为了设计让红黑树可以应用在任何结构体中
#define container_of(ptr, type, member) ({                      \
       const typeof( ((type *)0)->member ) *__mptr = (ptr);    \
       (type *)( (char *)__mptr - offsetof(type,member) );})

// 清除末尾的颜色信息，拿到父结点的rb_node*结点
#define rb_parent(r)   ((struct rb_node *)((r)->__rb_parent_color & ~3))
// 创建一个空的ROOT结点
#define RB_ROOT(struct rb_root) { NULL, }

// 当一个结点为空时，父结点保存的是自身的地址
/* 'empty' nodes are nodes that are known not to be inserted in an rbtree */
#define RB_EMPTY_NODE(node)  \
((node)->__rb_parent_color == (unsigned long)(node))
#define RB_CLEAR_NODE(node)  \
((node)->__rb_parent_color = (unsigned long)(node))

// rb_black 低位为1，rb_red 低位为0
#define __rb_color(pc)     ((pc) & 1)
#define __rb_is_black(pc)  __rb_color(pc)
#define __rb_is_red(pc)    (!__rb_color(pc))
// 获取结点的颜色
#define rb_color(rb)       __rb_color((rb)->__rb_parent_color)
// 判断结点的颜色是否是红色
#define rb_is_red(rb)      __rb_is_red((rb)->__rb_parent_color)
// 判断结点的颜色是否是黑色
#define rb_is_black(rb)    __rb_is_black((rb)->__rb_parent_color)

// 设置结点为黑色
static inline void rb_set_black(struct rb_node *rb)
{
rb->__rb_parent_color |= RB_BLACK;
}
// 获取结点的父结点
static inline struct rb_node *rb_red_parent(struct rb_node *red)
{
return (struct rb_node *)red->__rb_parent_color;
}
// 设置结点的父结点
static inline void rb_set_parent(struct rb_node *rb, struct rb_node *p)
{
rb->__rb_parent_color = rb_color(rb) | (unsigned long)p;
}
// 设置父结点+自身颜色信息
static inline void rb_set_parent_color(struct rb_node *rb,
       struct rb_node *p, int color)
{
rb->__rb_parent_color = (unsigned long)p | color;
}

3.3 插入结点

插入结点的情况分为多种，这里先做一些前提说明：

augment_rotate 树旋转时可以进行的额外操作。

G为祖先结点，P为父结点，U为父结点的兄弟结点，n为当前结点。

新插入的结点默认为红色的，如果父结点为黑色，则没有违背红黑树的性质。如果双亲结点为红色，则违背了性质，针对不同情况进行分析。

情况一：P和U均为红色，当前插入的结点n为P的左结点。而这里的G肯定是为黑色，如果为红色，在插入之前就已经违反了性质的要求。这次插入只需要进行颜色的修改，因为P和其兄弟结点存在不同的路径上且均为红色，只需要同时改为黑色，就不会影响性质④，但是这时候会影响性质③，所以只需要将父结点改为红色即可。
情况二：P为红色，n为红色且在P的左结点。U可能不存在或者为黑色结点，G为黑色。这种情况下，需要再细分成两种情况来讨论，就是U结点存在或者不存在。若是P结点为G结点的左孩子，n结点为P结点的左孩子，进行右单旋。若是P结点为G结点的右孩子，n为P结点的右孩子，则进行左单旋。
- U结点不存在，那么n一定是新插入的结点，n和P为红色，不满足性质③。
- U结点存在且为黑色，那么n结点在修改之前一定是黑色的。如果不是黑色的，就不满足性质④。
情况三：n为红色，P为红色，G为黑色，U可能不存在或者为黑色结点。与情况二不同的是，若P结点为G的左孩子，那么n结点为P结点的右孩子，则进行左单旋。若P结点为G的右孩子，那么n结点为P结点的左孩子，则进行右单旋。

static __always_inline void
__rb_insert(struct rb_node *node, struct rb_root *root,
    void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
struct rb_node *parent = rb_red_parent(node), *gparent, *tmp;

while (true) {
/*
 * Loop invariant: node is red
 *
 * If there is a black parent, we are done.
 * Otherwise, take some corrective action as we don't
 * want a red root or two consecutive red nodes.
 */
// 如果parent为空，表示当前的结点为根结点，根结点为黑色
// 如果父结点为黑色，直接返回
if (!parent) {
rb_set_parent_color(node, NULL, RB_BLACK);
break;
} else if (rb_is_black(parent))
break;

// 拿到祖先结点
gparent = rb_red_parent(parent);

tmp = gparent->rb_right;
if (parent != tmp) {/* parent == gparent->rb_left */
if (tmp && rb_is_red(tmp)) {
/*
 * Case 1 - color flips
 *
 *       G            g
 *      / \          / \
 *     p   u  -->   P   U
 *    /            /
 *   n            n
 *
 * However, since g's parent might be red, and
 * 4) does not allow this, we need to recurse
 * at g.
 */
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);
continue;
}

tmp = parent->rb_right;
if (node == tmp) {
/*
 * Case 2 - left rotate at parent
 *
 *      G             G
 *     / \           / \
 *    p   U  -->    n   U
 *     \           /
 *      n         p
 *
 * This still leaves us in violation of 4), the
 * continuation into Case 3 will fix that.
 */
parent->rb_right = tmp = node->rb_left;
node->rb_left = parent;
if (tmp)
rb_set_parent_color(tmp, parent,
    RB_BLACK);
rb_set_parent_color(parent, node, RB_RED);
augment_rotate(parent, node);
parent = node;
tmp = node->rb_right;
}

/*
 * Case 3 - right rotate at gparent
 *
 *        G           P
 *       / \         / \
 *      p   U  -->  n   g
 *     /                 \
 *    n                   U
 */
gparent->rb_left = tmp;  /* == parent->rb_right */
parent->rb_right = gparent;
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;
} else {
tmp = gparent->rb_left;
if (tmp && rb_is_red(tmp)) {
/* Case 1 - color flips */
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);
continue;
}

tmp = parent->rb_left;
if (node == tmp) {
/* Case 2 - right rotate at parent */
parent->rb_left = tmp = node->rb_right;
node->rb_right = parent;
if (tmp)
rb_set_parent_color(tmp, parent,
    RB_BLACK);
rb_set_parent_color(parent, node, RB_RED);
augment_rotate(parent, node);
parent = node;
tmp = node->rb_left;
}

/* Case 3 - left rotate at gparent */
gparent->rb_right = tmp;  /* == parent->rb_left */
parent->rb_left = gparent;
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;
}
}
}

static inline void
__rb_rotate_set_parents(struct rb_node *old, struct rb_node *new,
struct rb_root *root, int color)
{
struct rb_node *parent = rb_parent(old);
new->__rb_parent_color = old->__rb_parent_color;
rb_set_parent_color(old, new, color);
__rb_change_child(old, new, parent, root);
}

// dummy_rotate默认操作，实际内容为空
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
__rb_insert(node, root, dummy_rotate);
}

3.4 删除结点

红黑树的删除可能比较复杂，在阅读下面内容之前，我推荐两个地方：

《算法导论》或者《STL源码剖析》。
bilibili 红黑树-删除

下面分不同的情况来讨论(不包括空节点)：

没有孩子的红色节点，直接删除。
只有左孩子/右孩子，用孩子节点直接替代且变为黑色。这里为什么是只有左孩子和右孩子，而不是树的情况呢。因为我们要删除的节点G只能是黑色，而它的孩子节点P必然是红色，那P的孩子节点n无论是红色或者黑色均会违反性质，所以是不可能有孩子节点的。如果要删除的节点只有左边或者右边，那么只可能是节点而不是子树。那为什么删除的节点不可能是红色且只存在左孩子和右孩子的情况呢？是因为一旦它的孩子无论是黑色还是红色都会违反红黑树的性质。
没有孩子的黑色节点，我们会将当前要删除的节点先变成双黑节点。之后再分类将其变回单黑节点。
- 兄弟节点为黑色。
  - 兄弟节点至少有一个红色的孩子节点。根据类型细分为(LL,RR,LR,RL)型，根据这些类型进行变色+旋转。具体情况可以在这里查看不同类型的细分讨论。
  - 兄弟节点都是黑色的节点，将兄弟节点变成红色节点，并且让当前双黑节点变成其父节点是双黑节点。但是如果其分节点为红色的情况下，只需要变成单黑即可。然后将要删除的节点删掉之后，但是我们发现这里的双黑节点只是进行了转移，而并非真正的删除。那么我们以新的双黑节点来讨论是满足哪种情况。
- 兄弟节点为红色，只需要将s->color = !s->color; p->color = !p->color;，也就是兄弟节点以及其父节点变色。之后将p朝向双黑节点进行旋转。然后我们继续以双黑节点来讨论是满足哪种情况。
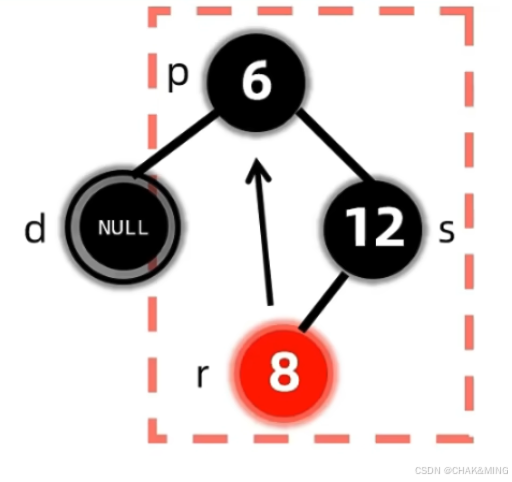
左右孩子都有，会先通过直接前驱或者直接后继的替换，然后将问题转移到被替换的结点。

下面根据类型细分不同情况：

LL型。这里的LL型指的是双黑节点的兄弟节点满足它是它的父节点的左子树和它的左孩子为红色节点。这里同样包含左右孩子都存在，且是红色的节点。那么我们先采取变色操作，r->color = s->color; s->color = p->color。然后对p节点进行右旋操作right_rotate(p)。然后将双黑节点变成单黑节点。

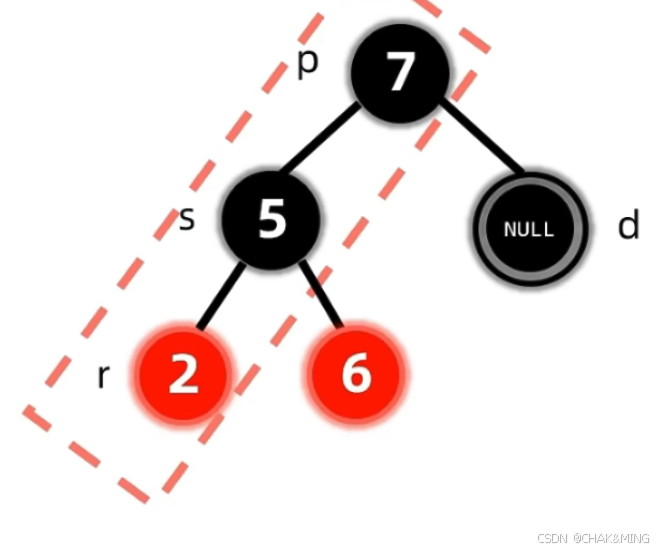
RR型。这里的操作与LL型类似。变色操作采取相同的策略，然后对p节点进行左旋操作left_rotate(p)，最后同样将双黑节点变成单黑节点。

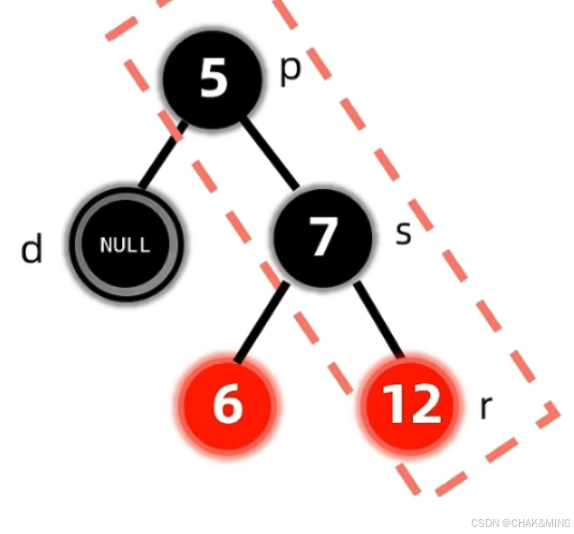
LR型。这里指的是双黑节点的兄弟节点s满足它的是父节点的左孩子和它的右孩子为红色节点。之后采取变色操作，先将r->color = p->color; p->color = RB_BLACK;，然后对left_rotate(s); right_rotate(p);，最后双黑节点变成单黑节点。

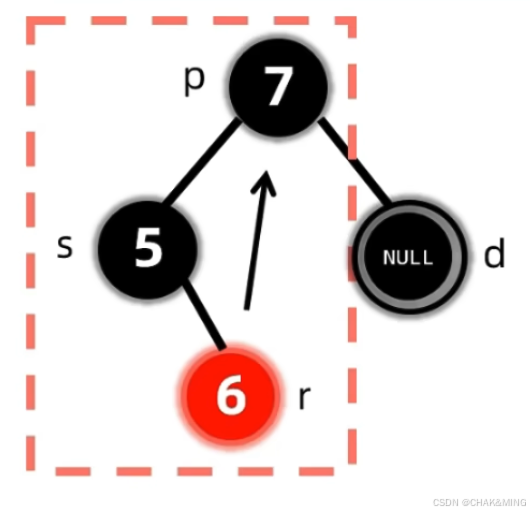
RL型。这里指的是双黑节点的兄弟节点s满足它的是父节点的右孩子和它的左孩子为红色节点。变色操作与LR型一致，然后对right_rotate(s); left_rotate(p);，最后双黑节点变成单黑节点。

上面讨论完红黑树删除的理论后，我们贴一下Linux内核中的实现。

/*
 * Inline version for rb_erase() use - we want to be able to inline
 * and eliminate the dummy_rotate callback there
 */
static __always_inline void
____rb_erase_color(struct rb_node *parent, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
struct rb_node *node = NULL, *sibling, *tmp1, *tmp2;

while (true) {
/*
 * Loop invariants:
 * - node is black (or NULL on first iteration)
 * - node is not the root (parent is not NULL)
 * - All leaf paths going through parent and node have a
 *   black node count that is 1 lower than other leaf paths.
 */
sibling = parent->rb_right;
if (node != sibling) {/* node == parent->rb_left */
if (rb_is_red(sibling)) {
/*
 * Case 1 - left rotate at parent
 *
 *     P               S
 *    / \             / \
 *   N   s    -->    p   Sr
 *      / \         / \
 *     Sl  Sr      N   Sl
 */
parent->rb_right = tmp1 = sibling->rb_left;
sibling->rb_left = parent;
rb_set_parent_color(tmp1, parent, RB_BLACK);
__rb_rotate_set_parents(parent, sibling, root,
RB_RED);
augment_rotate(parent, sibling);
sibling = tmp1;
}
tmp1 = sibling->rb_right;
if (!tmp1 || rb_is_black(tmp1)) {
tmp2 = sibling->rb_left;
if (!tmp2 || rb_is_black(tmp2)) {
/*
 * Case 2 - sibling color flip
 * (p could be either color here)
 *
 *    (p)           (p)
 *    / \           / \
 *   N   S    -->  N   s
 *      / \           / \
 *     Sl  Sr        Sl  Sr
 *
 * This leaves us violating 5) which
 * can be fixed by flipping p to black
 * if it was red, or by recursing at p.
 * p is red when coming from Case 1.
 */
rb_set_parent_color(sibling, parent,
    RB_RED);
if (rb_is_red(parent))
rb_set_black(parent);
else {
node = parent;
parent = rb_parent(node);
if (parent)
continue;
}
break;
}
/*
 * Case 3 - right rotate at sibling
 * (p could be either color here)
 *
 *   (p)           (p)
 *   / \           / \
 *  N   S    -->  N   Sl
 *     / \             \
 *    sl  Sr            s
 *                       \
 *                        Sr
 */
sibling->rb_left = tmp1 = tmp2->rb_right;
tmp2->rb_right = sibling;
parent->rb_right = tmp2;
if (tmp1)
rb_set_parent_color(tmp1, sibling,
    RB_BLACK);
augment_rotate(sibling, tmp2);
tmp1 = sibling;
sibling = tmp2;
}
/*
 * Case 4 - left rotate at parent + color flips
 * (p and sl could be either color here.
 *  After rotation, p becomes black, s acquires
 *  p's color, and sl keeps its color)
 *
 *      (p)             (s)
 *      / \             / \
 *     N   S     -->   P   Sr
 *        / \         / \
 *      (sl) sr      N  (sl)
 */
parent->rb_right = tmp2 = sibling->rb_left;
sibling->rb_left = parent;
rb_set_parent_color(tmp1, sibling, RB_BLACK);
if (tmp2)
rb_set_parent(tmp2, parent);
__rb_rotate_set_parents(parent, sibling, root,
RB_BLACK);
augment_rotate(parent, sibling);
break;
} else {
sibling = parent->rb_left;
if (rb_is_red(sibling)) {
/* Case 1 - right rotate at parent */
parent->rb_left = tmp1 = sibling->rb_right;
sibling->rb_right = parent;
rb_set_parent_color(tmp1, parent, RB_BLACK);
__rb_rotate_set_parents(parent, sibling, root,
RB_RED);
augment_rotate(parent, sibling);
sibling = tmp1;
}
tmp1 = sibling->rb_left;
if (!tmp1 || rb_is_black(tmp1)) {
tmp2 = sibling->rb_right;
if (!tmp2 || rb_is_black(tmp2)) {
/* Case 2 - sibling color flip */
rb_set_parent_color(sibling, parent,
    RB_RED);
if (rb_is_red(parent))
rb_set_black(parent);
else {
node = parent;
parent = rb_parent(node);
if (parent)
continue;
}
break;
}
/* Case 3 - right rotate at sibling */
sibling->rb_right = tmp1 = tmp2->rb_left;
tmp2->rb_left = sibling;
parent->rb_left = tmp2;
if (tmp1)
rb_set_parent_color(tmp1, sibling,
    RB_BLACK);
augment_rotate(sibling, tmp2);
tmp1 = sibling;
sibling = tmp2;
}
/* Case 4 - left rotate at parent + color flips */
parent->rb_left = tmp2 = sibling->rb_right;
sibling->rb_right = parent;
rb_set_parent_color(tmp1, sibling, RB_BLACK);
if (tmp2)
rb_set_parent(tmp2, parent);
__rb_rotate_set_parents(parent, sibling, root,
RB_BLACK);
augment_rotate(parent, sibling);
break;
}
}
}

/* Non-inline version for rb_erase_augmented() use */
void __rb_erase_color(struct rb_node *parent, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
____rb_erase_color(parent, root, augment_rotate);
}

3.5 遍历红黑树

Linux内核提供了四个函数，用于以排序的方式遍历一颗红黑树的内容。

// 返回红黑树排序后第一个节点，也就是最小的值的节点
struct rb_node *rb_first(struct rb_root *tree);
// 返回红黑树排序后最后一个节点，也就是最大的值的节点
struct rb_node *rb_last(struct rb_root *tree);
// 返回当前节点的下一个节点(后继)。
struct rb_node *rb_next(struct rb_node *node);
// 返回当前节点的前一个节点(前驱)。
struct rb_node *rb_prev(struct rb_node *node);

/*
 * 具体代码分析
 * 红黑树本质上是一种二叉搜索树，而二叉搜索树每个子树满足左 < 根 < 右
*/
// 最左子树的根节点为最小的值的节点
struct rb_node *rb_first(const struct rb_root *root)
{
struct rb_node*n;

n = root->rb_node;
if (!n)
return NULL;
while (n->rb_left)
n = n->rb_left;
return n;
}

// 最右子树的根节点为最大的值的节点
struct rb_node *rb_last(const struct rb_root *root)
{
struct rb_node*n;

n = root->rb_node;
if (!n)
return NULL;
while (n->rb_right)
n = n->rb_right;
return n;
}

struct rb_node *rb_next(const struct rb_node *node)
{
struct rb_node *parent;

    // 判断当前节点是不是空节点
if (RB_EMPTY_NODE(node))
return NULL;

// 如果当前节点的右节点存在，我们会获取它的最左子树的根节点
if (node->rb_right) {
node = node->rb_right; 
while (node->rb_left)
node=node->rb_left;
return (struct rb_node *)node;
}

// 如果不存在当前节点的右节点，先考虑当前的父节点，如果当前节点为父节点的右孩子的，则继续往下寻找
while ((parent = rb_parent(node)) && node == parent->rb_right)
node = parent;

return parent;
}

struct rb_node *rb_prev(const struct rb_node *node)
{
struct rb_node *parent;

if (RB_EMPTY_NODE(node))
return NULL;

// 如果当前节点的左节点存在，我们会获取它的最右子树的根节点
if (node->rb_left) {
node = node->rb_left; 
while (node->rb_right)
node=node->rb_right;
return (struct rb_node *)node;
}

// 如果不存在当前节点的左节点，先考虑当前的父节点，如果当前节点为父节点的左孩子的，则继续往下寻找
while ((parent = rb_parent(node)) && node == parent->rb_left)
node = parent;

return parent;
}

4. 案例演示

到此内核源码大致了解清楚后，我们尝试编写内核代码去使用它。

// 创建一个包含红黑树节点的结构体
struct test_node {
struct rb_node rb;
int key;

int val;
int augmented;
};

#define NODES10000
static struct rb_root root = RB_ROOT;
static struct test_node nodes[NODES];

// 插入结点
static void insert(struct test_node *node, struct rb_root *root)
{
struct rb_node **new = &(root->rb_node), *parent = NULL;

int key = node->key;

// 根据二叉搜索树的性质找到要插入的位置
while(*new) {
parent = *new;
        // rb_entry是获取parent结点所在的test_node结构体的数据
if (key < rb_entry(parent, struct test_node, rb)->key)
new = &parent->rb_left;
else
new = &parent->rb_right;
}

    // 把parent设置为node的父节点，并且让new指向&node->rb
rb_link_node(&node->rb, parent, new);
    // 将该节点插入
rb_insert_color(&node->rb, root);
}

// 删除节点
void erase(struct test_node *node, struct rb_root *root)
{
    rb_erase(&node->rb, root);
}

static int black_path_count(struct rb_node *rb) {
int count;
for (count = 0; rb; rb = rb_parent(rb))
count += !rb_is_red(rb);

return count;
}

// 检查红黑树的有效性
static void check(int nr_nodes)
{
struct rb_node *rb;
int count = 0, blacks = 0;
int prev_key = 0;

for (rb = rb_first(&root); rb; rb=rb_next(rb)) {
struct test_node *node = rb_entry(rb, struct test_node, rb);
        // 节点是否按照升序排序
if (node->key < prev_key)
printf("[WARN] node->key(%d) < prev_key(%d)\n", node->key, prev_key);
        // 没有两个连续的红色节点
if (rb_is_red(rb) && (!rb_parent(rb) || rb_is_red(rb_parent(rb))))
printf("[WARN] two red nodes\n");
        // 根节点到所有叶子节点的路径中，黑色节点的数量是一致的。
if (!count)
blacks = black_path_count(rb);
else if ((!rb->rb_left || !rb->rb_right) && (blacks != black_path_count(rb)))
printf("[WARN] black count wrongs\n");

prev_key = node->key;
count++;
}
}

// 打印红黑树的节点
void print_rbtree(struct rb_root *tree)
{
struct rb_node *node;

for (node = rb_first(tree); node; node = rb_next(node))
printf("%d ", rb_entry(node, struct test_node, rb)->key);
printf("\n");
}

// 搜索红黑树是否有节点的值为num
int search_rbtree(struct rb_root *tree, int num){
struct rb_node *node;

for (node = rb_first(tree); node; node = rb_next(node)) {
if (num == rb_entry(node, struct test_node, rb)->key)
return true;
}

return false;
}

static void safe_flush()
{
    char c;

    while((c = getchar()) != '\n' && c != EOF);
}

int main(int argc, char *argv[])
{
int i, j;
int num;

srand(time(NULL));
for (i = 0; i < NODES; i++) {
nodes[i].key = i;
nodes[i].val = i;
}

/* insert */
for(j = 0; j < NODES; j++) {
insert(nodes + j, &root);
}

/* check */
check(0);

        /* print_rbtree(&root); */
while(1) {
num = -2;
printf("Please input the num which you want to search in rbtree.\n");
printf("The input num should be 0 <= input num < 10000\n");
printf("Input -1 to exit\n");
printf(">>> ");

scanf("%d", &num);

if (num == -1)
goto exit;

if (num < 0 || num > 10000) {
printf("WARNNING: Invalild input number!\n");
safe_flush();
continue;
}

if (search_rbtree(&root, num))
printf("RESULT: Found %d in the rbtree\n", num);
else
printf("RESULT: Not Found %d in the rbtree\n", num);

}
exit:
/* erase */
for(j = 0; j < NODES; j++) {
erase(nodes + j, &root);
}

return 0;
}

5. 拓展

增强红黑树的支持，暂未编写。

原文地址：https://blog.csdn.net/CHAKMING1/article/details/140617118

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

上一篇：恶趣味猜数字+关机（C语言游戏）
下一篇：Kafka之存储设计

医学数据分析实训项目十基于深度残差神经网络的皮肤癌检测
皮肤镜图像是检查皮肤癌黑色素瘤的主要手段。本实践项目通过构建深度残差神经网络提取皮肤镜图像的高维特征，使用残差学习防止网络梯度退化，降低网络训练的难度，实现黑色素瘤的有效识别。实践项目所使用的数据集由
阅读更多2024-09-20
提升工作效率，引领编程新时代
&emsp;&emsp;&emsp;&emsp;---
阅读更多2024-09-20
滑动窗口(7)_串联所有单词的字串
滑动窗口(7)_串联所有单词的字串,困难级别题目?思路对照样秒AC!!!
阅读更多2024-09-20
Redis性能测试redis-benchmark
你可以获取 Redis 的性能数据，帮助优化配置和硬件资源。如果有特定的场景或命令需要测试，可以详细说明，我可以提供更具体的建议！会输出每个命令的吞吐量（请求每秒）和其他性能指标。这些指标可以帮助你了
阅读更多2024-09-20
ChartLlama: A Multimodal LLM for Chart Understanding and Generation论文阅读
多模态大型语言模型在大多数视觉语言任务中表现出令人印象深刻的表现。但是，该模型通常缺乏对特定域数据的理解能力，尤其是在解释图表图片时。这主要是由于缺乏相关的多模态指令微调数据集。在本文中，我们利用 G
阅读更多2024-09-20
react hooks--useMemo
相当于计算属性!!!useMemo实际的目的也是为了进行性能的优化。◼ 如何进行性能的优化呢？ useMemo返回的也是一个 memoized（记忆的）值； 在依赖不变的情况下，多次定义的时候，
阅读更多2024-09-20
zookeeper向管控平台上报状态
report_status_to_zookeeper() 方法二：第一个 worker 进程上报如果你希望使用第一个工作进程来上报状态，而不是主进程，可以使用进程 ID 来判断： import os
阅读更多2024-09-20
深蓝学院-- 量产自动驾驶中的规划控制算法小鹏
来源：深蓝学院：《量产自动驾驶中的规划控制算法》
阅读更多2024-09-20
加密与安全_三种常见的注入攻击
注入攻击是指攻击者通过传递恶意数据，将这些数据当作代码在目标系统中执行。这类攻击的本质是数据与代码的边界被打破，导致数据被误执行。SQL注入（SQL Injection）：攻击者通过恶意构造的SQL语
阅读更多2024-09-20
Prompt最佳实践｜如何用参考文本让ChatGPT答案更精准？
想象一下，你正在参加一个烹饪比赛，而你的目标是制作出世界上最美味的蛋糕。尽管你对烹饪充满热情，你却不知道那个秘密配方。这时，组织者给了你一个选择：使用一本包含世界顶级糕点师秘密配方的烹饪书。这本书正是
阅读更多2024-09-20

Linux 红黑树内核源码剖析