C++ AVL树详细讲解

template<class T>
struct AVLTreeNode
{
AVLTreeNode(const T& data)
: _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
, _data(data), _bf(0)
{}
AVLTreeNode<T>* _pLeft;   // 该节点的左孩子
AVLTreeNode<T>* _pRight;  // 该节点的右孩子
AVLTreeNode<T>* _pParent; // 该节点的双亲
T _data;
int _bf;                  // 该节点的平衡因子
};

2.AVL树的插入

AVL 树就是在二叉搜索树的基础上引入了平衡因子，因此 AVL 树也可以看成是二叉搜索树。那么

AVL 树的插入过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点

2. 调整节点的平衡因子

bool Insert(const pair<K, V>& kv)
{
    // 1. 先按照二叉搜索树的规则将节点插入到AVL树中

if (_root == nullptr)
{
_root = new Node(kv);
return true;
}

Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
//插入相同值
return false;
}
}

//找到cur所在位置
cur = new Node(kv);
if (parent->_kv.first > cur->_kv.first)
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}

     // 2. 新节点插入后，AVL树的平衡性可能会遭到破坏，此时就需要更新平衡因子，并检测是否
    //破坏了AVL树的平衡性
    
     /*
     pCur插入后，pParent的平衡因子一定需要调整，在插入之前，pParent
     的平衡因子分为三种情况：-1，0, 1, 分以下两种情况：
      1. 如果pCur插入到pParent的左侧，只需给pParent的平衡因子-1即可
      2. 如果pCur插入到pParent的右侧，只需给pParent的平衡因子+1即可
  
     此时：pParent的平衡因子可能有三种情况：0，正负1， 正负2
      1. 如果pParent的平衡因子为0，说明插入之前pParent的平衡因子为正负1，插入后被调整成0，此时满足
AVL树的性质，插入成功
      2. 如果pParent的平衡因子为正负1，说明插入前pParent的平衡因子一定为0，插入后被更新成正负1，此
时以pParent为根的树的高度增加，需要继续向上更新
      3. 如果pParent的平衡因子为正负2，则pParent的平衡因子违反平衡树的性质，需要对其进行旋转处理
     */

    //更新平衡因子
while (parent)
{
if (parent->_left == cur)
{
parent->_bf--;
}
else
{
parent->_bf++;
}

if (parent->_bf == 0)
{
//二叉树高度没问题，更新结束
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
            // 插入前双亲的平衡因子是0，插入后双亲的平衡因子为1 或者 -1 ，说明以双亲为根的二叉树
            // 的高度增加了一层，因此需要继续向上调整
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == -2 || parent->_bf == 2)
{
            //双亲的平衡因子为正负2，违反了AVL树的平衡性
//二叉树平衡被破坏，需要旋转完成平衡
//判断是右单旋还是左单旋还是双旋

//右单旋
if (parent->_bf == -2 && cur->_bf == -1)
{
//...
}
//左单旋
else if (parent->_bf == 2 && cur->_bf == 1)
{
//...
}
//左右双旋
else if (parent->_bf == -2 && cur->_bf == 1)
{
                //...
}
//右左双旋
else if (parent->_bf == 2 && cur->_bf == -1)
{
                //...
}

}
else
{
//理论上不会出现这种状况
assert(false);
}
}

return true;
}

3.AVL树的旋转

如果在一棵原本是平衡的 AVL 树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，

使之平衡化。根据节点插入位置的不同， AVL 树的旋转分为四种：

1) 新节点插入较高左子树的左侧---左左：右单旋

/*
  上图在插入前，AVL树是平衡的，新节点插入到30的左子树(注意：此处不是左孩子)中，30左
子树增加
  了一层，导致以60为根的二叉树不平衡，要让60平衡，只能将60左子树的高度减少一层，右子
树增加一层，
  即将左子树往上提，这样60转下来，因为60比30大，只能将其放在30的右子树，而如果30有
右子树，右子树根的值一定大于30，小于60，只能将其放在60的左子树，旋转完成后，更新节点
的平衡因子即可。在旋转过程中，有以下几种情况需要考虑：
  1. 30节点的右孩子可能存在，也可能不存在
  2. 60可能是根节点，也可能是子树
     如果是根节点，旋转完成后，要更新根节点
     如果是子树，可能是某个节点的左子树，也可能是右子树
    
此处可举一些详细的例子进行画图，考虑各种情况，加深旋转的理解
*/
void _RotateR(Node Parent)
{
// SubL: Parent的左孩子
// SubLR: Parent左孩子的右孩子，注意：该
Node SubL = Parent->_Left;
Node SubLR = SubL->_Right;
// 旋转完成之后，30的右孩子作为双亲的左孩子
Parent->_Left = SubLR;
// 如果30的左孩子的右孩子存在，更新亲双亲
if (SubLR)
SubLR->_Parent = Parent;
// 60 作为 30的右孩子
SubL->_Right = Parent;

// 因为60可能是棵子树，因此在更新其双亲前必须先保存60的双亲
Node Parent = Parent->_Parent;

// 更新60的双亲
Parent->_Parent = SubL;

// 更新30的双亲
SubL->_Parent = Parent;
// 如果60是根节点，根新指向根节点的指针
if (NULL == Parent)
{
_root = SubL;
SubL->_Parent = NULL;
}
else
{
// 如果60是子树，可能是其双亲的左子树，也可能是右子树
if (Parent->_Left == Parent)
Parent->_Left = SubL;
else
Parent->_Right = SubL;
}
// 根据调整后的结构更新部分节点的平衡因子
Parent->_bf = SubL->_bf = 0;
}

2) 新节点插入较高右子树的右侧---右右：左单旋

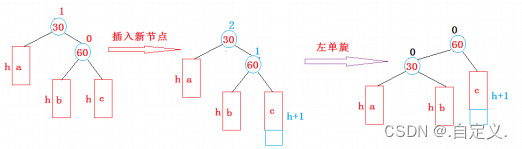
//左单旋
void LNode(Node* parent)
{
/*if (parent == _root)
{
Node* pparent = nullptr;
}
else
{
Node* pparent = parent->_parent;
}*/
Node* pparent = parent->_parent;

Node* subR = parent->_right;
Node* subRL = subR->_left;

parent->_left = subRL;
if (subRL)
subRL->_parent = parent;

subR->_left = parent;
parent->_parent = subR;

if (pparent)
{
subR->_parent = pparent;

if (pparent->_left = parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;
}
}
else
{
_root = subR;
subR->_parent = nullptr;
}

parent->_bf = subR->_bf = 0;
}

3) 新节点插入较高左子树的右侧---左右：先左单旋再右单旋

将双旋变成单旋后再旋转，即：先对 30 进行左单旋，然后再对 90 进行右单旋 ，旋转完成后再

考虑平衡因子的更新。

// 旋转之前，60的平衡因子可能是-1/0/1，旋转完成之后，根据情况对其他节点的平衡因子进
//行调整
void _RotateLR(Node Parent)
{
Node SubL = Parent->_Left;
Node SubLR = SubL->_Right;

// 旋转之前，保存pSubLR的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节
点的平衡因子
int bf = SubLR->_bf;

// 先对30进行左单旋
_RotateL(Parent->_Left);

// 再对90进行右单旋
_RotateR(Parent);
if (1 == bf)
SubL->_bf = -1;
else if (-1 == bf)
Parent->_bf = 1;
}

4) 新节点插入较高右子树的左侧---右左：先右单旋再左单旋

//右左双旋
void RLNode(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;

int bf = subRL->_bf;

RNode(parent->_right);
LNode(parent);

if (bf == 1)
{
subRL->_bf = 0;
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subRL->_bf = 0;
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf == 0)
{
subRL->_bf = 0;
subR->_bf = 0;
parent->_bf = 0;
}
else
{
//理论没有该状况
assert(false);
}
}

总结：

假如以 Parent 为根的子树不平衡，即 Parent 的平衡因子为 2 或者 -2 ，分以下情况考虑

1）Parent 的平衡因子为 2 ，说明 Parent 的右子树高，设 Parent 的右子树的根为 SubR

当 SubR 的平衡因子为 1 时，执行左单旋

当 SubR 的平衡因子为 -1 时，执行右左双旋

2）Parent 的平衡因子为 -2 ，说明 Parent 的左子树高，设 Parent 的左子树的根为 SubL

当 SubL 的平衡因子为 -1 是，执行右单旋

当 SubL 的平衡因子为 1 时，执行左右双旋

旋转完成后，原 Parent 为根的子树个高度降低，已经平衡，不需要再向上更新。

4.AVL树的验证

AVL 树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证 AVL 树，可以分两步：

1. 验证其为二叉搜索树

如果中序遍历可得到一个有序的序列，就说明为二叉搜索树

2. 验证其为平衡树

● 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子 )

● 节点的平衡因子是否计算正确

int _size(Node* root)
{
return root == nullptr ? 0 : _size(root->_left) + _size(root->_right) + 1；
}

int _Height(Node* root)
{
if (root == nullptr)
{
return 0;
}

return max(_Height(root->_left), _Height(root->_right)) + 1;
}

bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}

int LeftHeight = _Height(root->_left);
int RightHeight = _Height(root->_right);

if (abs(LeftHeight - RightHeight) >= 2)
{
return false;
}

//可以顺便再检查一下平衡因子
if (abs(LeftHeight - RightHeight) != root->_bf)
{
cout << root->_kv.first << endl;
return false;
}

return _IsBalance(root->_left) && _IsBalance(root->_right);
}

三、AVL树的性能

AVL 树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过 1 ，这

样可以保证查询时高效的时间复杂度，即 log2 N 。但是如果要对 AVL 树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的 ( 即不会改变 ) ，可以考虑 AVL 树，但一个结构经常修改，就不太适合。

四、完结撒❀

如果以上内容对你有帮助不妨点赞支持一下，以后还会分享更多编程知识，我们一起进步。
最后我想讲的是，据说点赞的都能找到漂亮女朋友❤

原文地址：https://blog.csdn.net/foodsx/article/details/139520890

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

上一篇：【C++初阶学习】第十二弹——stack和queue的介绍和使用
下一篇：【C/C++基础实战】：用C++实现通讯录管理系统——含完整源码

leetcode289:生命游戏
根据，简称为，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。给定一个包含m × n个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态：1即为（live），或0即为
阅读更多2024-10-20
MongoDB数据恢复
注意：两个MongoDB的版本要一致，本文使用的是mongo:4.2.24。先把K8S上面的MongoDB 容器停止（可以把副本改成0）。1、将容器挂载MongoDB的数据目录备份到本地。经常是数据文
阅读更多2024-10-20
C#中实现事务
C#中实现事务
阅读更多2024-10-20
【LeetCode每日一题】——560.和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的子数组的个数。子数组是数组中元素的连续非空序列。
阅读更多2024-10-20
「漏洞复现」满客宝智慧食堂系统 selectUserByOrgId 未授权访问漏洞
请勿利用文章内的相关技术从事非法测试，由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失，均由使用者本人负责，作者不为此承担任何责任。工具来自网络，安全性自测，如有侵权请联系删除。本次
阅读更多2024-10-20
React面试题目（从基本到高级）
React前端面试常见题目涵盖了React的基础概念、组件、状态管理、生命周期、性能优化等多个方面。
阅读更多2024-10-20
12.个人博客系统（Java项目基于spring和vue）
1 在校学习的学生，可用于日常学习使用或是毕业设计使用 2 毕业一到两年的开发人员，用于锻炼自己的独立功能模块设计能力，增强代码编写能力。 3 亦可以部署为商化项目使用。 4 需要完整资料及源码
阅读更多2024-10-20
YoloV8改进策略：注意力改进|DeBiFormer，可变形双级路由注意力|引入DeBiLevelRoutingAttention注意力模块（全网首发）
本次改进的核心在于将DeBiLevelRoutingAttention模块嵌入到YoloV8的主干网络中，具体位置是在SPPF（Spatial Pyramid Pooling Fast）模块之后。这一
阅读更多2024-10-20
word取消自动单词首字母大写
情况说明：在word输入单词后首字母会自动变成大写取消单词首字母大写步骤：（1）点击菜单栏文件（2）点击“更多”——>“选项”（3）点击“校对”——>“自动更正选项”（4）取消“句首字母大
阅读更多2024-10-20
web前端网页用户注册页面
【代码】web前端网页用户注册页面。
阅读更多2024-10-20

C++ AVL树 详细讲解

一、AVL树的概念

二、AVL树的实现

1.AVL树节点的定义