数据结构 - C/C++ - 树

🕗 发布于 2024-07-07 20:17 数据结构 c语言 c++

公开视频 -> 链接点击跳转公开课程
博客首页 -> 链接点击跳转博客主页

树的概念

结构特性

树的概念

二叉树是树形结构，是一种非线性结构。
- 非线性结构：在二叉树中，数据项的排列不是简单的线性序列，而是通过节点间的链接构成复杂的层次结构。
- 受限节点数目：每个节点最多有两个子节点，这限定了树的分支宽度。
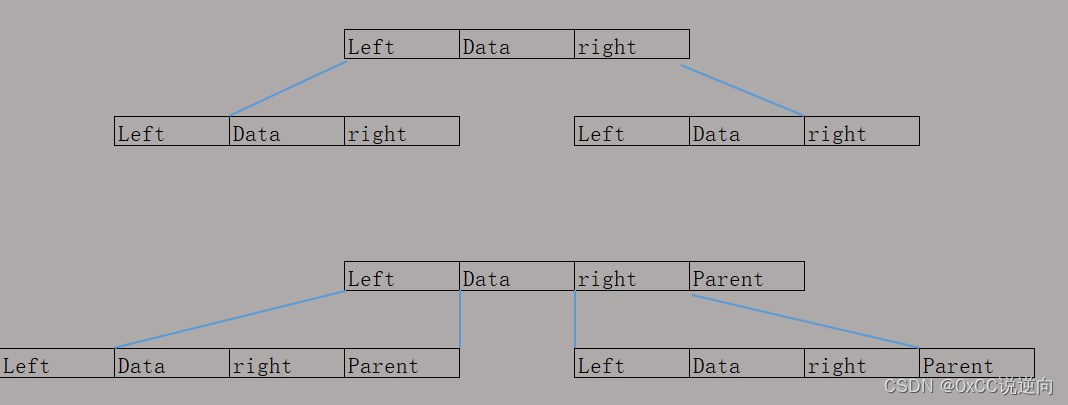
节点(Node)
- 数据域：保存或显示与节点相关联的信息。
- 左子节点指针：指向左侧子节点的链接。
- 右子节点指针：指向右侧子节点的链接。
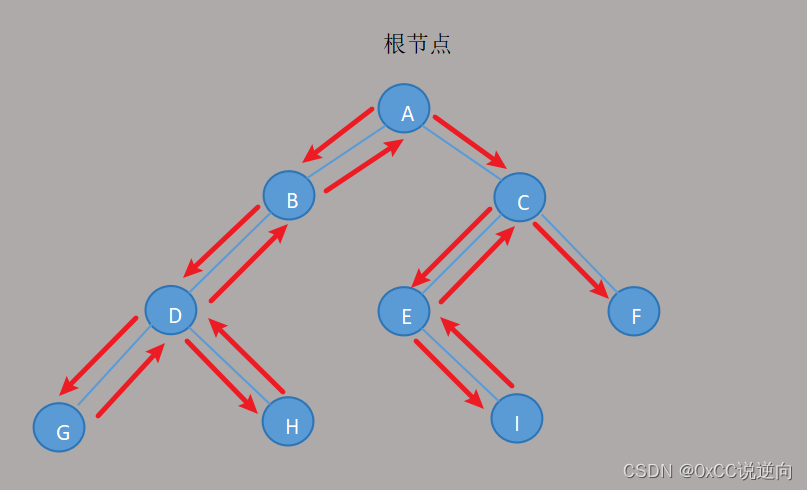
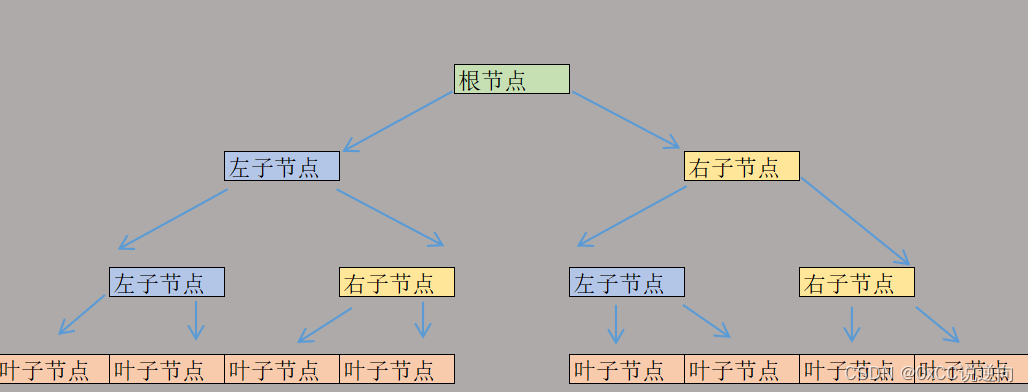
根节点(Root)
- 节点是树结构的最顶端节点，它没有父节点，并且是二叉树结构的起点。
父节点(Parent)
- 与子节点相关联的上一级节点。
子节点(Child)
- 父节点指向的左子节点或者右子节点。
叶子节点(Leaf)
- 叶子节点是指没有任何子节点的节点。在树的结构中，叶子节点总是位于最底层。
兄弟节点(Brother)
- 在二叉树中，共享同一父节点的两个节点称为兄弟节点。
节点的度
- 节点分支数。
- 度为0：节点没有子节点，即叶子节点。
- 度为1：节点有一个子节点。
- 度为2：节点有两个子节点。
结点层度：根节点的层次为1，以此递增。
树的深度：树种节点层次的最大值。

结构特性

二叉树中第I层中最多存在2^(I - 1)的节点数量。
二叉树中深度为I时最多存在2^I - 1的节点总数。

树的样式

二叉树
完美二叉树
- 完美二叉树中，除了叶子节点外其余所有节点的度都有2。
- 完美二叉树中，深度为I时节点数量为2^I - 1。

树的存储

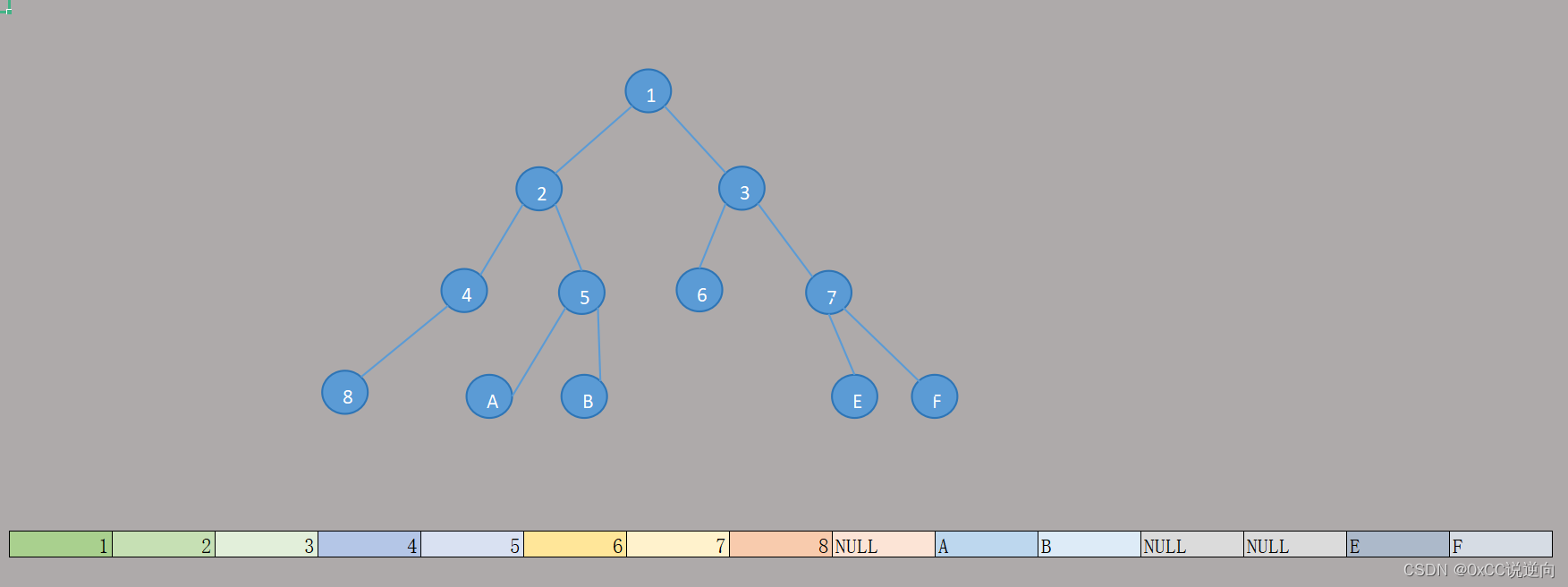
顺序存储
- 基于数组 - 内存中使用连续的内存空间
- 假设根节点编号为x
  - 左子节点编号为2 * x
  - 右子节点编号为2 * x + 1
链式存储
- 基于链表 - ListNode

树的遍历

先序遍历 DLR 根节点左子树右子树
中序遍历 LDR 左子树根节点右子树

后序遍历 LRD 左子树右子树根节点

示例代码

#include <iostream>

class TreeNode
{
public:
    char ch;
    TreeNode* Left;
    TreeNode* Righ;
    TreeNode(char value) : ch(value), Left(nullptr), Righ(nullptr) {}
};

void PreorderTraverse(TreeNode* T)
{
    if (T == NULL) return;
    printf("%c ", T->ch);
    PreorderTraverse(T->Left);
    PreorderTraverse(T->Righ);
}

void InOrderTraverse(TreeNode* T)
{
    if (T == NULL) return;
    InOrderTraverse(T->Left);
    printf("%c ", T->ch);
    InOrderTraverse(T->Righ);
}

void PostOrderTraverse(TreeNode* T)
{
    if (T == NULL) return;
    PostOrderTraverse(T->Left);
    PostOrderTraverse(T->Righ);
    printf("%c ", T->ch);
}

int main()
{
    //二叉树节点
#if 1
    TreeNode* NodeA = new TreeNode('A');
    TreeNode* NodeB = new TreeNode('B');
    TreeNode* NodeC = new TreeNode('C');
    TreeNode* NodeD = new TreeNode('D');
    TreeNode* NodeE = new TreeNode('E');
    TreeNode* NodeF = new TreeNode('F');
    TreeNode* NodeG = new TreeNode('G');
    TreeNode* NodeH = new TreeNode('H');
    TreeNode* NodeI = new TreeNode('I');
#endif

    //二叉树图解
    /*
                    A
                   / \
                  B   C
                 /   / \
                D   E   F
               / \   \
              G   H   I
    */

    //二叉树关联
#if 1
    NodeA->Left = NodeB;
    NodeB->Left = NodeD;
    NodeD->Left = NodeG;
    NodeD->Righ = NodeH;

    NodeA->Righ = NodeC;
    NodeC->Left = NodeE;
    NodeE->Righ = NodeI;
    NodeC->Righ = NodeF;
#endif

    //二叉树遍历
#if 1
    PreorderTraverse(NodeA);
    InOrderTraverse(NodeA);
    PostOrderTraverse(NodeA);
#endif

    return 0;
}

节点增删

假如删除节点为叶子节点，直接删除节点并修正父节点对应指向为NULL。
假如删除节点存在一个子节点，子节点替换被删除节点位置，并对应指向。
假如删除节点存在两个子节点。

    //二叉树节点
    TreeNode* InsertNode = new TreeNode('J');
    TreeNode* TempNode = NodeA->Left;

    NodeA->Left = InsertNode;
    InsertNode->Left = TempNode;

二叉搜索树

元素关联
- 根节点的左子树不为空，则左子树上的所有节点的值均小于它根节点的值。
- 根节点的右子树不为空，则右子树上的所有节点的值均大于它根节点的值。
- 根节点的左子树以及右子树均为二叉排序树。
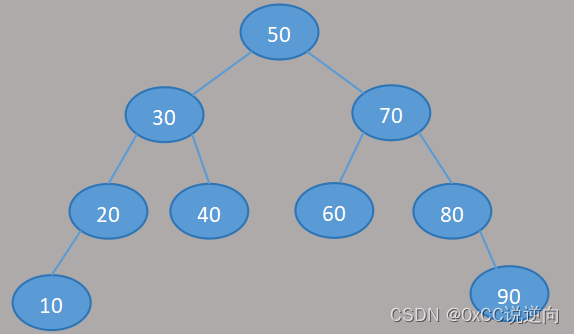
元素排列
- 中序遍历 LDR 左子树根节点右子树
- 10 20 30 40 50 60 70 80 90
元素搜索
- 通过根节点按左子节点遍历下去为最小值节点。
- 通过根节点按右子节点遍历下去为最大值节点。
- 查找指定节点二分(左小右大)。

删除节点

删除节点为叶子节点 - 直接删除节点，不会对当前结构产生影响。
删除节点仅存在左子树 - 删除节点左子树替换。
删除节点仅存在右子树 - 删除节点右子树替换。
删除节点同时存在左子树以及右子树 - 删除节点左子树内容挂在删除节点右子树中的左子节点，删除节点的右子节点替换被删除节点。
示例代码

#include <iostream>

class TreeNode
{
public:
    int value;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int Num) : value(Num), left(nullptr), right(nullptr){}
};

class BinarySearchTree
{
public:

    //插入节点
    TreeNode* Insert(TreeNode* Node, int value)
    {
        //50, 30, 20, 40, 70, 60, 80, 10, 90

        //空节点
        if (Node == NULL) return new TreeNode(value);

        //判断大小
        if (value < Node->value)
        {
            Node->left = Insert(Node->left, value);
        }
        else
        {
            Node->right = Insert(Node->right, value);
        }

        return Node;
    }

    //中序遍历
    void InOrderTraverse(TreeNode* Root)
    {
        if (Root == NULL) return;
        InOrderTraverse(Root->left);
        std::cout << Root->value << std::endl;
        InOrderTraverse(Root->right);
    }

    //查找节点
    TreeNode* Search(TreeNode* Node, int value)
    {
        if (Node == NULL) return NULL;
        if (Node->value == value) return Node;

        if (value < Node->value)
        {
            return Search(Node->left, value);
        }
        else
        {
            return Search(Node->right, value);
        }

    }

    //删除节点
    TreeNode* Delete(TreeNode* Root, int value)
    {
        if (Root == NULL) return NULL;

        //删除节点
        if (Root->value == value)
        {
            if (Root->left == NULL && Root->right == NULL)
            {
                delete Root;
                return NULL;
            }
            else if (Root->right == NULL && Root->left != NULL)
            {
                TreeNode* retNode = Root->left;
                delete Root;
                return retNode;
            }
            else if (Root->right != NULL && Root->left == NULL)
            {
                TreeNode* retNode = Root->right;
                delete Root;
                return retNode;
            }
            else
            {
                TreeNode* lastLeft = Root->right;
                while (lastLeft->left != NULL) lastLeft = lastLeft->left;
                lastLeft->left = Root->left;
                TreeNode* deleteNode = Root;
                Root = Root->right;
                delete deleteNode;
                return Root;
            }

        }

        if (Root->value > value)
        {
            Root->left = Delete(Root->left, value);
        }

        if (Root->value < value)
        {
            Root->right = Delete(Root->right, value);
        }

        return NULL;
    }
};

int main()
{
    BinarySearchTree BST;
    TreeNode* Root = NULL;

    int Arr[] = {30, 20, 40, 35,70, 60, 80, 10, 90 };

    Root = BST.Insert(Root, 50);
    for (size_t i = 0; i < sizeof(Arr) / sizeof(Arr[0]); i++)
    {
        BST.Insert(Root, Arr[i]);
    }

    BST.InOrderTraverse(Root);

    TreeNode* Temp = BST.Search(Root, 35);
    BST.Delete(Root, 70);

    return 0;
}

平衡二叉树

平衡二叉树
- 二叉排序树。
- 任何一个节点的左子树以及右子树都是平衡二叉树。
- 任何一个节点的左子树与右子树的高度差值的绝对值不能大于一。
平衡因子
- 节点的平衡因子为其节点左子树的高度减去其右子树的高度(0/1/-1)。
最小不平衡子树
- 二叉树中插入节点时，距离插入节点位置最近的BF值大于一的节点作为最小不平衡子树。
节点失衡
- 二叉树插入节点时，出现平衡因子绝对值大于一的最小不平衡子树。
- 通过“旋转”来修正最小不平衡子树。
旋转方式
- 左旋
  - 失衡节点的右子节点作为新的根节点。
  - 将失衡节点作为新的根节点的左子节点。
  - 新根节点如果存在左子树则转到旧根节点右子树下。
- 右旋
  - 失衡节点的左子节点作为新的根节点。
  - 将失衡节点作为新的根节点的右子节点。
  - 新根节点如果存在右子树则转到旧根节点左子树下。
- 旋转类型
  - LL(单右旋转)
    - 触发 - 插入节点发生在左子树的左侧
    - 操作 - 失衡节点的左子节点作为新的根节点，将失衡节点作为新的根节点的右子节点。
    - 图解
```
       3          2
      /          / \
     2          1   3
    / 
   1    
```
```
  - RR(单左旋转)

    - 触发 - 插入节点发生在右子树的右侧

    - 操作 - 失衡节点的右子节点作为新的根节点，将失衡节点作为新的根节点的左子节点。

    - 图解

      ```Objective-C++
      
                  3              6
                   \            / \
                    6          3   8
                   / \         \
                  5   8         5
```

模拟旋转

30 20 10 40 50 60 70 100 90

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>

//节点结构
typedef struct _Node
{
    int value;
    int height;
    struct _Node* left;
    struct _Node* right;
}Node;

//节点高度
int GetNodeHeight(Node* node)
{
    if (node == NULL) return NULL;
    return node->height;
}

//平衡因子
int GetNodeBalanceFactor(Node* node)
{
    if (node == NULL) return NULL;
    return GetNodeHeight(node->left) - GetNodeHeight(node->right);
}

//左旋处理
Node* LeftRotate(Node* node)
{
    //失衡节点的右子节点作为新的根节点
    Node* Root = node->right;
    Node* Temp = Root->left;

    //将失衡节点作为新的根节点的左子节点
    Root->left = node;

    //新根节点如果存在左子树则转到旧根节点右子树下
    node->right = Temp;

    //修正节点高度
    node->height = max(GetNodeHeight(node->left), GetNodeHeight(node->right)) + 1;
    Root->height = max(GetNodeHeight(Root->left), GetNodeHeight(Root->right)) + 1;

    return Root;
}

//右旋处理
Node* RightRotate(Node* node)
{
    //失衡节点的左子节点作为新的根节点
    Node* Root = node->left;
    Node* Temp = Root->right;

    //将失衡节点作为新的根节点的右子节点
    Root->right = node;

    //新根节点如果存在右子树则转到旧根节点左子树下
    node->left = Temp;

    //修正节点高度
    node->height = max(GetNodeHeight(node->left), GetNodeHeight(node->right)) + 1;
    Root->height = max(GetNodeHeight(Root->left), GetNodeHeight(Root->right)) + 1;

    return Root;
}

//创建节点
Node* NewNode(int value)
{
    Node* node = malloc(sizeof(Node));
    if (node == NULL) return NULL;
    memset(node, 0, sizeof(Node));
    node->value = value;
    node->height = 1;
    node->left = NULL;
    node->right = NULL;
    return node;
}

//插入节点
Node* Insert(Node* Root, int value)
{
    //空的结构
    if (Root == NULL) return NewNode(value);

    //节点关联
    if (Root->value > value)
    {
        Root->left = Insert(Root->left, value);
    }
    else if (Root->value < value)
    {
        Root->right = Insert(Root->right, value);
    }
    else
    {
        return Root;
    }

    //节点高度
    Root->height = max(GetNodeHeight(Root->left), GetNodeHeight(Root->right)) + 1;

    //节点失衡
    int nBalance = GetNodeBalanceFactor(Root);

    //左左
    if (nBalance > 1 &&  value < Root->left->value)
    {
        return RightRotate(Root);
    };

    //右右
    if (nBalance < -1 && value > Root->right->value)
    {
        return LeftRotate(Root);
    }

    //左右
    if (nBalance > 1 && value > Root->left->value)
    {
        Root->left = LeftRotate(Root->left);
        return RightRotate(Root);
    }

    //右左
    if (nBalance < -1 && value < Root->right->value)
    {
        Root->right = RightRotate(Root->right);
        return LeftRotate(Root);
    }

    return Root;
}

int main()
{
    Node* Root = NULL;
    Root = Insert(Root, 30);
    Root = Insert(Root, 20);
    Root = Insert(Root, 25);

    return 0;
}

示例代码

原文地址：https://blog.csdn.net/2301_80612536/article/details/140163579

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

上一篇：Kafka第四篇——生产数据总体概括，源码解析分区策略，数据收集器，Sender发送线程，key值
下一篇：驾校管理系统设计

Java项目:校园宿舍管理系统(优质版)(Springboot3+Maven+Mybatis Plus+Vue3+ Element Plus+Mysql)
Springboot3+Maven+Mybatis Plus+Vue3+ Element Plus+Mysql 开发的前后端分离的校园宿舍管理系统。
阅读更多2024-11-16
IntelliJ IDEA新建项目或导入未识别为maven解决
1.首先，我的情况是我新建了一个springboot项目，然后选择类型是Maven但是建立后不是maven项目。当然，前提是你的maven已经在idea上做好配置了。2.打开项目后，从File --》
阅读更多2024-11-16
Gin HTML 模板渲染
Gin HTML模板入门
阅读更多2024-11-16
未来的车网互动如何重塑我们的城市生活
设想一下，在一个寒冷的冬日，你的车辆通过车网互动得知前方桥梁可能结冰，它会自动降低速度，并提醒你注意驾驶安全。公众的参与同样重要，只有当越来越多的车辆加入到车网互动系统中，才能真正发挥其潜力，提高整个
阅读更多2024-11-16
人工智能技术的应用前景及其对生活和工作方式的影响
人工智能技术的应用前景广阔，它不仅在医疗、企业和日常生活中带来了显著的变化，还将继续推动社会的创新和发展。面对 AI 技术带来的机遇和挑战，我们需要共同努力，确保技术的发展能够造福人类社会，创造一个更
阅读更多2024-11-16
《AI技术，让生活更简单》
想象一下，你回到家，灯自动亮了，空调调到你喜欢的温度，冰箱告诉你牛奶快没了，甚至还能帮你预约超市送货。这不是科幻电影，这就是AI技术正在做的事情。
阅读更多2024-11-16
sychronized锁
sychronized 关键字能成为锁的原因，是因为它提供了**内置锁（Intrinsic Lock）**机制，用于线程同步，确保同一时刻只有一个线程能够访问被标记为 synchronized 的代码
阅读更多2024-11-16
SpringBoot 2.2.10 无法执行Test单元测试
同样的Idea版本，现有的项目却可以执行，按照C老师的提示增加对junit5的引用支持，依然没有，StackOverflow上也是提示增加依赖，依赖加完之后执行报错一个 EnginListener N
阅读更多2024-11-16
springMVC 全局异常统一处理
进⾏异常处理，具有集成简单、有良好的扩展性、对已有代码没有⼊侵性等优点，但该⽅法仅能获取到异常信息，若在出现异常时，对需要获取除异常以外的数据的情况不适⽤。Unchecked Exception，⽽
阅读更多2024-11-16
thinkphp6配置多应用项目及多域名访问路由app配置
ThinkPHP 多应用模式初探
阅读更多2024-11-16

数据结构 - C/C++ - 树

树的概念

结构特性

树的样式

树的存储

树的遍历

节点增删

二叉搜索树

平衡二叉树

相关文章