自学内容网 自学内容网
自学内容网 > 正文

MATLAB常用语句总结7

🕗 发布于 2024-07-08 17:01 matlab  算法  开发语言  

MATLAB总结7：常见错误归纳

本篇专门用于记录一些应试技巧

文章目录

前言

记忆力比较差，把学习过程中常用的语法记录于此，方便回忆时索引

一、一些小定义和小技巧

  1. rand的使用

rand 是用于生成在（0，1）上随机数的函数，而后面加入 rand(1,2)，则意为一个一行两列的（0，1）矩阵，不可乱加。需要使用不同范围的随机数则使用 A*rand() 即可

    x=5*rand();
    y=5*rand();
  1. 符号
取余：mod(A,b)%A是要进行取余的数字，b是除数
不等于：~=

  1. find()的使用
    用r=find(A<=0.6)，直接找到A中小于0.6的下标

  2. 分段函数的使用

y=(x<=8).* (2*x)+(x>8&&x<12).*(3*x)+(x>12).* (4*x);
  1. upper, lower的大小写转换
for i=1:length(v)
    if v(i)=='a'
        r(i)=upper(r(i));
    elseif v(i)=='h'
        r(i)='2';
    elseif v(i)=='v'
        r(i)='3';
    end
end

二、蒙塔卡罗求解方法

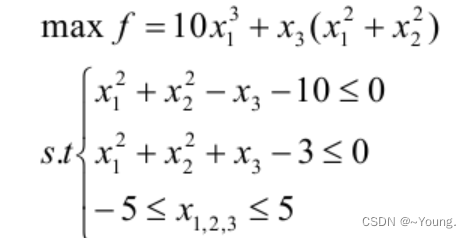
在这里插入图片描述

1.函数的定义

代码如下（示例）：

function c=myobj(x)
c=10*x(1)^3+x(3)*(x(1)^2+x(2)^2);
function r=mycon(x)
r=[x(1)^2+x(2)^2-x(3)-10 ; x(1)^2+x(2)^2+x(3)-3];
function m=myrand
while 1
    m=[10*rand-5 ;10*rand-5 ;10*rand-5 ];
    if mycon(m)<=0
        return 
    end
end

2.函数引用

代码如下（示例）：

function [val,x]=myfun2
rand('seed',11);

betterx=myrand;
betterval=myobj(betterx);

for i=1:10000
    betterx=myrand;
    if myobj(betterx)>betterval;
        betterval=myobj(betterx);
    end
end
x=double(betterx);
val=double(betterval);

3.代码量较少的蒙塔卡罗

function [val,x]=myfun2
rand('seed',11);
val=0;
for i=1:100000
    s=-10*rand(1,3)+5;
    if s(1)^2+s(2)^2-s(3)-10<=0 && s(1)^2+s(2)^2+s(3)-3<=0
        if 10*s(1)^3+s(3)*(s(1)^2+s(2)^2)>val
            val=10*s(1)^3+s(3)*(s(1)^2+s(2)^2);
            x=s;
        end
    end
end

三、函数引用与多变量

要分清多元函数的变量要用循环引用

代码如下（示例）：

function v=testmain
x=-2:0.1:2;
v=fun(x);

function r=fun(x)
for i=1:length(x)
    if x(i)<-1
        r(i)=x(i)^2+2*x(i)+1;
    elseif x(i)>-1 && x(i)<=2
        r(i)=3*x(i);
    else
        r(i)=2*sqrt(x(i));
    end
end

四、矩阵引用

引用矩阵可以用行列索引，也可以单行单列（注意单行单列是逗号），而且引用矩阵必须是括号

代码如下（示例）：

A(1,:)%引用第一行
A(:,2)%引用第二列

A(1,:)=A(1,:).^2;%给矩阵赋值要明白给谁赋值

五、非线性函数：fmincon的使用

  1. 使用时要注意哪里是只输入系数，哪里是方程
  2. 求最小值的是方程，其他的都只输出系数
  3. 同种变量用逗号隔开，不同种用分号
  4. 注意noncon的位置是使用@，引用里面有（）
  5. lb ub里面是逗号
  6. 函数系数的对应关系

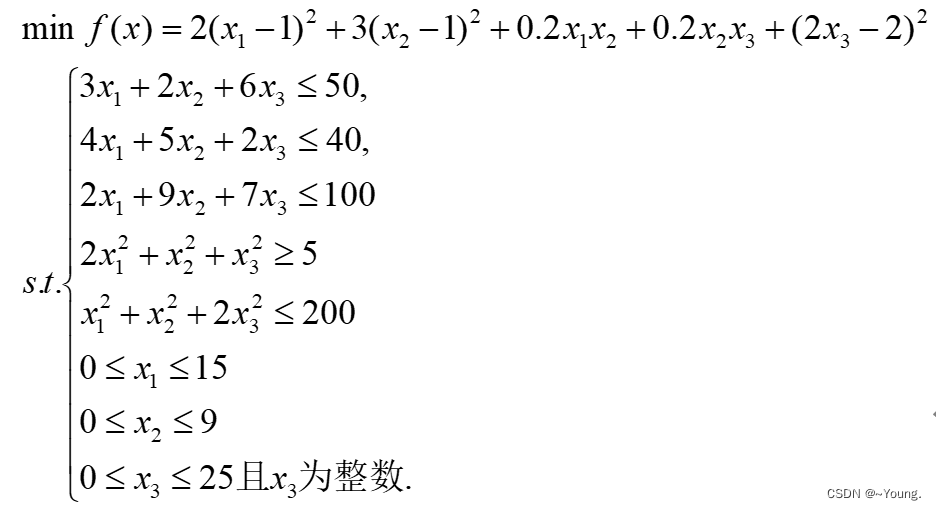
在这里插入图片描述

代码如下（示例）：

function [min,val]=fun3
Fun=@(x) 2*(x(1)-1)^2+3*(x(2)-1)^2+0.2*x(1)*x(2)+(2*x(3)-2)^2
A=[3 2 6;4 5 2;2 9 7];
b=[50;40;100];
Lb=[0,0,0];
ub=[15,9,25];
[min,val]=fmincon(Fun,[0,0,0],A,b,[],[],Lb,ub,@noncon);
function [c,ceq]=noncon(x)
c=[-2*x(1)^-x(2)^2-x(3)^2+5,
    x(1)^2+x(2)^2+2*x(3)^2-200];
ceq=[0];

六、线性规划函数

1.linprog

求解常规线性规划
注意！！！f 函数调用是系数

代码如下（示例）：
在这里插入图片描述

function [x,fval]=myfun19
f=[3,-4,2];
A=[1 -1 1;3 2 4;3 2 0];
b=[10;22;10];
Aeq=[];
beq=[];
lb=[0,0,0];
ub=[inf,inf,inf];
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub);

2.fminbnd、fminsearch

用于找到极小值，fminbnd找到区间内，fminsearch找到从某一点开始的极小值
fminbnd

[x，val] = fminbnd(fun, x1, x2)

% 定义要最小化的函数
fun = @(x) x^2 + 2*x + 1;

% 在区间[-2, 2]内寻找最小值
[x,val] = fminbnd(fun, -2, 2);

fminsearch

% 定义要最小化的函数
fun = @(x) x(1)^2 + x(2)^2;

% 指定初始点
x0 = [1, 1];

% 在多维空间中寻找最小值
x = fminsearch(fun, x0);

七、积分和微分

1.quad积分

y=@(x) (3.*x+2)./(x.^3+2.*x+5);
r=quad(y,0,3);

2.积分int 微分diff

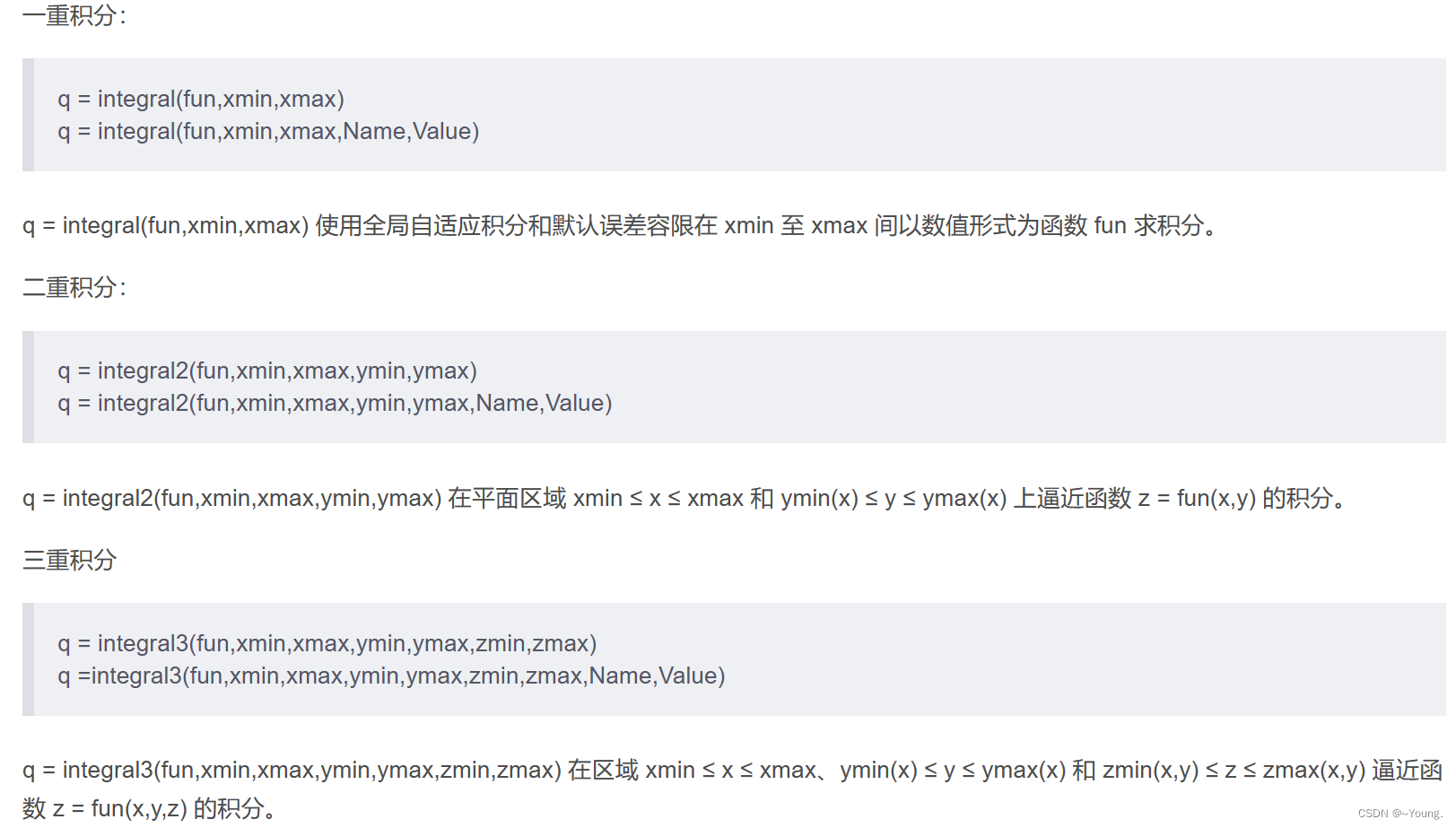
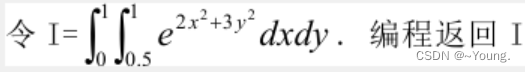
在这里插入图片描述
在这里插入图片描述

F=@(x,y) exp(2*x.^2+3*y.^2);
I=integral2(F,0.5,1,0,1);%取值范围

八、lsqcurvefit

  1. xdata，ydata储存数据，x(i)存放未知变量
  2. 调用时要把 fun(x,xdata) 全部带上
  3. 注意调用时，x和x1的意义是已经计算的系数和要代入计算的函数值，他们的位置和使用fun时的位置相对应！！！

代码如下（示例）：

xdata=[10.03,20.04,30.23,40.37,50.16,60.4,70.3,80.66,90.69,100.16,110.94,121.18,130.66,141.23,150.88,160.24];
ydata=[50.44,82.95,133.07,202.76,286.39,381.34,467.36,540.54,591.7,624.28,647.62,660.77,668.06,672.83,675.36,676.82];
fun = @(x,xdata) x(1)./(1+((x(1)/x(2))-1).*exp(-x(3)*xdata));
x0 = [1,1,1];
x = lsqcurvefit(fun,x0,xdata,ydata);
x1=[150:0.5:190];
y=fun(x,x1);

九、矩阵求解

  1. 可以使用linsolve
  2. 也可以求逆
  3. 或者是符号“\”
    在这里插入图片描述

代码如下（示例）：

a=[1 1 -1 2;
    -1 -2 1 -3;
    1 1 1 -3;
    2 1 -3 1];
e=[-3;1;-7;4];
x=inv(a)*e;

a=[1 1 -1 2;
    -1 -2 1 -3;
    1 1 1 -3;
    2 1 -3 1];
e=[-3;1;-7;4];
x=linsolve(a,e);


a=[1 1 -1 2;
    -1 -2 1 -3;
    1 1 1 -3;
    2 1 -3 1];
e=[-3;1;-7;4];
x=a\e;

十、polyfit 函数进行多项式拟合

  1. p = polyfit(x, y, n);
  2. x 是数据点的 x 值（自变量）向量，y 是数据点的 y 值（因变量）向量，n 是要拟合的多项式的次数。
  3. polyval(p,50); 用于计算特定位置的值

代码如下（示例）：

% 示例数据点
t=[1,6,11,16,21,26,31,36];
x=[5.35,10.51,15.664,20.76,25.94,30.08,35.22,40.36];
p=polyfit(t,x,1);
val=polyval(p,50);
r=[p,val];

十一、ode23和ode45

  1. 使用myode时，注意输入要把x，y都带上，先是自变量，后是因变量
  2. y(1)可表示y，y(2)可表示一阶导数
  3. 输出 [t,y] 分别是对应时间点和对应时间的输出值

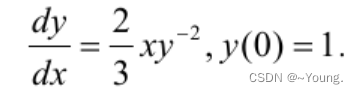
在这里插入图片描述

y1 = 0:0.01:1;%取值范围
y0 = 1;初值
[t,y] = ode23(@myode, y1, y0);

function dydx=myode(x,y)
    dydx=(2/3)*x/y^2;

function r = myfun
    x1 = 0:0.1:100;%定义范围
    x0 = [2; 0]; %定义初始条件
    [t, x] = ode23(@myode, x1, x0);%这里的x是一个向量
end

function dxdt = myode(t, x)
    dxdt = [20*(1-x(1)^2)*x(2) + 0.5*x(1); 0];%x(1)代表x，x(2)代表dx/dt
end

十二、fzero

x0 是初始猜测的根的值。

代码如下（示例）：

x = fzero(fun, x0)
x = fzero(fun, x0, options)

十三、meshgrid和surf

  1. 注意z的输出
  2. [x,y]=meshgrid(x取值,y取值)
  3. surf绘制表面图

代码如下（示例）：

function z=myfun24
[x,y]=meshgrid(-3:0.1:3,-3:0.1:3);
z=x.*y.*exp(sin(x.^2+y.^2));
surf(x,y,z);

十四、fsolve

  1. 记住两个公式：root2和fsolve的使用
  2. folsve(@root2,x0)
  3. f=root2(x) f(1)= f(2)=

代码如下（示例）：

% 示例数据点
function r=myfun29
x0=[0,0];
r=fsolve(@root2,x0);

function f=root2(x)
f(1)=x(1)^2-x(2)-1;
f(2)=(x(1)-2)^2+(x(2)-0.5)^2-1;

原文地址：https://blog.csdn.net/2302_77399562/article/details/140159215

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！

相关文章

自学内容网
Copyright © 2015-2024