最小二乘法拟合二维点

方法1：使用np.polyfit()函数进行拟合

import numpy as np
import matplotlib.pyplot as plt

# 模拟数据
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([1, 3, 2, 4, 7, 10, 11, 15, 17, 20])

# 使用多项式拟合，这里选择二次多项式
coefficients = np.polyfit(x, y, 2)
polynomial = np.poly1d(coefficients)
print(polynomial)
# 计算拟合的y值
y_fit = polynomial(x)

# 绘图展示结果
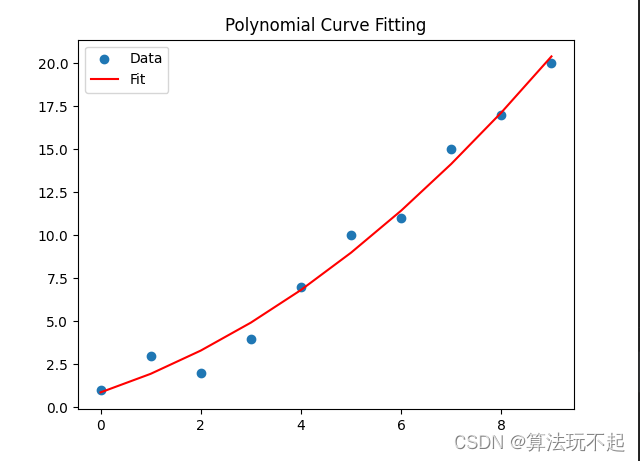
plt.scatter(x, y, label='Data')  # 原始数据点
plt.plot(x, y_fit, label='Fit', color='red')  # 拟合曲线
plt.title('Polynomial Curve Fitting')
plt.legend()
plt.show()

运行结果：

方法2：手动实现

import matplotlib.pyplot as plt
import numpy as np
# 模拟数据
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([1, 3, 2, 4, 7, 10, 11, 15, 17, 20])

# 计算x的各次幂的和
x_sum = sum(x)
x2_sum = sum(xi**2 for xi in x)
x3_sum = sum(xi**3 for xi in x)
x4_sum = sum(xi**4 for xi in x)

# 计算x和y的乘积的和
xy_sum = sum(xi*yi for xi, yi in zip(x, y))
x2y_sum = sum(xi**2*yi for xi, yi in zip(x, y))

# 构建正规方程的系数矩阵和常数项向量
A = [[len(x), x_sum, x2_sum],
     [x_sum, x2_sum, x3_sum],
     [x2_sum, x3_sum, x4_sum]]
b = [sum(y), xy_sum, x2y_sum]

# 解正规方程
# 使用克莱默法则（Cramer's Rule）求解
def cramer_solve(A, b):
    det_A = np.linalg.det(A)
    coefficients = []
    for i in range(len(b)):
        Ai = [row[:i] + [b[j]] + row[i+1:] for j, row in enumerate(A)]
        det_Ai = np.linalg.det(Ai)
        coefficients.append(det_Ai / det_A)
    return coefficients

a, b, c = cramer_solve(A, b)
print(a, b, c)
# 使用求得的系数计算拟合值
y_fit = [c*xi**2 + b*xi + a for xi in x]

# 绘图
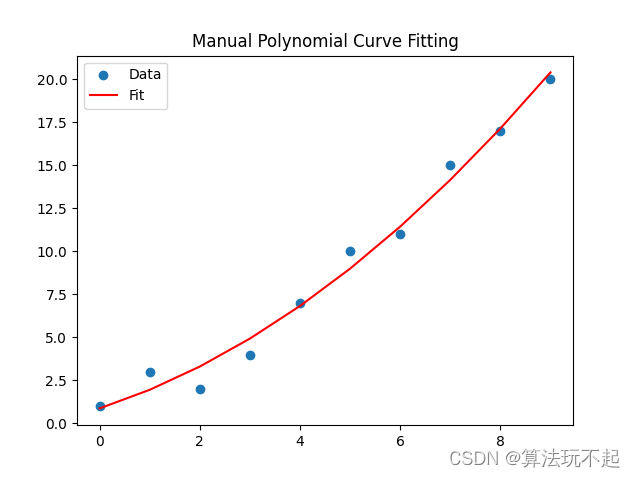
plt.scatter(x, y, label='Data')
plt.plot(x, y_fit, label='Fit', color='red')
plt.title('Manual Polynomial Curve Fitting')
plt.legend()
plt.show()

运行结果：

原文地址：https://blog.csdn.net/qq_18566467/article/details/135706512

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！