算法题总结(十三)—— 动态规划(上)
动态规划
动态规划理论基础
什么是动态规划
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
动态规划的解题步骤
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
动态规划应该如何debug
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
509、斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
1、确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2、确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
3、dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0;
dp[1] = 1;
4、确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5、举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
//非压缩状态的版本
class Solution {
public int fib(int n) {
if (n <= 1) return n;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int index = 2; index <= n; index++){
dp[index] = dp[index - 1] + dp[index - 2];
}
return dp[n];
}
}
70、爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
1、确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
2、确定递推公式
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
3、初始化
重要:
关于dp[0]的定义,由于dp[0]没有意义,所以从dp[1]开始,初始化dp[1]=1, dp[2]=2
class Solution {
public int climbStairs(int n) {
if(n==1||n==2)
return n;
int[] dp =new int[n+1];
dp[1]=1;
dp[2]=2;
for(int i=3;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
}
爬楼梯扩展
这道题目还可以继续深化,就是一步一个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种方法爬到n阶楼顶。这又有难度了,这其实是一个完全背包问题。
当做完全背包的求和问题:因为是排列问题,所以先遍历容量,在遍历物品,因为是完全背包,所以内循环小从小到大,然后容量大于物品时,dp[i]+=dp[i-j];
class Solution{
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { // 把m换成2,就可以AC爬楼梯这道题
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
746、使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
1、确定dp数组以及下标的含义
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
2、确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3、dp数组如何初始化
题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
4、确定遍历顺序:从前向后
5、模拟
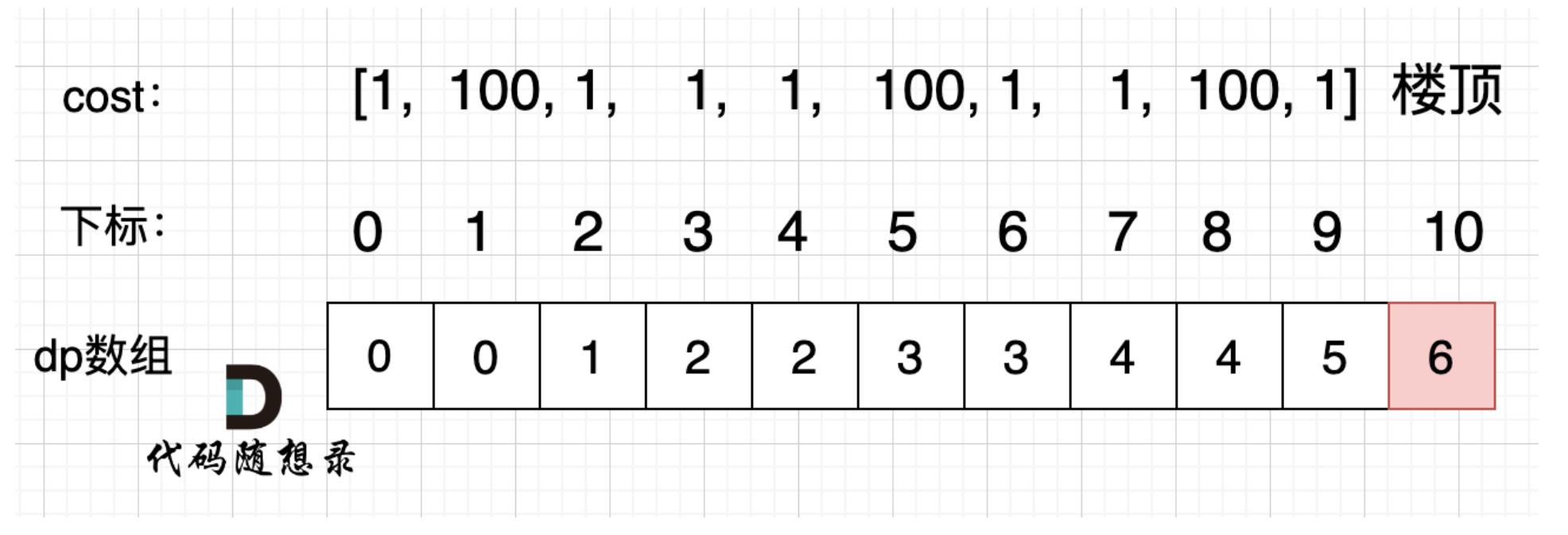
class Solution {
public int minCostClimbingStairs(int[] cost) {
int len = cost.length;
int[] dp = new int[len + 1];
// 从下标为 0 或下标为 1 的台阶开始,因此支付费用为0
dp[0] = 0;
dp[1] = 0;
// 计算到达每一层台阶的最小费用
for (int i = 2; i <= len; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[len];
}
}
62、不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
//初始化
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
63、不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
对比62、不同路径,如果有障碍,就是把对应的标记dp标记为0就可以。在初始化的时候,如果遇到了障碍,则后面的也都初始化为0
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
//如果在起点或终点出现了障碍,直接返回0
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 0; i < m; i++) {
if(obstacleGrid[0][0]==0)
dp[i][0] = 1;
else
break; //遇到障碍直接结束,后面都初始化为0
}
for (int j = 0; j < n; j++) {
if(obstacleGrid[0][j] == 0)
dp[0][j] = 1;
else
break;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
return dp[m - 1][n - 1];
}
}
64、最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
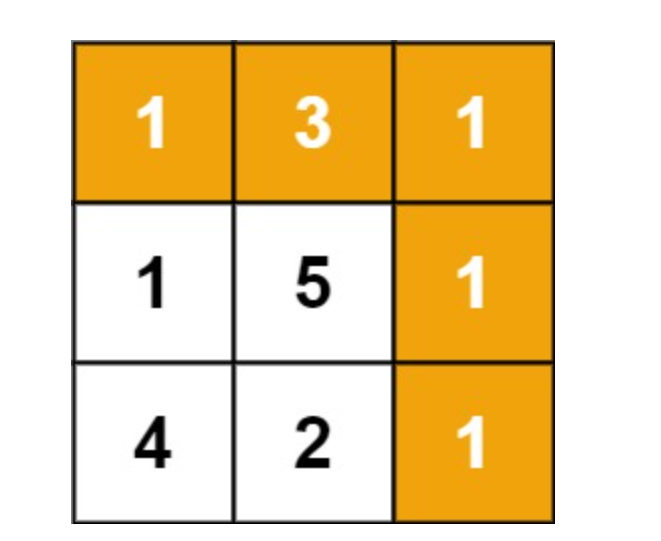
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
class Solution {
public int minPathSum(int[][] grid) {
int m=grid.length;
int n=grid[0].length;
int dp[][] =new int[m][n]; //表示最小的数字总和
//初始化
int sum=0;
for(int i=0;i<m;i++)
{
sum+=grid[i][0];
dp[i][0]=sum;
}
sum=0;
for(int j=0;j<n;j++)
{
sum+=grid[0][j];
dp[0][j]=sum;
}
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[m-1][n-1];
}
}
343、整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
class Solution {
public int integerBreak(int n) {
//dp[i] 为正整数 i 拆分后的结果的最大乘积
int[] dp =new int[n+1];
//初始化,dp[0]和dp[1]的初始化没有意义,因为0,1都无法拆开
dp[2]=1;
for(int i=3;i<=n;i++)
{
//只需要到i/2即可,因为拆成大小相近的数才能使乘积最大。
//即拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的
for(int j=1;j<=i/2;j++)
{
dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j])); //一定不要忘dp[i]也要比较
// j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ,再相乘
//而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
}
}
return dp[n];
}
}
96、不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
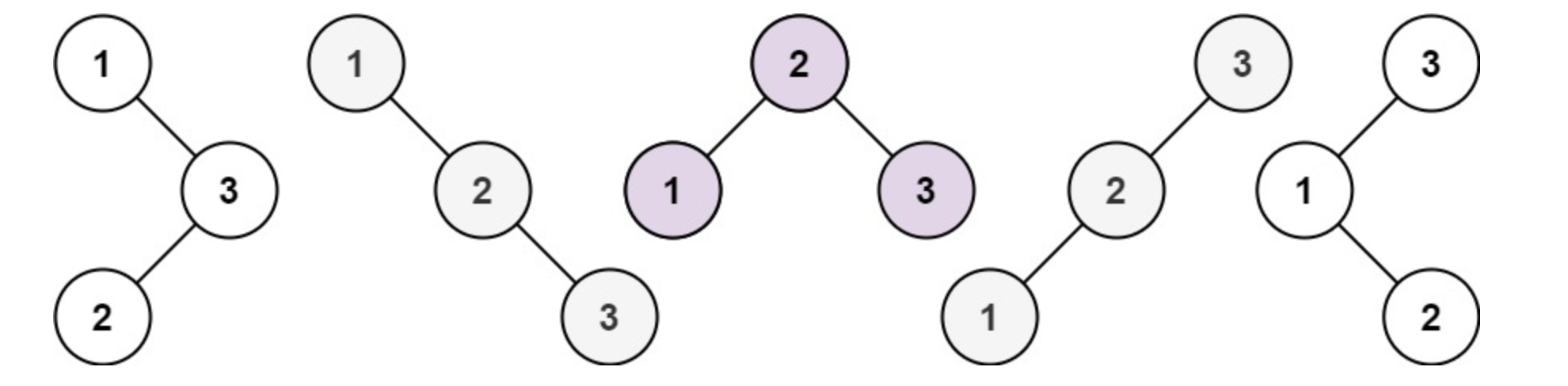
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
其实就是求n个结点,构成的二叉树的数目,有多少个。因为二叉树确定了,只需要填数字,就变为二叉搜索树。
dp[i]就是i个结点能构成的二叉树的数目
递推公式:
选取一个作为根结点,剩下的i-1个结点,进行分配,左节点的个数依次是0到i-1,右节点的个数是i-1到0;
即j是从1到i
dp[i]+=dp[j-1]*dp[i-j];
class Solution {
public int numTrees(int n) {
//实际上就是求n个结点能构成的二叉树的数目
//因为我们求出后只需填数字就可以
//定义为 i个结点能组成的二叉树的数目
int[] dp =new int[n+1];
dp[0]=1; //为了让后面相乘不为0
dp[1]=1;
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
//一共i个结点,选取1个做根,然后剩下的i-1个分到左右子树
//即左子树结点依次为:0到i-1个
//右子树的结点为i-1到0
dp[i]+=dp[j-1]*dp[i-j];
}
}
return dp[n];
}
}
01背包理论基础
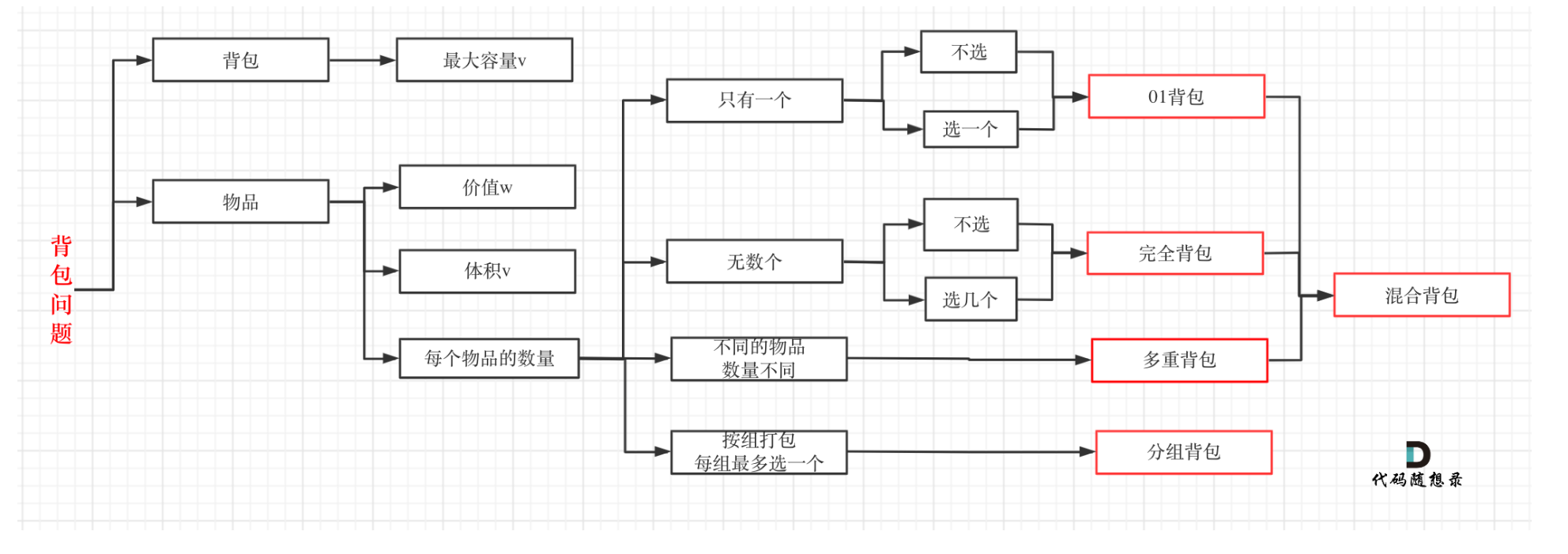
重点:01背包和完全背包
1、确定dp数组以及下标的含义
使用二维数组,即dp[i] [j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2、确定递推公式
那么可以有两个方向推出来,即放物品i和不放物品i
所以递归公式:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
3、初始化
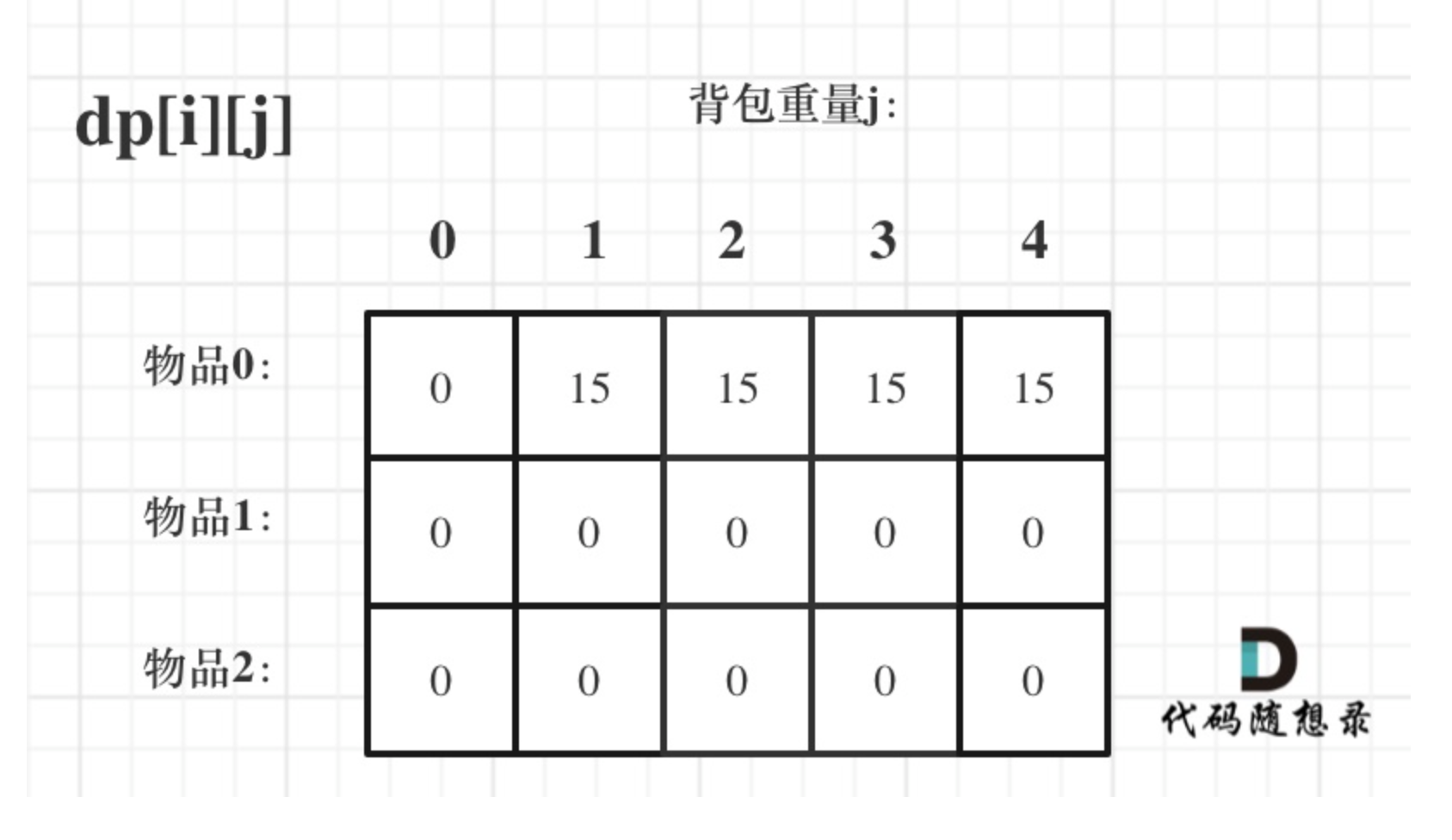
如果背包容量j为0的话,即dp[i] [0],无论是选取哪些物品,背包价值总和一定为0
由递推公式可知需要初始化dp[0],
那么很明显当 j < weight[0]的时候,dp[0] [j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0] [j] 应该是value[0],因为背包容量放足够放编号0物品。
4、遍历顺序
因为从递推公式可以看出,dp依赖的是左上角以及上方的数值,所以一行一行遍历和一列一列遍历都是可以的,所以先遍历物品还是先遍历背包都是可以的!
public class BagProblem {
public static void main(String[] args) {
int[] weight = {1,3,4};
int[] value = {15,20,30};
int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp数组
int goods = weight.length; // 获取物品的数量
int[][] dp = new int[goods][bagSize + 1];
// 初始化dp数组,其余的都是0
// 创建数组后,其中默认的值就是0
for (int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
// 填充dp数组
for (int i = 1; i < weight.length; i++) {
for (int j = 1; j <= bagSize; j++) {
if (j < weight[i]) {
/**
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
*/
dp[i][j] = dp[i-1][j];
} else {
/**
* 当前背包的容量可以放下物品i
* 那么此时分两种情况:
* 1、不放物品i
* 2、放物品i
* 比较这两种情况下,哪种背包中物品的最大价值最大
*/
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
}
}
}
// 打印dp数组
for (int i = 0; i < goods; i++) {
for (int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + "\t");
}
System.out.println("\n");
}
}
}
01背包理论基础(滚动数组)
使用一维数组
1、确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2、递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3、初始化
都初始化为0,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
4、遍历顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
01背包的一维数组,背包为什么要倒叙遍历?
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。即二维数组,从上到下 是从右向左遍历的。
即只用倒序遍历,才能使用一维数组模拟二维数组。
背包倒序遍历是为了保证每个物品i只被放入一次!多重背包的话是从小到大的遍历!,因为计算dp[j]的时候,是用到dp[j - weight[i]],如果正序遍历,那每一个物品会被放入多次!
不能先遍历背包在遍历物品,因为一维数组,背包容量一定是要倒序遍历,因为只有倒序遍历才能利用一维数组,如果遍历背包容量放在上一层,那么对每个背包dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWight = 4;
testWeightBagProblem(weight, value, bagWight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int wLen = weight.length;
//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值
int[] dp = new int[bagWeight + 1];
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 0; i < wLen; i++){
for (int j = bagWeight; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
//打印dp数组
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
416、分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
转化为01背包问题:
- 背包的容量为sum / 2,即判断能否把背包装满即可
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集, 即dp[target]==target,因为装的时候是尽可能的装的最大
- 背包中每一个元素是不可重复放入,说明是01背包问题。
class Solution {
public boolean canPartition(int[] nums) {
int sum=0;
int n=nums.length;
for(int num:nums)
{
sum+=num;
}
if(sum%2==1)
return false;
int target=sum/2; //即背包的总容量
int[] dp=new int[target+1]; //dp数组是一直到target
for(int i=0;i<n;i++)
{
for(int j=target;j>=nums[i];j--)
{
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
//因为每次都是尽可能的装到最大,即尽可能的接近target,所以只需要判断最后的是否等于target
return dp[target]==target;
}
}
1049、最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果 x == y,那么两块石头都会被完全粉碎;
- 如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了
所以和上一题基本一样,最后dp[target]里是容量为target的背包所能背的最大重量。
那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum=0;
for(int stone:stones)
{
sum+=stone;
}
int target=sum/2; //容量为总和的一半,尽可能装到最大。
int[] dp=new int[target+1];
for(int i=0;i<stones.length;i++)
{
for(int j=target;j>=stones[i];j--)
{
dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return sum-2*dp[target];
}
}
494、目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
这道题目咋眼一看和动态规划背包啥的也没啥关系,本质上还是把数分为两部分
本题要如何使表达式结果为target,
既然为target,那么就一定有 left组合 - right组合 = target。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合。
此时问题就转化为,装满容量为left的背包,有几种方法。
注意之前的都是求装满背包的最大容量是多少。
因为 left = (target + sum)/2 ,所以 (target + sum)如果是奇数的话,是无解的,另外,如果target的绝对值大于sum的绝对值也是无解的。
1、确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
注意递推公式的含义是有多少种方法!
2、递推公式,组合类问题的递推公式是什么样的呢?
dp[j] += dp[j - nums[i]]
注意:求装满背包有几种方法类似的题目,递推公式基本都是这样的。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
3、初始化
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
dp[j]其他下标对应的数值也应该初始化为0,从递推公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。
4、遍历顺序
nums放在外循环,target在内循环,且内循环倒序。
即外循环遍历的时候,就相当于用0到i的物品来装容量为j的背包,j要倒序来装。 理解下图!
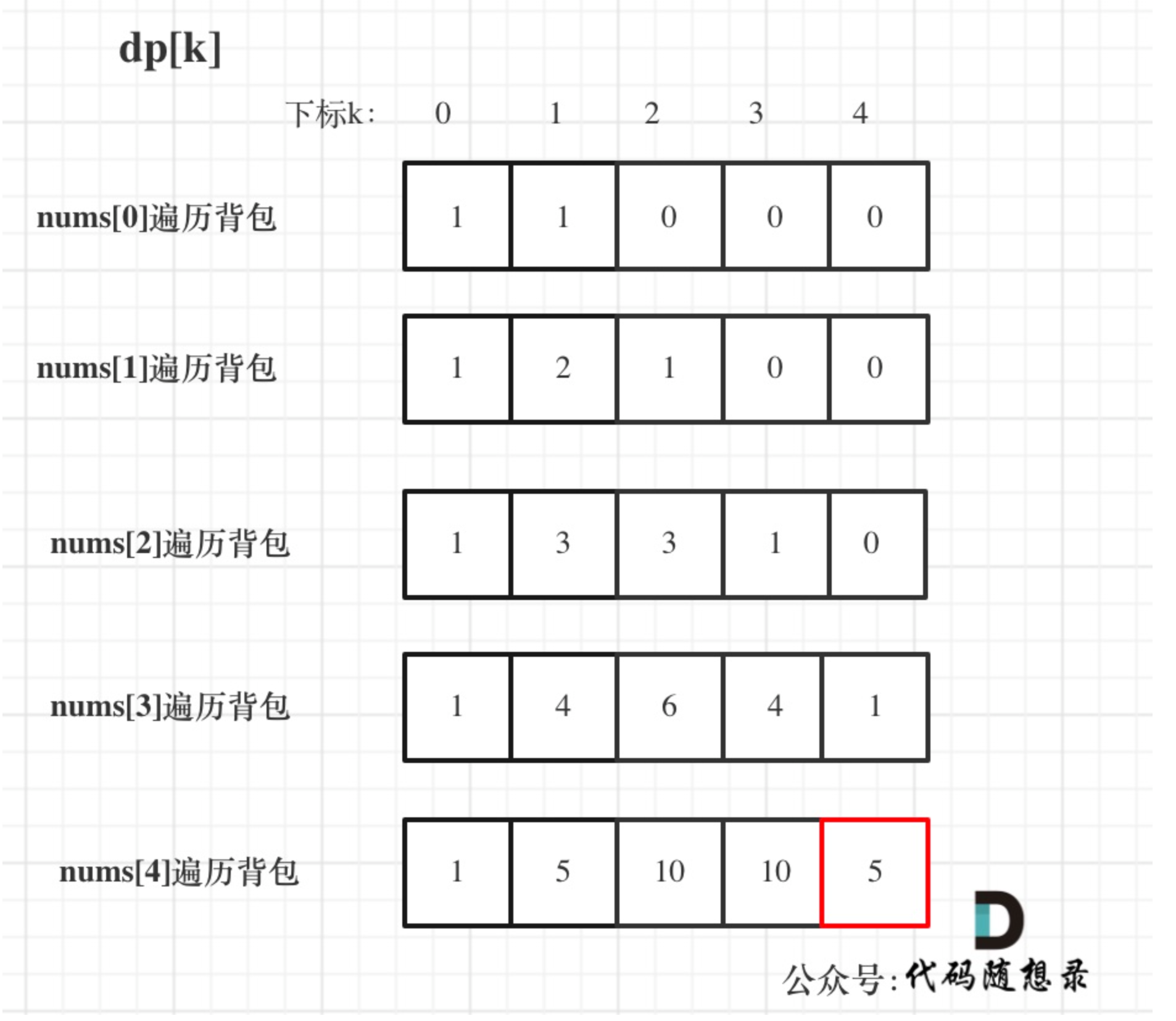
5、举例子
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum=0;
for(int num:nums)
{
sum+=num;
}
//(target + sum)如果是奇数的话,是无解的
if((sum+target)%2==1)
return 0;
if(Math.abs(target)>sum)
return 0;
int size = (target+sum)/2; //size不可能为负的,相当于背包的容量
int[] dp =new int[size+1];
dp[0]=1;
for(int i=0;i<nums.length;i++)
{
for(int j=size;j>=nums[i];j--)
{
dp[j]+=dp[j-nums[i]]; //可以把dp[j] 理解成不使用nums[i],dp[j-nums[i]]为使用nums[i],因为倒序遍历背包容量,是利用了i-1的基础上。
}
}
return dp[size];
}
}
二维的形式:
相当于二维形式的 递推公式:dp[i] [j] =dp[i-1] [j]+dp[i-1] [j-nums[i ]] , 一个使用 一个不使用
474、一零和
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
本题中strs 数组里的元素就是物品,每个物品都有两个维度!
而m 和 n相当于是一个背包,两个维度的背包。
所以还是背包问题!
注意使用的还是滚动数组,只不过是两个维度!
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
//dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
int[][] dp=new int[m+1][n+1];
for(String str:strs) //遍历物品
{
int zeroNum =0;
int oneNum=0;
//计算每个物品的容量
for(char ch:str.toCharArray())
{
if(ch=='0')
zeroNum++;
else if(ch=='1')
oneNum++;
}
//遍历背包
for(int i=m;i>=zeroNum;i--)
{
for(int j=n;j>=oneNum;j--)
{
//dp[i][j]是不选择物品str,dp[i-zeroNum][j-oneNum]+1是选择物品str
dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1); //倒序利用一维数组
}
}
}
return dp[m][n];
}
}
此时我们讲解了0-1背包的多种应用,
- 纯 0 - 1 背包 (opens new window)是求 给定背包容量 装满背包 的最大价值是多少。
- 416. 分割等和子集 (opens new window)是求 给定背包容量,能不能装满这个背包。
- 1049. 最后一块石头的重量 II (opens new window)是求 给定背包容量,尽可能装,最多能装多少
- 494. 目标和 (opens new window)是求 给定背包容量,装满背包有多少种方法。
- 本题是求 给定背包容量,装满背包最多有多少个物品。
完全背包理论基础
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历。
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。即,正序遍历的时候两个for循环的数量是无所谓的!
全文我说的都是对于纯完全背包问题,其for循环的先后循环是可以颠倒的!
//先遍历物品,再遍历背包
private static void testCompletePack(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){ // 遍历物品
for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
for (int j = 0; j < weight.length; j++){ // 遍历物品
if (i - weight[j] >= 0){
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
}
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
518、零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
即组合问题,递推公式为dp[j] += dp[j - coins[i]];
纯完全背包的两个for循环的先后顺序都是可以的。但本题就不行了!
关于遍历顺序的问题:
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
dp[j] += dp[j - coins[i]];
}
}
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
总结:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {
public int change(int amount, int[] coins) {
int[] dp=new int[amount+1];
dp[0]=1; //计数的时候初始化为0
for(int i=0;i<coins.length;i++)
{
for(int j=coins[i];j<=amount;j++)
{
dp[j]+=dp[j-coins[i]];
}
}
return dp[amount];
}
}
377、组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
但其本质是本题求的是排列总和,而且仅仅是求排列总和的个数,并不是把所有的排列都列出来。
如果本题要把排列都列出来的话,只能使用回溯算法爆搜。
动规五部曲分析如下:
1、确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
2、确定递推公式
dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导出来。
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
3、dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
4、遍历顺序
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp =new int[target+1];
dp[0]=1;
for(int j=1;j<=target;j++) //先遍历背包,在遍历物品
{
for(int i=0;i<nums.length;i++)
{
if(j>=nums[i]) //要保证容量大于等于物品
dp[j]+=dp[j-nums[i]];
}
}
return dp[target];
}
}
70、爬楼梯进阶版-ACM模式
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入描述:输入共一行,包含两个正整数,分别表示n, m
输出描述:输出一个整数,表示爬到楼顶的方法数。
输入示例:3 2
输出示例:3
提示:
当 m = 2,n = 3 时,n = 3 这表示一共有三个台阶,m = 2 代表你每次可以爬一个台阶或者两个台阶。
此时你有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶段
- 1 阶 + 2 阶
- 2 阶 + 1 阶
我们之前做的 爬楼梯 是只能至多爬两个台阶,采用的是最直接的动规方法(斐波那契)。
这次改为:一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
这又有难度了,这其实是一个完全背包问题。
1阶,2阶,… m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
此时大家应该发现这就是一个完全背包问题了!
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
排列问题先遍历背包,再遍历物品。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
import java.util.Scanner;
class climbStairs{
public static void main(String [] args){
Scanner sc = new Scanner(System.in);
int m, n;
while (sc.hasNextInt()) {
// 从键盘输入参数,中间用空格隔开
n = sc.nextInt();
m = sc.nextInt();
// 求排列问题,先遍历背包再遍历物品
int[] dp = new int[n + 1];
dp[0] = 1;
for (int j = 1; j <= n; j++) {
for (int i = 1; i <= m; i++) {
if (j - i >= 0) dp[j] += dp[j - i];
}
}
System.out.println(dp[n]);
}
}
}
322、零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
动规五部曲分析如下:
1、确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2、确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
3、dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
4、确定遍历顺序
本题求钱币最小个数,你那么先遍历钱币和先遍历背包都是可以的,都不影响钱币的最小个数。
5、举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例
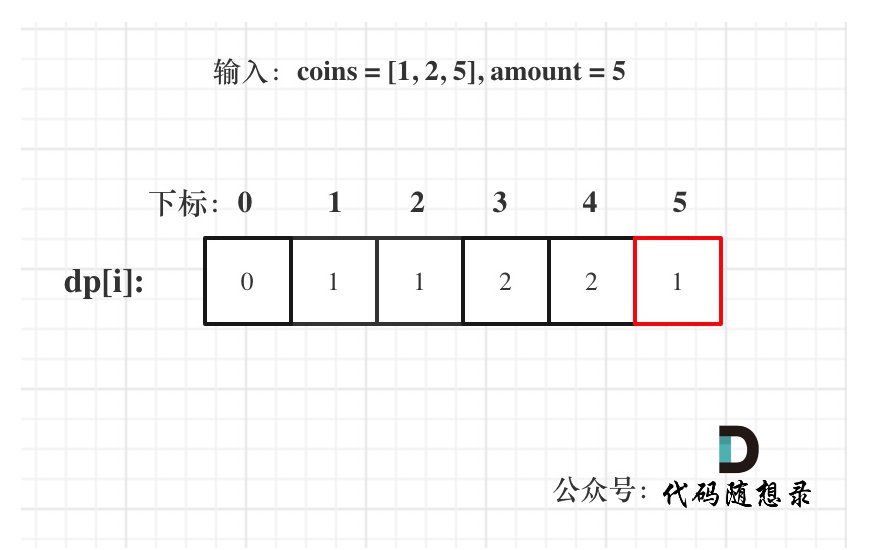
根据先遍历硬币,在遍历背包,模拟出过程:
coins[0]=1: 0 1 2 3 4 5
coins[1]=2: 0 1 1 2 2 3
coins[2]=5: 0 1 1 2 2 1
完全背包的求最小值问题:
不一定能凑成。
class Solution {
public int coinChange(int[] coins, int amount) {
int max = Integer.MAX_VALUE;
int[] dp = new int[amount + 1];
//初始化dp数组为最大值
for (int j = 1; j < dp.length; j++) {
dp[j] = max;
}
//当金额为0时需要的硬币数目为0
dp[0] = 0; //dp[0]要初始化,因为后面会用到
for (int i = 0; i < coins.length; i++) {
//正序遍历:完全背包每个硬币可以选择多次
for (int j = coins[i]; j <= amount; j++) {
//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
if(dp[j - coins[i]] != max)
//选择硬币数目最小的情况
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == max ? -1 : dp[amount];
}
}
279、 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
我来把题目翻译一下:完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
递推公式:所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
完全背包的求最小值问题:
本题一定能凑成。
class Solution {
public int numSquares(int n) {
int max=Integer.MAX_VALUE;
int[] dp=new int[n+1]; //n相当于背包的重量
for(int i=1;i<dp.length;i++)
{
dp[i]=max;
}
dp[0]=0;
for(int i=1;i<=Math.sqrt(n);i++) //i相当于物品
{
for(int j=i*i;j<=n;j++) //j要从i*i开始,是背包容量
{
if(dp[j-i*i]!=max) //dp[j-i*i] 不是初始值的时候
dp[j]=Math.min(dp[j],dp[j-i*i]+1);
}
}
return dp[n];
}
}
139、单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
1、确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
2、确定递推公式
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
3、dp数组如何初始化
从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。
4、遍历顺序
不同的顺序组成的单词不同,所以是排列问题。
字符串s相当于背包,字符串列表相当于每个物品。
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp=new boolean[s.length()+1];
dp[0]=true;
//因为是有序的,先遍历背包,在遍历物品
for(int i=1;i<=s.length();i++)
{
for(String word:wordDict)
{
int len=word.length();
//因为先遍历背包的,因此容量要大于len
if(i>=len &&dp[i-len] && word.equals(s.substring(i-len,i)))
{
dp[i]=true;
}
}
}
return dp[s.length()];
}
}
背包问题总结
在讲解背包问题的时候,我们都是按照如下五部来逐步分析,相信大家也体会到,把这五部都搞透了,算是对动规来理解深入了。
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
其实这五部里哪一步都很关键,但确定递推公式和确定遍历顺序都具有规律性和代表性,所以下面我从这两点来对背包问题做一做总结
递推公式:
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
遍历顺序:
01背包
在动态规划:关于01背包问题,你该了解这些! (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
和动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的,大家需要注意!
完全背包
说完01背包,再看看完全背包。
在动态规划:关于完全背包,你该了解这些! (opens new window)中,讲解了纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
- 求组合数:动态规划:518.零钱兑换II(opens new window)
- 求排列数:动态规划:377. 组合总和 Ⅳ (opens new window)、动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了。
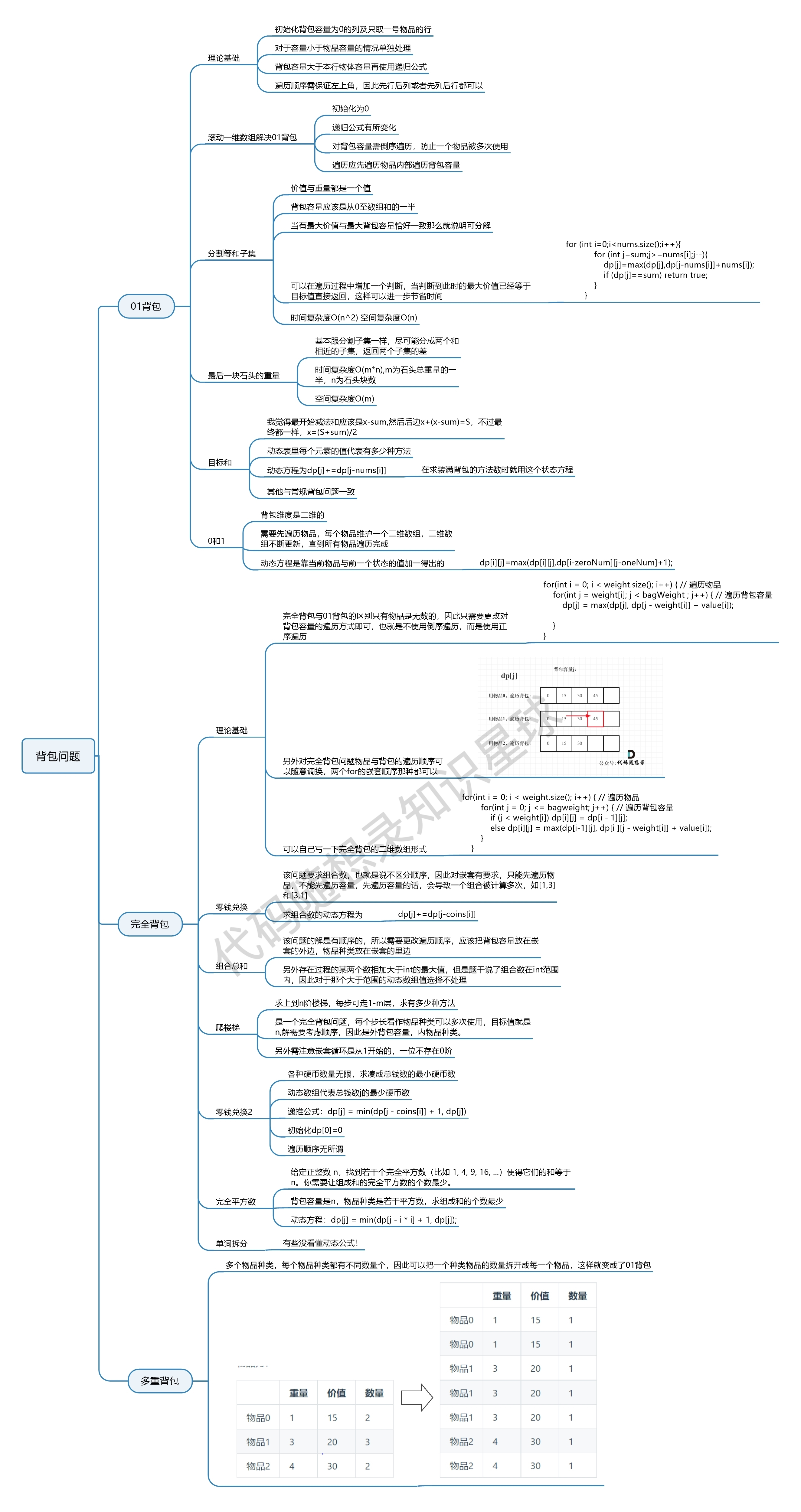
即:
一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。完全背包与01背包的区别就是,完全背包的背包容量要从小到大正序遍历。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
做题的时候要从四个方面考虑,dp的定义,递归函数、初始化,遍历顺序
原文地址:https://blog.csdn.net/maruofan666/article/details/142994563
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
