数据结构-5.二叉树
本篇博客给大家带来的是二叉树的知识点, 其中包括面试经常会提问的真题 ArrayList 和 LinkedList 的区别 .
文章专栏: Java-数据结构
若有问题 评论区见
欢迎大家点赞 评论 收藏 分享
如果你不知道分享给谁,那就分享给薯条。
你们的支持是我不断创作的动力 .
1. 二叉树
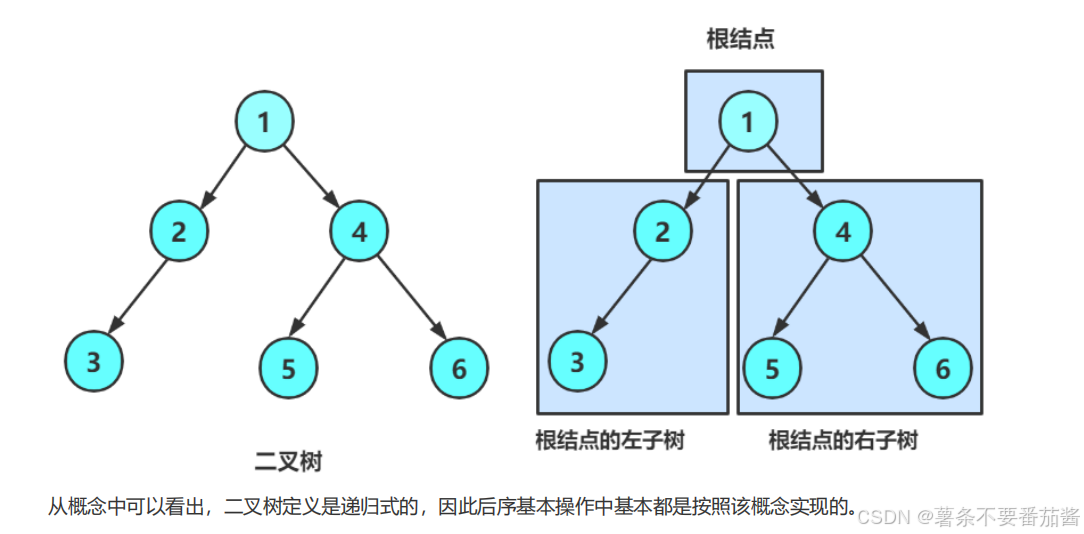
1.1 二叉树的概念
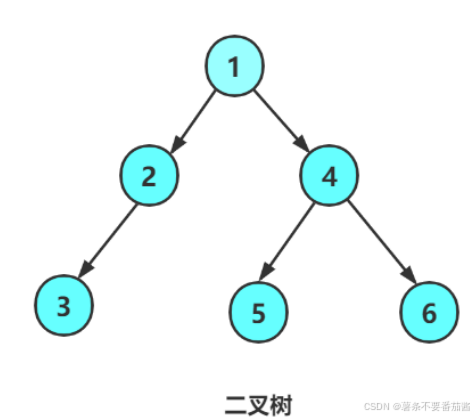
1.2 两种特殊的二叉树
1. 满二叉树: 一颗二叉树, 如果每层的结点数都达到最大值, 则这颗二叉树就是满二叉树. 若满二叉树的层数为K, 那么其节点总数是 2^k - 1.

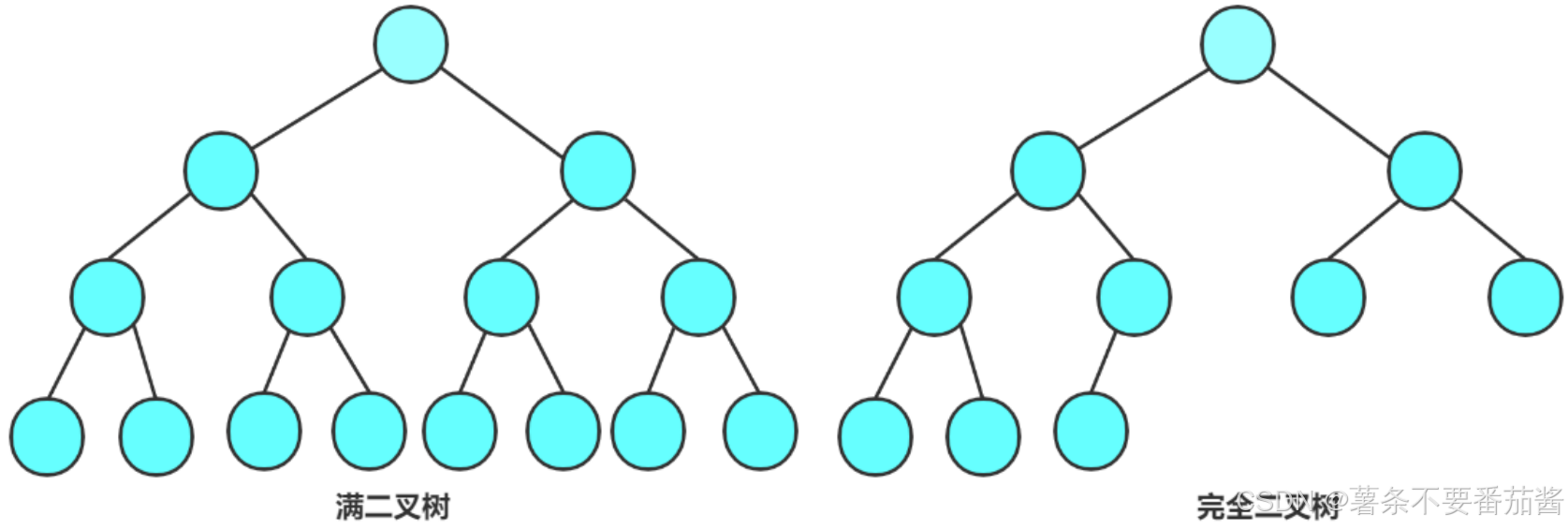
1.3二叉树的性质
1.4 二叉树的存储
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}1.5 二叉树的基本操作
1.5.1 二叉树的简单创建
public class BinaryTree {
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public void createTree() {
TreeNode A = new TreeNode(4);
TreeNode B = new TreeNode(2);
TreeNode C = new TreeNode(7);
TreeNode D = new TreeNode(1);
TreeNode E = new TreeNode(3);
TreeNode F = new TreeNode(6);
TreeNode G = new TreeNode(9);
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
}
}
1.5.2 二叉树的遍历
1. 前中后序遍历
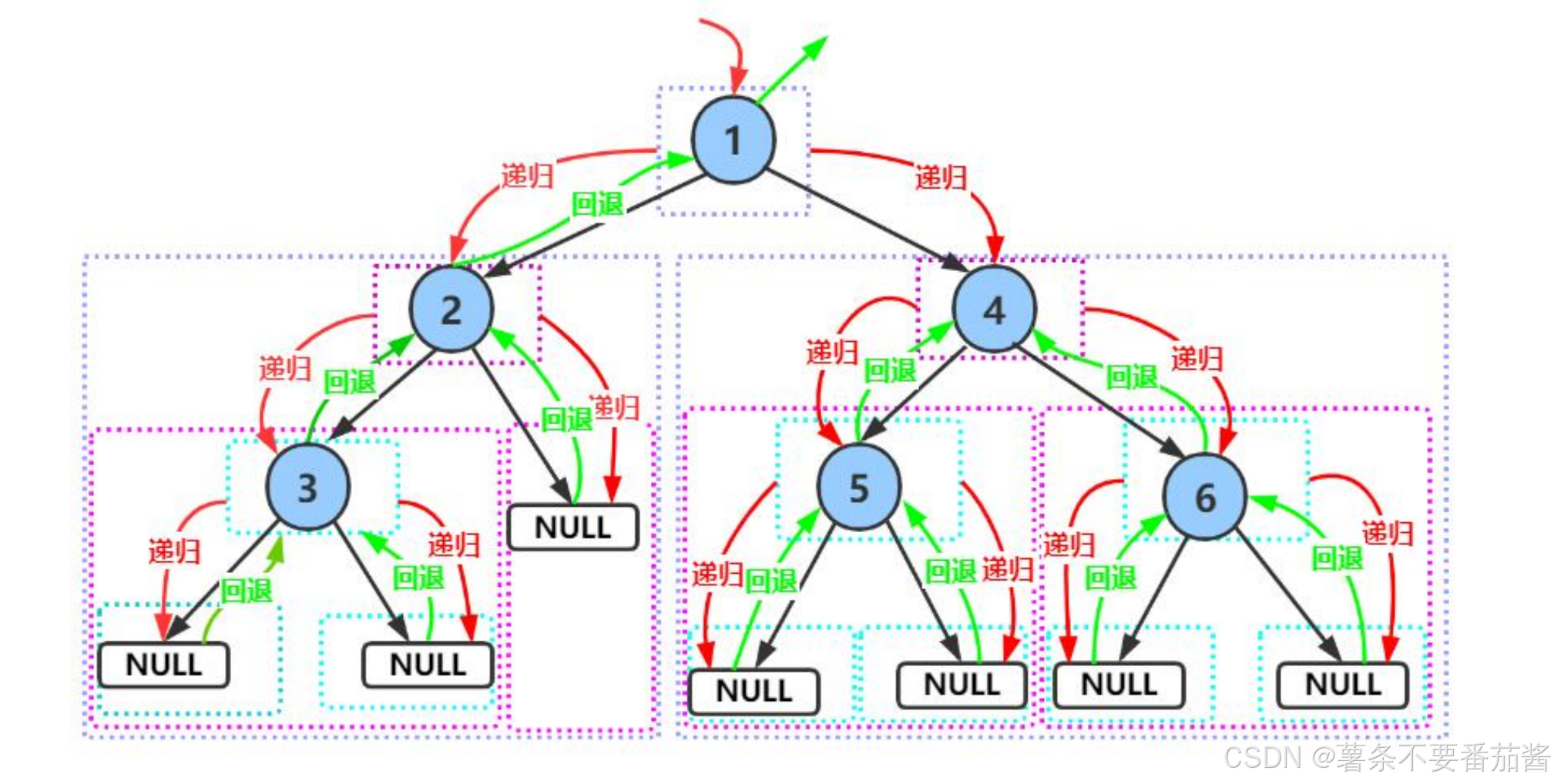
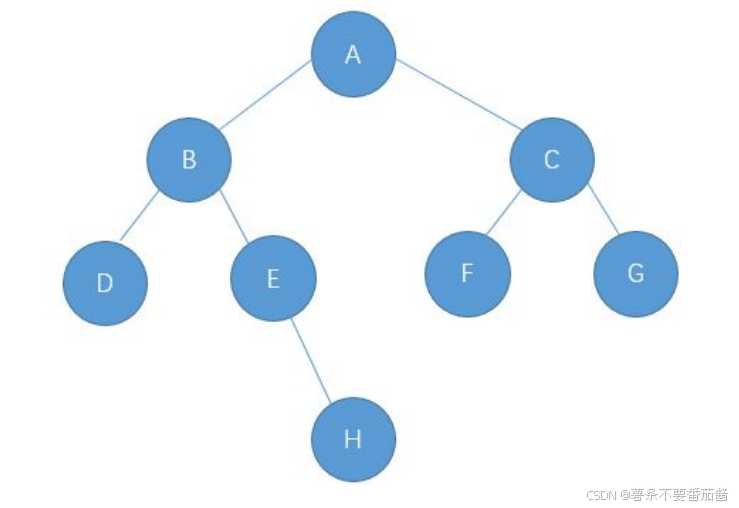

//前序遍历: 根 左 右
public void preOrder(TreeNode root) {
if(root == null) return;//终止条件
//前序遍历 先打印根.
System.out.print(root.val+" ");
//再处理左子树.
preOrder(root.left);
//最后处理右子树.
preOrder(root.right);
}
//中序遍历: 左 根 右
public void inOrder(TreeNode root) {
if (root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
//后序遍历: 左 右 根
public void postOrder(TreeNode root) {
if(root == null) return;
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+" ");
}画图理解前序遍历的递归过程.

A的右子树递归过程与上图类似.
2. 层序遍历

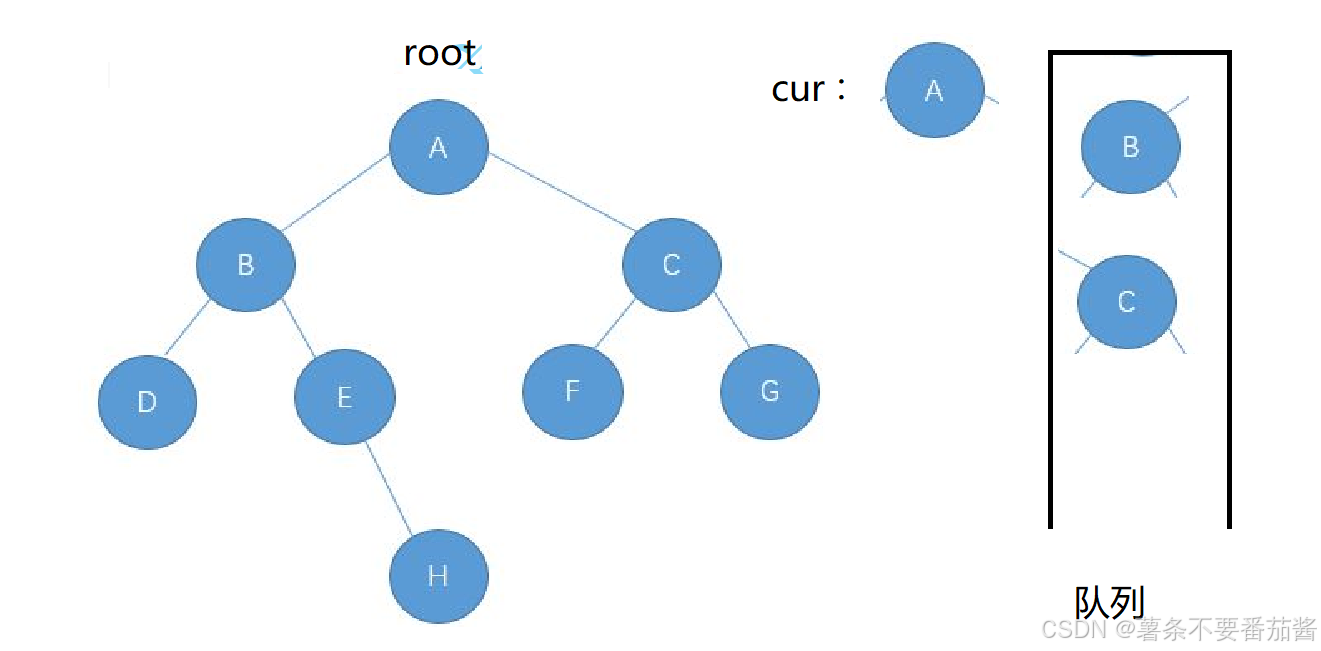
//二叉树的层序遍历
public void levelOrder1(TreeNode root) {
if(root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val+" ");
if(cur.left != null) {
queue.offer(cur.left);
}
if(cur.right != null) {
queue.offer(cur.right);
}
}
}1.5.3 二叉树的基本操作
public int size = 0;
//前序遍历,求二叉树节点个数
public void nodeSize(TreeNode root) {
if(root == null) return;
size++;
nodeSize(root.left);
nodeSize(root.right);
}
//中序和后序也类似, 无非就是把打印节点的代码换成size++;
第二种方法: 通过子问题解决: 总节点数 = 左子树 + 右子树 + 1;
思路: 总的节点数实际上就是所有的左节点数 + 右节点数 + 1.
public int nodeSize2(TreeNode root) {
if(root == null) return 0;
return nodeSize2(root.left) + nodeSize2(root.right) + 1;
}public int leafSize = 0;
public void gerLeafSize(TreeNode root) {
if(root == null) return;
if(root.left == null && root.right == null) {
leafSize++;
}
gerLeafSize(root.left);
gerLeafSize(root.right);
}public int getLeafSize2(TreeNode root) {
if(root == null) return 0;
if(root.left == null && root.right == null) {
return 1;
}
return getLeafSize2(root.left)+
getLeafSize2(root.right);
}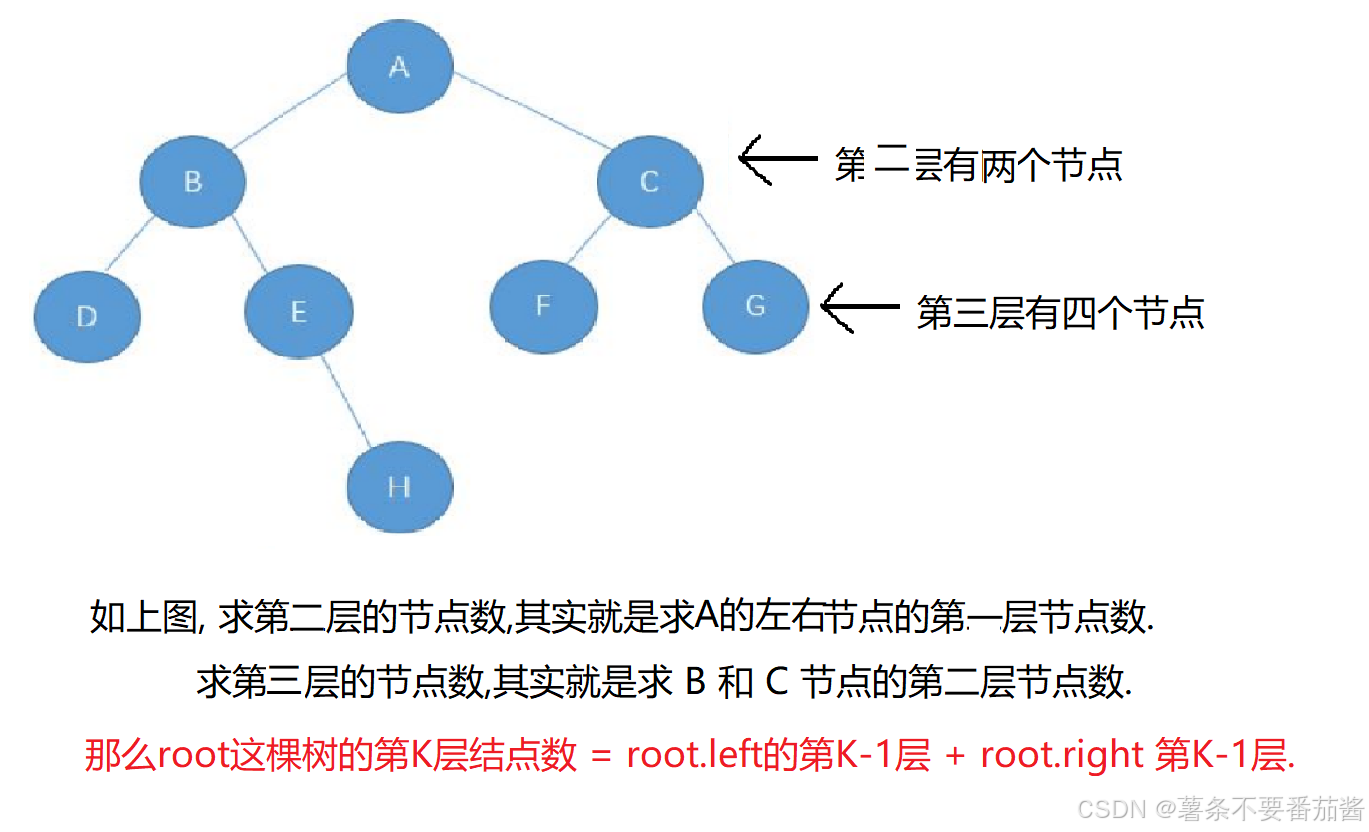
//获取第K层节点的个数
public int getKLeveNodeCount(TreeNode root,int k) {
if(root == null) return 0;
if(k == 1) {
return 1;
}
return getKLeveNodeCount(root.left,k-1) +
getKLeveNodeCount(root.right,k-1);
}//求二叉树的高度.
public int gerHeight(TreeNode root) {
if(root == null) return 0;
if(root.left == null && root.right == null) {
return 1;
}
int leftTree = gerHeight(root.left);
int rightTree = gerHeight(root.right);
return (leftTree > rightTree ? leftTree+1 : rightTree+1);
}//检测值为val的元素是否存在
public boolean find(TreeNode root,char key) {
if(root == null) return false;
if(root.val == key) {
return true;
}
boolean leftVal = find(root.left,key);
if(leftVal == true) {
return true;
}
boolean rightVal = find(root.right,key);
if(rightVal == true) {
return true;
}
return false;
}//判断一棵树是不是完全二叉树
public boolean isCompleteTree(TreeNode root) {
if(root == null) {
return true;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
if(cur != null) {
queue.offer(cur.left);
queue.offer(cur.right);
}else {
//遇到null节点了,跳出循环
break;
}
}
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
if(cur != null) {
//如果null之后存在不为空的节点,说明不是完全二叉树.
return false;
}
}
return true;
}原文地址:https://blog.csdn.net/2302_81886858/article/details/143601871
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
