强化学习Reinforcement Learning|Q-Learning|SARSA|DQN以及改进算法
一、强化学习RL
强化学习是机器学习的一个重要的分支,是一种有效的工具,在文献中被广泛用于解决MDP问题。在一个强化学习过程中,一个智能体只能通过和它所处的环境互动学习最优策略。特别地,智能体首先观察自己当前的状态,然后采取行动,并在获得新状态的同时获得即时的奖励。观察信息,即时的奖励和新的状态被用于去调整智能体的策略,这个过程将不断重复,直到智能体的策略接近最优策略。在强化学习中,Q-Learning是最有效的方法并且被文献中广泛使用。
二、Q-Learning算法(model-free, off-policy)
1、描述
在一个MDP模型中,我们想要获得最优的策略,对于智能体去最大化系统的预期长期奖励函数。因此,我们先定义状态值函数
,表示在每个状态s下遵循策略
所得到的期望值。策略
的值函数V通过无界限和折现MDP量化策略的优良性,可以表示为:

因为我们的目的是找到最优的策略,在每个状态的一个最优的动作可以被找到通过最优的状态值函数
.
如果我们用表示为所有状态动作对的最优的Q函数,然后最优的值函数可以被写为
.现在,问题被简化为寻找Q函数的最优值,即
.
1.1值函数的更新
对于所有的状态-动作对,可以通过迭代(iteration)的过程完成。具体来说,Q值的更新按照以下的规则更新:
.
对于上式中的Q值更新公式来说, 更新的思路主要就是新的Q值 = 旧的Q值 + 更新步长 * (实际Q值或目标Q值 - 估计Q值), 至于这里为什么用作为实际的Q值呢(对于未来的discounted reward中的action使用a'表示的是下一时刻的动作,与s'配套使用均表示下一时刻的s和a), 主要是因为在当前决策时间步 t ,
是由agent与env交互产生的即时reward, 然后再加上未来的discounted reward作为实际的Q值, 而
则表示在当前时间步t更新之前的Q值, 其可能为0, 也可能为非0, 若未更新过则为0, 但更新过则不一定为0.
1.2离线策略
对于离线策略的概念/定义主要为:在学习的过程中, agent不需要直接与env交互来更新其策略或价值函数. 那么对于Q-Learning算法的离线性主要可以从以下两个方面来分析:
a.经验回放Experience replay
即使在Q-Learning算法中未明确引入经验回放机制, 但是使用的Q-Table与Experience replay的目的几乎一样, 用于存储经验. agent将交互过程中的Q值保存下来, 然后可以通过过去的经验来更新其Q值, 从而提高学习的稳定性以及效率.
b.行为策略(a)与学习策略(update Q-value)相分离
主要是由于, 在Q-Learning算法中, 选择动作a的策略可能是贪心策略, 然而在更新Q值时, 使用的Q值并不一定会是动作a对应的Q-value. 需要保证当前s对应的多个a的state-action的最大Q-value.
2、算法

入门强化学习的同学就会知道,Q-Learning算法的state-action可以看成是一个键值对,实际上在这个算法中的Q值是利用表格存储起来的,可以称为Q-Table.对应的横轴和纵轴分别为state和action(实际的横纵究竟是state还是action无所谓,一般地,以横轴为action,纵轴为state).
这个更新背后的核心思想就是找到实际的Q值和它的估计值
的时间差(简称TD). 也就是这样,每次在使用TD方法计算TD-error也就是目标与预测间的误差时,我们需要在learn函数中传入的参数主要有
即可,在上述公式中的
获取Q表格中的对应的横坐标为
的这一行所有的state-action键值对对应的最大Q值即可;相反,下面要介绍的SARSA算法就需要在learn函数中传入参数
,因为Q-learning与SARSA算法在计算Q值的公式也不一样。只需要在(4)中,学习率
用于确定新的信息对现有Q值的影响。对于每次移动的步长也即学习速率可以选择固定的值,也可以在学习过程中动态调整. (这些都可以根据自己实际所设定)但是,为了保证Q-learning算法的收敛性,它必须满足假设1. 这里就不做过多的关于学习率也就是每次移动的步长做过多的解释.

一旦所有的Q值收敛或达到一定的迭代次数,那么算法将终止。然后这个算法产生最优的策略指示在每个状态下采取的行动,使得对状态空间中的所有状态都是最大的,即
.在步长假设下(即假设1),文献[19]证明了Q-learning算法收敛到最优动作值的概率为1.
值得注意的是,与状态值函数不同,Q函数是一种无模型(model-free)学习算法的例子,它不需要智能体事先知道系统模型参数,例如状态转移模型和奖励模型,来估计状态-动作值对。具体来说,Q函数的核心思想是通过与环境交互过程中获得的样本来近似状态动作对的值。此外,当值函数根据策略π获取所有动作的期望时,Q函数只关注特定状态下的特定动作。因此,使用q函数的学习算法比使用状态值函数的学习算法更简单。然而,从抽样的角度来看,q函数的维数比状态值函数的维数高,因此q函数可能更难获得足够的样本,即状态-动作对(state-action pairs)来学习。因此,如果系统模型是预先可用的,则通常优选状态值函数.
3、绘制reward折线图

总共训练50次,每一次会有多个回合, 回合的数量不是固定的, 然后把每个训练次数的所有回合获得的reward求平均作为当前训练次数的reward. 训练结束后, 我们可以明显看出的是, 在训练次数第1到20次时, reward在急剧上升, 然后在第30次之后reward逐渐收敛在0.1-0.15之间.
三、SARSA(State Action Reward State Action)算法
1、描述
SARSA是一种基于时序差分TD的在线Q-learning算法,尽管Q-learning算法可以在不需要了解环境的情况下为智能体找到最优的策略,但该算法以离线的方式工作(offline)。特别是算法1只有在所有的Q值收敛后才能得到最优策略。因此,本节提出了另一种在线(online)学习算法,即SARSA算法,它允许代理/智能体以在线方式接近最优策略。
与Q-learning算法不同,SARSA算法是一种在线算法,它允许智能体在每个决策步实时选择最优动作,而无需等待算法收敛。在Q-learning算法中,无论应用哪种策略,策略都是根据可用操作的最大奖励来更新的,即off-policy方法。相比之下,SARSA算法与环境交互,并直接从所采取的动作action(即策略上的方法)更新策略。注意SARSA算法从五元组Q(s, a, r, s', a')更新Q值, sarsa算法的Q值更新如下:
.
注意, 这里使用等号和向左箭头都可以, 相当于编程语言里面的赋值运算, 将右面式子的值赋给等式左面.
2、算法
初始化 Q(s,a) 对所有状态s和动作a
for episode in episodes:
s = env.reset()
a = RL.choose_action(s)
while not terminal_state:
a = ε-greedy探索(根据当前Q值表)
s_, r, done = env.step(a)
a_ = ε-greedy探索(针对下一个状态s_)
new_Q = Q(s,a) + α * (r + γ * Q(s_, a_) - Q(s,a))
update Q(s,a) with new_Q
s = s_
a = a_
# 注意, 在伪代码这里, s_和a_分别表示下一时刻的状态state以及动作action3、绘制reward折线图

4、Q-learning与SARSA的区别
上面分别讲解了Q-Learning算法与SARSA算法, 那么下面以一个具体的实际例子理解一下Q-Learning与SARSA算法的本质区别:

问题描述:如上图所示, 我们定义状态空间S=(s1,s2), 动作空间A=(a1,a2). 其中s1表示正在写作业的状态, s2表示继续写作业的状态; a1表示看电视动作,a2表示写作业的动作.
方面一:若当前正处于s1状态, 那么对于Q-learning算法可能会有:找到到达s2状态所对应的最大状态动作值函数Q(s1,a2)对应的动作a2, 但实际在做决策是可能不一定会选择能带来最大未来累计回报的动作a2. 相反, 对于SARSA算法就会有agent在评估未来discounted reward时, 会直接采用a的Q值评估, 而在实际采取动作时也会执行动作a. 这样也就是说明sarsa算法评估state-action值函数使用的动作就是实际执行的动作(可以看成是说到做到); 相反, Q-learning算法评估时会选择最大的state-action值函数的动作a进行评估, 但是在实际执行动作时却并不一定会选择动作a(可看成是非实践派).

方面二:如图所示, 使用Q-learning算法的agent“勇敢”, 因为Q-learning算法总是会选择最近的一条通往目的地的路, 不管这条路会有多么危险; 相反, 对于SARSA算法, 相对会保守一些, agent会选择距离危险远的, 到目的地是次要的, 需要保证自己存活下去, 这也是这两个算法的另一个不同之处. 在实际应用时, 需要考虑他们不同的特点进而选择合适的算法.
5、SARSA(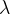 ):加入eligibility trace(资格迹)
):加入eligibility trace(资格迹)

上面我们已经了解了Sarsa算法, 那么下面我们开始介绍Sarsa(lammbda)算法. 本质上Sarsa算法是一种单步更新的算法, 即使用TD更新值函数, 在env中每走一步, 就更新一次自己的行为准则, 且可将单步更新的Sarsa算法表述为Sarsa(0). 若走完当前一步后, 又走了一步, 我们可以叫它为Sarsa(1). 同理, 那么我们选择在等待回合完毕, 然后一次性更新值函数等呢, 就可以称为Sarsa(lambda), 这样, 我们就可以等待回合完毕一次性更新. 下面, 着重介绍一下为什么要引入lambda?
5.1、资格迹的定义
资格迹E(s, a)用于跟踪状态-动作对的“资格”,即它们在当前回合中被访问的频率, 用于表示这个state-action对在当前时间步的重要性. 它为最近的状态-动作对赋予更高的权重,使得这些对在学习过程中更重要. 1、这种机制使得我们能够在获得奖励时,快速更新之前的 Q 值,从而加速学习过程. 2、通过结合 TD 误差和资格迹,更新 Q 表格的过程变得更加平滑和稳定。资格迹的引入减少了对单一状态-动作对的过度调整,帮助算法在学习过程中保持稳定性. 3、资格迹允许算法在学习过程中有效利用历史信息. 当智能体在某个状态采取了动作并获得奖励时,资格迹会使得与该状态-动作对相关的 Q 值得到更新,而不仅仅是当前状态-动作对. 这使得智能体能够更好地处理延迟奖励的问题.
5.2、资格迹类型
5.2.1累计资格迹
主要思路就是当agent访问到某个state-action对时, 其对应的资格迹增加. 这种方法强调了最近的访问, 并且在每次访问时都会累计资格, 资格变化如下:
.
5.2.2替代资格迹
主要思路就是说当agent访问某个状态-动作对时, 该对的资格迹会被重置为1, 而其他状态动作对的资格迹则会保持不变, 如下:
.
5.2.3总结
下面,对上述的资格迹做一个总结, 资格迹的值会随着时间的推移而衰减,允许agent在学习时考虑过去的状态-动作对。也就是SARSA()算法,资格轨迹是由Q-Table复制而来的,因此在对其做处理时,主要包括两种方法(5.2.1和5.2.2介绍的两种方法),分别为
# Method 1:意味着每一次访问该状态动作对state - action时,资格轨迹都会增加.
# self.eligibility_trace.loc[s, a] += 1
# Method 2:以当前状态s为基准的资格迹会被重置为 0,仅在当前状态 s 和动作 a 的位置上设置为 1。这意味着只有当前的状态-动作对在资格迹中被考虑。
self.eligibility_trace.loc[s, :] *= 0
self.eligibility_trace.loc[s, a] = 1
然后在更新完资格迹之后, 还要更新Q表格和资格迹的衰减
# 更新Q-tables, 将资格迹 * 学习率 * td-error将当前获取到的奖励信息传播到之前的state-action上
self.q_table += self.lr * error * self.eligibility_trace
# 衰减
self.eligibility_trace *= self.gamma * self.lambda_
5.1算法
下面描述一下算法的伪代码
初始化Q(s,a)对于所有的状态s,动作a.
for episode in episodes:
E(s,a)=0 对于所有的s,a
s = env.reset()
a = RL.choose_action(s) # 初始化每轮的状态和动作(贪心策略的选择action)
while not terminal_state:
s_,r,done = env.step(a)
a_ = RL.choose_action(s_) # 基于贪心策略选择下一时刻的动作action_
计算误差 error = r + gamma * Q(s',a') - Q(s,a)
对于所有的状态s和动作a的Q值以及资格迹E更新:
Q(s,a) = Q(s,a) + alpha * error * E(s,a)
E(s,a) = gamma * lambda * E(s,a)
s = s_
a = a_
5.2绘制reward折线图

四、Deep Q-Learning算法
1、简介
当状态空间和动作空间都很小时,Q-learning算法可以有效地获得最优策略。然而,在实践中,对于复杂的系统模型,这些空间通常很大。因此,Q-learning算法可能无法找到最优策略。因此,引入Deep Q -Learning(DQL)算法来克服这一缺点。直观地说,DQL算法实现了一个Deep Q-Network(DQN),即DNN,而不是Q表来推导出Q∗(s, a)的近似值,如图4(c)所示。

如[21]所述,当使用非线性函数逼近器时,强化学习算法获得的平均奖励可能不稳定甚至发散。这源于这样一个事实,即q值的微小变化可能极大地影响策略(即当Q值发生变化时,agent会选择不同的action,从而改变其行为策略)。因此,数据分布和Q值与目标值R + γ maxa Q(s',a')之间的相关性是变化的(即在训练过程中,数据的分布会随着agent的策略而变化,这种策略的变化会导致收集到的experience/transition在统计特性上有所不同)。为了解决这个问题,可以使用两种机制,即经验重放和目标Q-network.
- 经验回放机制(Experience replay mechanism):该算法首先初始化一个重放内存D,即内存池,其中转换(st, at, rt, st+1),即经验,随机生成,例如通过使用
(贪心)策略。然后,算法随机从D中选择转换的样本(即minibatch小批量)来训练DNN。训练后的DNN获得的q值将用于获得新的经验,即转换,然后这些经验将存储在内存池D中。这种机制允许DNN通过同时使用新旧经验来更有效地训练。此外,通过使用经验重放,转换更加独立和均匀分布,从而可以消除观测值之间的相关性。
简而言之,就是说有一个回放缓存的地方,将每次与环境交互所生成的transition(st, at, rt, st+1)都保存在缓存中,随后每一次都采用小批量样本数据训练智能体,这样用于训练的数据可能包含之前的也可能包含新生成的数据,不但会使得训练更高效,还会增加数据的多样性,进一步会导致降低训练过程中的过拟合问题。
- 固定目标Q网络(Fixed target Q-network):在训练过程中,q值会发生偏移。因此,如果使用一组不断变化的值来更新Q-network,则值估计可能会失控。这导致了算法的不稳定性。为了解决这个问题,使用目标Q-network来频繁但缓慢地更新主Q-networks的值(也就是网络的参数在每隔一定步数后才能成为著网络的参数)。这样可以显著降低目标和估计q值之间的相关性,从而稳定算法。
简而言之,就是会采用两个Q网络,原本的网络成为Q-network,用于估计Q值;又新增加了一个Q网络,称为Q-target网络,Q-target并不会自己更新,而是采用超参数N,每走N轮之后,就会将Q-network的网络参数复制给Q-target,这样也就是一小段轮次的样本会对应同一个训练目标。
举一个简单的例子,把训练神经网络比喻为射击游戏,如果Q-target每次都移动的话,那就相当于打移动靶子,每射击一次靶子就会移动一次,相比于打固定的靶子,无疑增加了训练的难度。相反,增加了Q-target之后,就相当于每隔一定时间靶子动一次,在这段时间范围内射击靶子都不会动,这样无疑会提高射击的稳定性。
2、算法描述

上述即为使用TD编写的DQN算法伪代码,在最基本的DQL算法中加入了经验回放缓存以及固定目标网络的机制,极大的提高了算法的性能,这里要注意,在实际写代码时,一定要注意好把估计Q值的网络参数复制给目标网络,若未加,对于网络的稳定性确实有很大的影响。(亲身经历)
3、改进部分
首先,我要阐述一点,就是说,我们学习改进部分要知道为什么要改进,以及改进后相比原来有什么特点(优点和缺点)。
1、Double Deep Q-Learning(双深度Q-learning)
第一种方法
在一些随机环境中,由于对动作值的过高估计,Q-learning算法表现不佳。这些高估是由引入的正偏差造成的,因为Q-learning使用最大动作值作为最大预期动作值的近似值,如Eq.(4)所示。主要的原因就是相同的样本被用来决定哪个动作是最好的,即期望回报最高,并且同样的样本又被用于估计状态-动作值(state-action value)。因此为了克服Q-learning算法的过估计问题,作者引入了一个方法,使用两个Q值函数Q1和Q2,去同时选择并且估计状态动作值。
特别是,动作的选择仍然取决于在线权重(online),这意味着就像Q-learning学习一样,我们仍然根据当前的值估计贪心策略的值,即
。然而第二组权重
用于公平的评估该策略的价值。第二组权重可以通过交换
和
的角色来对称的更新。受此思想的启发,[25]中的作者随后使用双深度Q-Network (DDQN)开发了双深度Q-Learning (DDQL)模型[26],其损失函数更新如下:

与Double Q-learning不同的是,将第二个网络的权值θ2替换为目标网络的权值θ'来评估当前贪心策略,如Eq.(8)所示。从DQN开始,对目标网络的更新保持不变,并且保持在线网络的周期性副本。由于DDQL的有效性,最近引入了DDQL的一些应用,以解决多通道无线网络中的动态频谱接入问题[27]和异构网络中的资源分配问题[28]。
综上,简单总结一下本方法的思路,其实就是又增加了一个网络称为Target Network,原本的Q-network用于寻找最大Q值对应的贪心策略的动作action,然后再使用Target Network估计这一时刻t下的st,at所对应的正确的Q值,这样的话,即使原本Q值被估计了,也不一定会在Target Network中有最大的Q值,可以有效地避免Q值过估计的情况,目标Q值的公式如下:
.
第二种方法
首先,也是采用两个Q-network,起到互相监督的作用,但这是两个异构的网络,由于它们之间的网络参数有所不同,那么对于同一个动作的评估也会有做不同。我们选取评估出来的较小值来计算目标,这样就能避免一个网络出现的Q值过高的情况发生了,公式如下,
.
2、Deep Q-Learning With Prioritized Experience Replay (优先级经验回放)
经验重放机制允许强化学习的智能体记住和重用经验,即从过去的转换(transition)。特别是,从重放存储器D中均匀地采样转换(transition)。然而,这种方法只是以与代理最初经历的相同频率重播转换,而不管它们的重要性如何。
因此,[29]的作者开发了一个优先考虑经验的框架,以便更频繁地重播重要的转换,从而更有效地学习。理想情况下,我们希望更频繁地对那些可以从中学习到很多东西的转换进行采样(Sample)。一般来说,具有优先经验重放(Prioritized Experience Replay,PER)的DQL以与最后遇到的绝对误差(absolute error)相关的概率对转换进行采样[29]。新的转换以最高优先级插入重放缓冲区,提供对最近转换的偏好。请注意,随机过渡也可能受到青睐,即使对它们知之甚少。通过对许多Atari游戏的实际实验,作者证明了在49个游戏中有41个游戏中,使用PER的DQL优于使用统一重播的DQL。然而,只有当我们能够在重放内存D中找到并定义重要经验(experience)时,才适合执行此解决方案。
3、 Dueling Deep Q-Learning(决斗深度Q-learning)
Q-learning算法(即算法1)中使用的Q值,即Q(s, a),表示在给定状态下采取某种行动的效果。一个动作在给定状态下的值实际上可以分解为两个基本值。第一个值是状态值函数,即V (s),用于估计处于特定状态s的重要性。第二个值是动作值函数,即A(a),用于估计选择一个动作a与其他动作相比的重要性。因此,Q值函数可以用两个基本值函数表示为:Q(s, a) = V (s) + A(a).
由于在许多的MDPs中,没有必要同时估计两个值,即Q函数Q(s,a)的动作值和状态值。例如,在许多赛车游戏中当且仅当智能体遇到障碍或敌人时,向左向右移动才有意义。受此思想的启发,作者在[30]中引入了使用两个完全连通层的流,即两个序列,而不是使用具有完全连通层的单个序列来实现DQN的思想。这两个流的构造使得它们能够对动作和状态值函数的单独估计,即V(s)和A(a)。最后,这两个流被组合以生成单个输出Q(s,a),如下所示:
![]()
其中,和
分别为V(s;
)和A(s,a';
)的参数。这里,|A|代表的是动作空间的大小,即动作空间中包含的动作总数。然后以类似于(7)的方式推导损失函数。通过仿真,作者表明,所提出的决斗DQN在57个学习到的Atari游戏中,有50个的性能优于DDQN[26]。然而,[30]的仿真结果表明提出的决斗架构显然只对具有大动作空间(large action spaces)的MDPs有利。对于较小的状态空间,决斗DQL的性能甚至不如双DQL。
4、 Asynchronous Multi-Step Deep Q-Learning(异步多步深度Q-Learning)
大多数Q-learning方法(如DQL和决斗DQL)都依赖于经验回放方法。然而,这种方法有几个缺点。例如,每个实际的交互(interaction)会使用更多的内存(memory)和计算资源(computation resources),并且还需要离线策略学习算法,根据旧的策略生成的数据更新。 这限制了DQL的应用。因此,作者在[31]中引入了一种使用多个智能体并行训练DNN的方法。特别地,作者提出了一种同时利用多个智能体的异步梯度体面更新的训练过程。与训练与环境交互的单个智能体不同,多个智能体同时与各自版本的环境env交互。经过一定的时间步长timestep后,来自智能体agent的累积梯度更新应用于全局模型,即DNN。这些更新是异步的,没有锁。此外,为了权衡策略梯度中的偏差和方差,作者采用n步更新方法[1]来更新奖励函数。特别地,截断的n步奖励函数可以定义为![]() 。因此,每个智能体agent的替代损失将由以下公式得出:
。因此,每个智能体agent的替代损失将由以下公式得出:

针对1步Q-learning、1步SARSA、n步Q-learning等不同的强化学习方法,分析了所提出的异步多步学习DQL对训练速度和质量的影响。它们表明异步更新对策略和值更新具有稳定作用。此外,所提出的方法在雅达利游戏上的性能优于当前最先进的算法,而在单个多核CPU而不是GPU上训练的时间只有一半。因此,异步DQL的一些最新应用已经开发出来,用于解决无线系统中的切换控制问题[32]。
5、 Distributional Deep Q-Learning(分布式深度Q-Learning)
上述所有方法都使用Bellman方程来近似未来奖励的期望值。然而,如果环境本质上是随机的,并且未来的奖励遵循多模态分布,那么基于期望值选择行动可能不会导致最优结果。例如,我们知道一个数据包在无线网络中的预期传输时间是20分钟。然而,这个信息可能没有那么有意义,因为它可能在大多数时候高估了传输时间。例如,期望传输时间是根据正常传输(无碰撞)和干扰传输(有碰撞)计算的。虽然干扰传输很少发生,但是需要花费大量的时间。因此,在大多数情况下,对期望传输的估计被高估了。这使得估计对DQL算法没有用处。
因此,[33]中的作者引入了一种使用分布强化学习的解决方案,根据q值函数的分布而不是期望来更新q值函数。其中,设Z(s, a)为从状态s出发,执行动作a,遵循当前策略得到的返回,则Q(s, a) = E[Z(s, a)]。这里,Z代表未来奖励的分布,不再像q值那样是一个标量。得到Bellman方程的分布形式:Z(s, a) = r + γZ(s', a')。尽管所提出的分布式深度q学习被证明在许多雅达利2600游戏(57款游戏中的45款)上,它的性能优于传统的DQL[21],它的性能很大程度上依赖于分布函数Z。如果Z定义良好,那么分布式深度q学习的性能比DQL的性能要重要得多。否则,它的性能甚至比DQL还差。
6、 Deep Q-Learning With Noisy Nets(基于噪声网络的深度Q-learning)
在[34]中,作者介绍了Noisy Net,这是一种神经网络,其偏差和权重在训练过程中通过噪声的参数函数进行迭代扰动。这个网络基本上是将高斯噪声添加到网络的最后一层(全连接的,fully-connected)。该噪声的参数可以在训练过程中由模型调整,这允许智能体决定何时以及以何种比例将不确定性引入其权重。特别地,为了实现有噪声网络,我们首先用随机化的动作值函数代替γ-贪心策略。然后,将值网络的全连通层参数化为一个噪声网络,其中参数取自每重放一步后的噪声网络参数分布。对于重放,当前有噪声的网络参数样本在批处理中保持固定。由于DQL对每个动作步骤都进行一步优化,因此在每个动作之前都会对噪声网络参数进行重新采样。
通过实验结果,作者证明,通过在DNN中加入高斯噪声层,传统DQL[21]、dueling DQL[30]和异步DQL[31]的性能可以显著提高,适用于广泛的Atari游戏。然而,噪声对深度DQL算法性能的影响在文献中仍存在争议,因此分析噪声层的影响需要进一步研究。
7、Rainbow Deep Q-Learning(彩虹深度Q-learning)
在[35]中,作者提出了一种解决方案,将上述七种解决方案(包括DQL)的所有优点集成到一个学习代理中,称为Rainbow DQL。特别是,该算法首先定义了基于异步多步分布式DQL的损失函数。然后,作者将多步分布损失与双q学习结合起来,利用根据q网络选择的st+n中的贪心行为作为自举行为a * t+n,并利用目标网络对其进行评估。
在标准的比例优先重放[29]技术中,使用绝对td误差来确定转换的优先级。这里,时隙的td误差是在该时隙估计的误差。然而,在提出的Rainbow DQL算法中,所有分布式Rainbow变体都通过Kullbeck-Leibler (KL)损失对转换进行优先级排序,因为这种损失可能对有噪声的随机环境更具鲁棒性。或者,dnn的决斗架构在[30]中提出。最后,为了减少独立噪声变量的数量,使用noisenet层[35]替换所有线性层。通过仿真,作者证明了这是最先进的技术,在57个Atari 2600游戏中,它比文献中几乎所有当前的DQL算法都要好。
References
[1]paper:https://arxiv.org/abs/1602.01783.
[2]莫凡Python.
原文地址:https://blog.csdn.net/m0_64578069/article/details/140471361
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
