强化学习的数学原理-09策略梯度
文章目录
Basic idea of policy gradient
截至目前,所有的策略policy都是用表格表示的,如下图所示,每个状态对应一行动作。
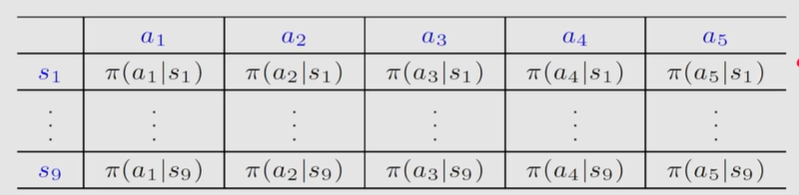
现在由于策略梯度的方法是直接建立一个关于策略的函数,于是就要改变策略的形式。
现在需要引入一个参数 θ \theta θ,那么策略表示为一个关于参数的函数。
π ( a ∣ s , θ ) , w h e r e θ ∈ R m i s a p a r a m e t e r v e c t o r \pi(a \mid s,\theta), \quad where \; \theta \in \mathbb{R}^{m} \; is \; a \; parameter \; vector π(a∣s,θ),whereθ∈Rmisaparametervector
- 目前这个策略函数最广泛的形式就是神经网络,神经网络的输入是
s
t
a
t
e
state \;
state输出是采用每个动作的概率,参数是
θ
\theta
θ
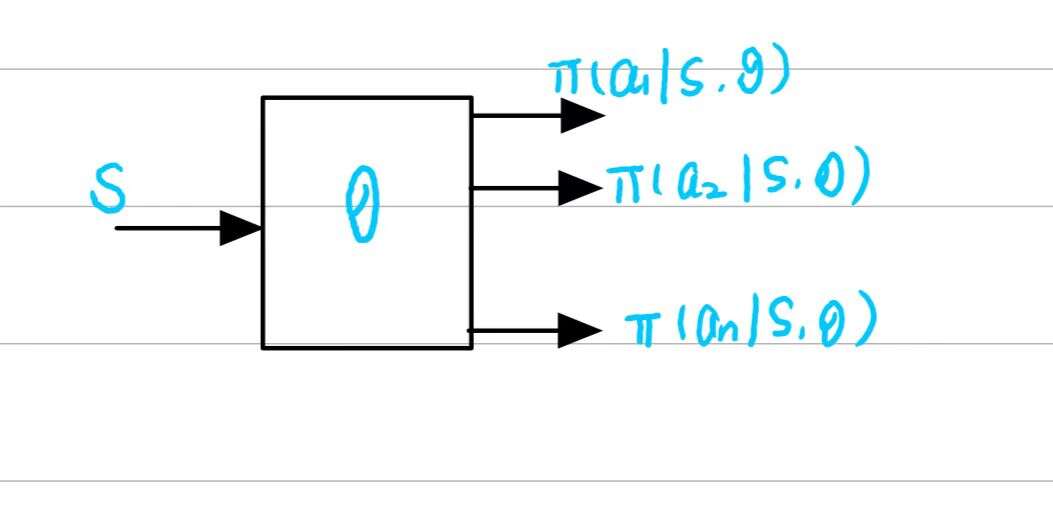
- 引入函数的优点和之前的 v a l u e f u n c t i o n a p p r o x i m a t i o n value \; function \; approximation valuefunctionapproximation是类似的,一方面是存储上 f u n c t i o n function function能在 s t a t e s p a c e 、 a c t i o n s p a c e state \; space 、action \;space statespace、actionspace很大的时候节省很多空间,另一方面就是泛化能力会得到提升,主要是在 s t o r a g e 和 g e n e r a l i z a t i o n storage和generalization storage和generalization两方面有较大的优点。
表格形式和函数形式上对于策略的几点区别
- 定义最优策略:表格形式最优策略定义是最优策略下的 s t a t e v a l u e state \; value statevalue大于其他所有策略的,而函数形式下的最优策略引入了一个 s c a l a r m e t r i c s scalar \; metrics scalarmetrics来衡量什么是最优策略
- 获取在s状态下,采取action的概率:表格形式直接查表即可,而函数形式需要通过神经网络进行一次推理得到。
- 改变策略:表格形式直接索引然后改变,函数形式通过改变参数 θ \theta θ来改变策略
下面就看一下 p o l i c y g r a d i e n t policy \; gradient policygradient最基本的思想
- 首先需要一个 m e t r i c s metrics metrics或者 o b j e c t i v e f u n c t i o n objective \; function objectivefunction去定义最优策略 J ( θ ) J(\theta) J(θ)
- 有了目标函数之后就可用梯度的算法做优化,去寻找最优策略 θ t + 1 = θ t + α ∇ θ J ( θ t ) \theta_{t+1}=\theta_{t}+\alpha \nabla_{\theta}J(\theta_t) θt+1=θt+α∇θJ(θt)
这就是策略梯度的思想,这个想法是很简单的,但是这其中会存在一些问题。
- 怎么选取目标函数
- 怎么去计算梯度?
Metrics to define optimal policies
主要有两大类 m e t r i c s metrics metrics
average value
第一种: a v e r a g e s t a t e v a l u e average \; state \; value averagestatevalue或者被叫做 a v e r a g e v a l u e average \; value averagevalue,于是就可以定义 m e t r i c s metrics metrics
v π ˉ = ∑ s ∈ S d ( s ) v π ( s ) \bar{v_{\pi}}=\sum_{s \in S}d(s)v_{\pi}(s) vπˉ=s∈S∑d(s)vπ(s)
v π ˉ \bar{v_{\pi}} vπˉ是策略的函数,不同策略对应的值不同,所以就可以去优化,找到一个最优的策略让这个值达到最大。
- v π ˉ \bar{v_{\pi}} vπˉ实际上是一个 s t a t e v a l u e state \; value statevalue的加权平均
- d ( s ) ≥ 0 d(s) \ge 0 d(s)≥0是每个状态的权重
- 因为 ∑ s ∈ S d ( s ) = 1 \sum_{s \in S}d(s)=1 ∑s∈Sd(s)=1,我们可以把 d ( s ) d(s) d(s)描述为概率分布。那么刚才的 m e t r i c s metrics metrics就可以写成这个形式 v π ˉ = E [ v π ( S ) ] , S \bar{v_{\pi}}=\mathbb{E}[v_{\pi}(S)],S vπˉ=E[vπ(S)],S表示随机变量 S ∼ d S \sim d S∼d
上面相乘再相加的形式可以写成一种更简洁的形式就是两个向量的内积
v π ˉ = ∑ s ∈ S d ( s ) v π ( s ) = d T v π \bar{v_{\pi}}=\sum_{s \in S}d(s)v_{\pi}(s)=d^Tv_{\pi} vπˉ=s∈S∑d(s)vπ(s)=dTvπ
v π = [ . . . , v π ( s ) , . . . ] T ∈ R S v_{\pi}=[...,v_{\pi}(s),...]^T\in \mathbb{R}^{\mathbb{S}} vπ=[...,vπ(s),...]T∈RS
d = [ . . . , d ( s ) , . . . ] T ∈ R S d=[...,d(s),...]^T\in \mathbb{R}^{\mathbb{S}} d=[...,d(s),...]T∈RS
上面就结束了第一种 m e t r i c metric metric总体思想,但是还有问题没有解决就是如何选择 d d d
d d d的选择也有两种情况,一种是 d d d是独立于 π \pi π的,另一种就是依赖于 π \pi π的
第一种情况是简单的.
v π ˉ = ∑ s ∈ S d ( s ) v π ( s ) = d T v π \bar{v_{\pi}}=\sum_{s \in S}d(s)v_{\pi}(s)=d^Tv_{\pi} vπˉ=s∈S∑d(s)vπ(s)=dTvπ
∇ v π ˉ = d T ∇ v π \nabla \bar{v_{\pi}} = d^T \nabla v_{\pi} ∇vπˉ=dT∇vπ
只需要对后面的 v π v_{\pi} vπ求梯度,为了表明 d d d和 π \pi π没有关系就把 d d d写成 d 0 d_0 d0, v π ˉ \bar{v_{\pi}} vπˉ就写成 v π 0 ˉ \bar{v_{\pi}^0} vπ0ˉ
d d d和 π \pi π没有关系那么如何选择 d d d呢?
- 最简单的就是把所有的状态认为是 e q u a l l y i m p o r t a n t equally \; important equallyimportant,所以 d 0 ( s ) = 1 ∣ S ∣ d_0(s)=\frac{1}{|S|} d0(s)=∣S∣1
- 如何我们关注某些特殊的状态,就可以给某些状态较大的 d d d
第二种情况就是和策略有关系
一种选择 d d d的方式是选择在 π \pi π策略下的 s t a t i o n a r y d i s t r i b u t i o n stationary \; distribution stationarydistribution
然后这个概率可以直接计算出来
d π T P π = d π T d^T_{\pi}P_{\pi}=d^T_{\pi} dπTPπ=dπT
P π P_{\pi} Pπ是状态转移概率矩阵
average reward
第二种就是 a v e r a g e o n e − s t e p r e w a r d average \; one-step \; reward averageone−stepreward
v π ˉ = ∑ s ∈ S d ( s ) r π ( s ) = E [ r π ( S ) ] \bar{v_{\pi}}=\sum_{s \in S}d(s)r_{\pi}(s)=\mathbb{E}[r_{\pi}(S)] vπˉ=s∈S∑d(s)rπ(s)=E[rπ(S)]
w h e r e S ∼ d π where \; S \sim d_{\pi} whereS∼dπ
r π ( s ) = ∑ a ∈ A π ( s ∣ a ) r ( s , a ) r_{\pi}(s)=\sum_{a \in A}\pi(s|a)r(s,a) rπ(s)=a∈A∑π(s∣a)r(s,a)
r ( s , a ) = E [ R ∣ s , a ] = ∑ r r p ( r ∣ s , a ) r(s,a)=\mathbb{E}[R|s,a]=\sum_r rp(r|s,a) r(s,a)=E[R∣s,a]=r∑rp(r∣s,a)

这部分还有一点数学形式待完善…
Gradient of the metrics
计算梯度是 p o l i c y g r a d i e n t m e t h o d s policy \; gradient \; methods policygradientmethods最麻烦的部分
首先这里有很多不同的 m e t r i c s ( o b j e c t i v e f u n c t i o n ) v π ˉ 、 r π ˉ 、 v π 0 ˉ metrics(objective \; function) \; \bar{v_{\pi}}、\bar{r_{\pi}}、\bar{v^0_{\pi}} metrics(objectivefunction)vπˉ、rπˉ、vπ0ˉ
还需要区分 d i s c o u n t e d c a s e discounted \; case discountedcase和 u n d i s c o u n t e d c a s e undiscounted \; case undiscountedcase
这里只给出一个总结的情况
∇ θ J ( θ ) = ∑ s ∈ S η ( s ) ∑ a ∈ A ∇ θ π ( a ∣ s , θ ) q ( s , a ) \nabla_{\theta}J(\theta) = \sum_{s \in S} \eta(s) \sum_{a \in A}\nabla_{\theta}\pi(a|s,\theta)q(s,a) ∇θJ(θ)=s∈S∑η(s)a∈A∑∇θπ(a∣s,θ)q(s,a)

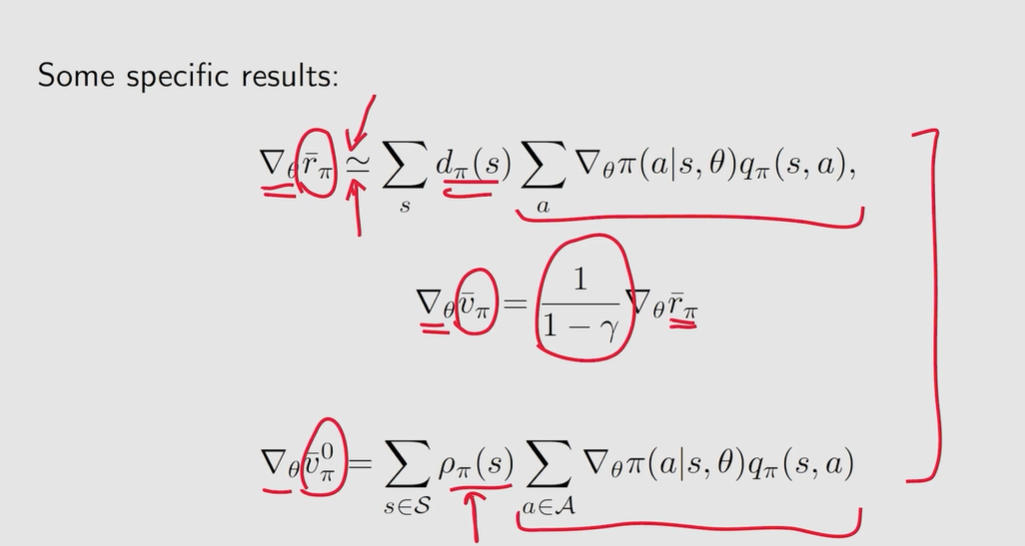
∇ θ J ( θ ) = ∑ s ∈ S η ( s ) ∑ a ∈ A ∇ θ π ( a ∣ s , θ ) q ( s , a ) = E [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] \begin{align}\nabla_{\theta}J(\theta) &= \sum_{s \in S} \eta(s) \sum_{a \in A}\nabla_{\theta}\pi(a|s,\theta)q(s,a) \\ &= \mathbb{E}[\nabla_{\theta} \ln\pi(A|S,\theta)q_{\pi}(S,A)] \end{align} ∇θJ(θ)=s∈S∑η(s)a∈A∑∇θπ(a∣s,θ)q(s,a)=E[∇θlnπ(A∣S,θ)qπ(S,A)]
w h e r e S ∼ η a n d A ∼ π ( A ∣ S , θ ) where \; S \sim \eta \; and \; A \sim \pi(A|S,\theta) whereS∼ηandA∼π(A∣S,θ)
上面这个式子是有用的,因为有期望,所以可以通过采样的方式去近似。这个就是 s t o c h a s t i c g r a d i e n t d e s c e n t stochastic \; gradient \; descent stochasticgradientdescent的思路。
如何得到上面的等式呢?
∇ θ ln π ( a ∣ s , θ ) = ∇ θ π ( a ∣ s , θ ) π ( a ∣ s , θ ) \nabla_{\theta}\ln \pi(a|s,\theta) = \frac{\nabla_{\theta }\pi(a|s,\theta)}{\pi(a|s,\theta)} ∇θlnπ(a∣s,θ)=π(a∣s,θ)∇θπ(a∣s,θ)
上面这个式子实际就是复合函数求导的链式法则
然后把等式右边的分母乘到左边去
π ( a ∣ s , θ ) ∇ θ ln π ( a ∣ s , θ ) = ∇ θ π ( a ∣ s , θ ) {\pi(a|s,\theta)}\nabla_{\theta}\ln \pi(a|s,\theta) = {\nabla_{\theta }\pi(a|s,\theta)} π(a∣s,θ)∇θlnπ(a∣s,θ)=∇θπ(a∣s,θ)
把这个式子带入到
∇ θ J = ∑ s d ( s ) ∑ a ∇ θ π ( a ∣ s , θ ) q π ( s , a ) = ∑ s d ( s ) ∑ a π ( a ∣ s , θ ) ∇ θ ln π ( a ∣ s , θ ) q π ( s , a ) = E S ∼ d [ ∑ a π ( a ∣ S , θ ) ∇ θ ln π ( a ∣ S , θ ) q π ( S , a ) ] = E s ∼ d , A ∼ π [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] = E [ ∇ θ ln π ( A ∣ S , θ ) q π ( S , A ) ] \begin{align}\nabla_{\theta}J&=\sum_sd(s)\sum_a\nabla_{\theta}\pi(a|s,\theta)q_{\pi}(s,a)\\ &=\sum_sd(s)\sum_a\pi(a|s,\theta) \nabla_{\theta}\ln\pi(a|s,\theta)q_{\pi}(s,a) \\ &=\mathbb{E}_{S \sim d}[\sum_a\pi(a|S,\theta) \nabla_{\theta}\ln\pi(a|S,\theta)q_{\pi}(S,a)] \\ &= \mathbb{E}_{s \sim d, A \sim\pi} [\nabla_{\theta} \ln\pi(A|S,\theta)q_{\pi}(S,A)] \\ &= \mathbb{E} [\nabla_{\theta} \ln\pi(A|S,\theta)q_{\pi}(S,A)]\end{align} ∇θJ=s∑d(s)a∑∇θπ(a∣s,θ)qπ(s,a)=s∑d(s)a∑π(a∣s,θ)∇θlnπ(a∣s,θ)qπ(s,a)=ES∼d[a∑π(a∣S,θ)∇θlnπ(a∣S,θ)qπ(S,a)]=Es∼d,A∼π[∇θlnπ(A∣S,θ)qπ(S,A)]=E[∇θlnπ(A∣S,θ)qπ(S,A)]
分析一下上面的一些点
因为需要计算 ln π ( a ∣ s , θ ) \ln\pi(a|s,\theta) lnπ(a∣s,θ),所以必须确保对于所有 s , a , θ s,a,\theta s,a,θ
π ( a ∣ s , θ ) > 0 \pi(a|s,\theta) \mathbb{>} 0 π(a∣s,θ)>0
但是之前我们的 g r e a d y p o l i c y gready \; policy greadypolicy和其他的 d e m e s t i c p o l i c y demestic \; policy demesticpolicy出现过 π ( a ∣ s , θ ) = 0 \pi(a|s,\theta) \mathbb{=} 0 π(a∣s,θ)=0的一些情况如何去避免的,这里可以使用 s o f t m a x softmax softmax这个 f u n c t i o n function function去解决。
s o f t m a x f u n c t i o n softmax \; function softmaxfunction这个函数主要做的内容就是去归一化去把一个 ( − ∞ , + ∞ ) (-\infty, +\infty) (−∞,+∞)映射到 ( 0 , 1 ) (0,1) (0,1)

因为 π ( a ∣ s , θ ) > 0 \pi(a|s,\theta) \mathbb{>} 0 π(a∣s,θ)>0所以这个策略是 s t o c h a s t i c stochastic stochastic和 e x p l o r a t o r y exploratory exploratory的
Gradient-ascent algorithm(REINFORCE)
θ t + 1 = θ t + α ∇ θ J ( θ ) = θ t + α E [ ∇ θ ln π ( A ∣ S , θ t ) q π ( S , A ) ] \begin{align*} \theta_{t+1}&=\theta_t + \alpha \nabla_{\theta} J(\theta)\\ &= \theta_t + \alpha \mathbb{E}[\nabla_{\theta} \ln \pi(A|S, \theta_t)q_{\pi}(S,A)]\end{align*} θt+1=θt+α∇θJ(θ)=θt+αE[∇θlnπ(A∣S,θt)qπ(S,A)]
这个公式是没有办法应用的,因为公式中有期望,所以需要通过随机的梯度来代替真实梯度。
θ t + 1 = θ t + α ∇ θ ln π ( a t ∣ s t , θ t ) q π ( s t , a t ) \begin{align*} \theta_{t+1}&=\theta_t+\alpha \nabla_{\theta} \ln\pi(a_t|s_t,\theta_t)q_{\pi}(s_t,a_t) \end{align*} θt+1=θt+α∇θlnπ(at∣st,θt)qπ(st,at)
但是上面的式子仍然是无法应用的,因为上面的式子里面涉及了 q π ( s t , a t ) q_{\pi}(s_t,a_t) qπ(st,at)是真实的 a c t i o n v a l u e action \; value actionvalue
为了解决上面的问题,这里是对这个 q q q进行采样,用 q t ( s t , a t ) q_t(s_t,a_t) qt(st,at)来代替
关于怎么采样于是又有两种方法。
- 一种是 M o n t e − C a r l o b a s e d Monte-Carlo \; based Monte−Carlobased,被称为 R E I N F O R C E REINFORCE REINFORCE
- 还有就是其他算法,比如 T D TD TD,这就和后面 A c t o r − C r i t i c Actor-Critic Actor−Critic有关了
上面就是梯度上升算法,下面是一些关于其中细节的实操
E S ∼ d , A ∼ π [ ∇ θ ln π ( A ∣ S , θ t ) q π ( S , A ) ] → ∇ θ ln π ( a ∣ s , θ t ) q π ( s , a ) \mathbb{E}_{S \sim d, A \sim \pi}[\nabla_{\theta} \ln \pi(A|S, \theta_t)q_{\pi}(S,A)] \rightarrow \nabla_{\theta} \ln\pi(a|s,\theta_t)q_{\pi}(s,a) ES∼d,A∼π[∇θlnπ(A∣S,θt)qπ(S,A)]→∇θlnπ(a∣s,θt)qπ(s,a)
如何 s a m p l e S sample \; S sampleS
- S ∼ d S \sim d S∼d是 d d d在按策略 π \pi π下长期运行后得到的一个稳定的状态
如何 s a m p l e A sample \; A sampleA
- A ∼ π ( A ∣ S , θ ) A \sim \pi(A|S,\theta) A∼π(A∣S,θ)因此 a t s h o u l d b e s a m p l e d f o l l o w i n g π ( θ t ) a t s t a_t \; should \; be \; sampled \; following \; \pi(\theta_t) \; at \; s_t atshouldbesampledfollowingπ(θt)atst
- 所以 P G PG PG是 o n − p o l i c y on-policy on−policy的
如何从另一个角度去理解这个算法
因为
∇ θ ln π ( a t ∣ s t , θ t ) = ∇ θ π ( a t ∣ s t , θ t ) π ( a t ∣ s t , θ t ) \nabla_{\theta}\ln\pi(a_t|s_t,\theta_t)=\frac{\nabla_{\theta}\pi(a_t|s_t,\theta_{t})}{\pi(a_t|s_t,\theta_{t})} ∇θlnπ(at∣st,θt)=π(at∣st,θt)∇θπ(at∣st,θt)
因此上面的梯度上升算法可以重写为
θ t + 1 = θ t + α ∇ θ ln π ( a t ∣ s t , θ t ) q t ( s t , a t ) = θ t + α ( q t ( s t , a t ) π ( a t ∣ s t , θ t ) ) ∇ θ π ( a t ∣ s t , θ t ) \begin{align} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta}\ln_{\pi}(a_t|s_t,\theta_t)q_t(s_t,a_t) \\ &= \theta_t + \alpha (\frac{q_t(s_t, a_t)}{\pi(a_t|s_t,\theta_t)}) \nabla_{\theta}\pi(a_t|s_t,\theta_t)\end{align} θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)=θt+α(π(at∣st,θt)qt(st,at))∇θπ(at∣st,θt)
然后可以把$ \beta_t = (\frac{q_t(s_t, a_t)}{\pi(a_t|s_t,\theta_t)}) $
于是上面的式子就可以化为
θ t + 1 = θ t + α β t ∇ θ π ( a t ∣ s t , θ t ) \theta_{t+1} = \theta_t + \alpha \beta_t \nabla_{\theta} \pi(a_t|s_t,\theta_t) θt+1=θt+αβt∇θπ(at∣st,θt)
上面这个式子是在优化 π ( a t , s t ) \pi(a_t,s_t) π(at,st)的值通过改变 θ \theta θ

θ t + 1 = θ t + α ∇ θ ln π ( a t ∣ s t , θ t ) q π ( s t , a t ) \begin{align} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta}\ln_{\pi}(a_t|s_t,\theta_t)q_{\pi}(s_t,a_t) \\ \end{align} θt+1=θt+α∇θlnπ(at∣st,θt)qπ(st,at)
其 q q q通过采样的方法去替代真实的值
θ t + 1 = θ t + α ∇ θ ln π ( a t ∣ s t , θ t ) q t ( s t , a t ) \begin{align} \theta_{t+1} &= \theta_t + \alpha \nabla_{\theta}\ln_{\pi}(a_t|s_t,\theta_t)q_t(s_t,a_t) \\ \end{align} θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)
如何 q π ( s t , a t ) q_{\pi}(s_t,a_t) qπ(st,at)是通过蒙特卡洛方法得到的就把这个算法叫做 R E I N F O R C E REINFORCE REINFORCE
R E I N F O R C E REINFORCE REINFORCE的伪代码

原文地址:https://blog.csdn.net/weixin_61426225/article/details/143716239
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
