R语言数据分析案例39-合肥市AQI聚类和多元线性回归
一、研究背景
随着全球工业化和城市化的迅速发展，空气污染问题日益凸显，已成为影响人类健康和环境质量的重大挑战。空气污染不仅会引发呼吸系统、心血管系统等多种疾病，还会对生态系统造成不可逆转的损害。因此，空气质量的监测和治理成为各国政府和学术界关注的重点。
二、研究意义
研究合肥市空气质量指数（AQI）及其影响因素，不仅有助于理解空气污染的主要来源和变化趋势，还可以为政府制定有效的污染控制政策提供科学
依据。通过构建预测模型和进行实证分析，可以更准确地预估未来空气质量状况，从而采取预防性措施，减少污染物排放，提升城市居民的生活质量和健康水平。。。。。
三、实证分析
首先读取数据集展示数据前五行
aqi_data <- read.csv("合肥四月份AQI(1).csv")
head(aqi_data ,5)
# 检查数据结构
str(aqi_data)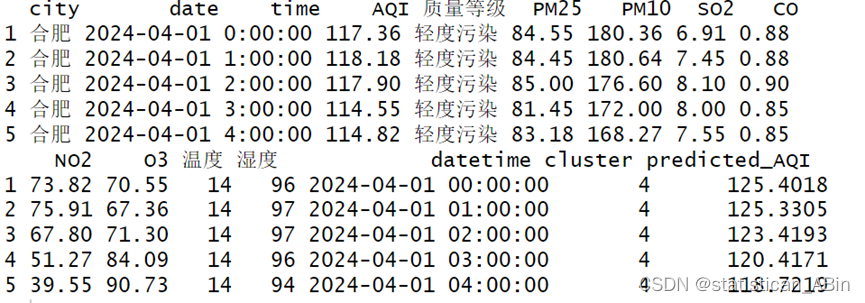
上面展示了2024年4月1日合肥市在不同时间段的空气质量指数（AQI）及其相关污染物浓度数据，包括PM2.5、PM10、SO2、CO、NO2、O3，以及气温和湿度。
随后检查数据结构
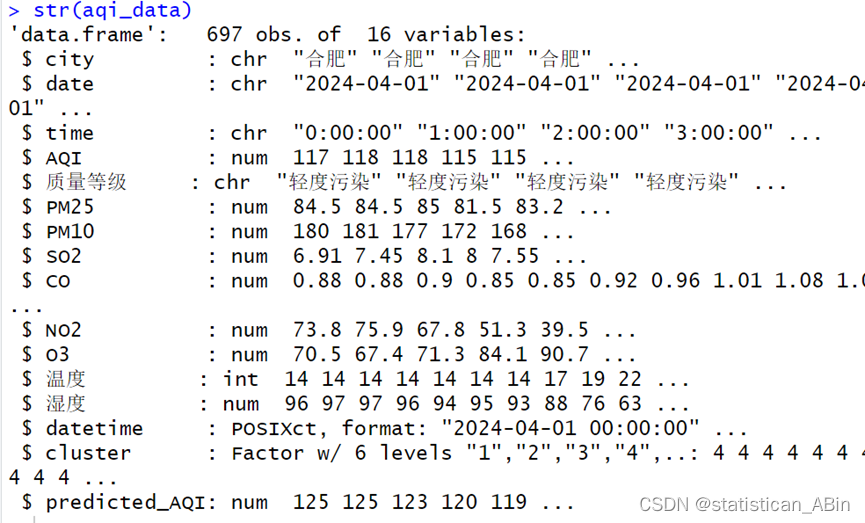
发现包括字符串和数值型数据
接下来检查缺失值，并预处理
结果不存在缺失值，继续进行分析
接下来对数据进行描述性统计
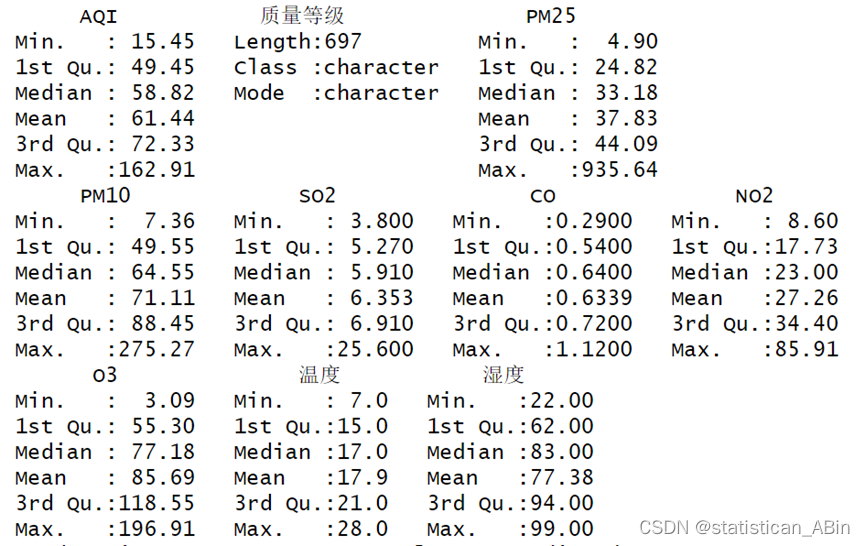
图展示了各污染物和气象因素的描述性统计分析结果，包括AQI、PM2.5、PM10、SO2、CO、NO2、O3的最小值、最大值、中位数、均值及四分位数等统计信息
接下来可视化数据集
# 绘制箱型图
ggplot(aqi_data, aes(x = city, y = AQI)) +
geom_boxplot() +
labs(title = "城市空气质量指数(AQI)箱型图", x = "城市", y = "AQI") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5))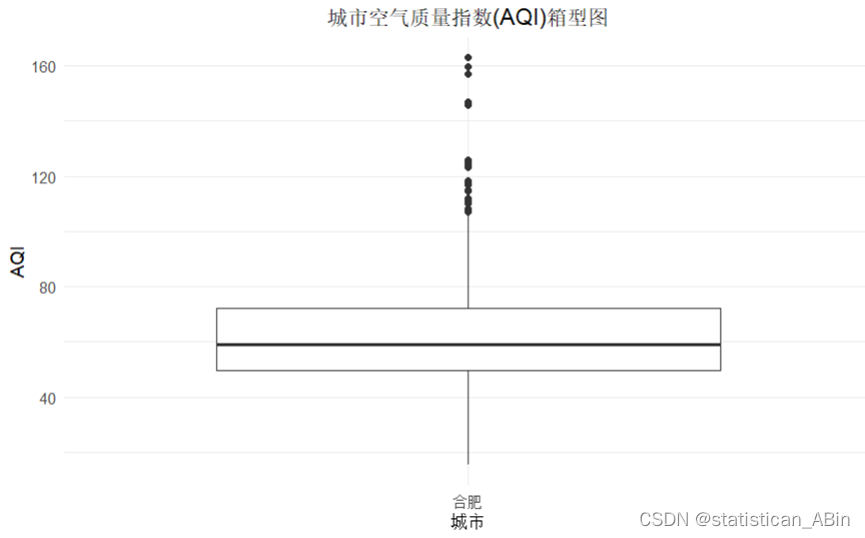 
该图展示了合肥市空气质量指数（AQI）的箱型图，直观地显示了AQI值的分布情况。箱型图中间的线表示中位数，图中显示AQI的中位数大约在60左右。。。
ggplot(aqi_data, aes(x = datetime, y = AQI)) +
geom_line(color = "blue") +
labs(title = "合肥四月份空气质量指数(AQI)变化", x = "时间", y = "AQI") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5))
该图展示了合肥市四月份空气质量指数（AQI）随时间的变化趋势。这是一张时间序列折线图，横轴表示时间，纵轴表示AQI值。图中显示，整个四月份AQI值波动明显，有多个高峰和低谷。
相关系数热力图
ggplot(melted_cor_matrix, aes(x = Var1, y = Var2, fill = value)) +
geom_tile(color = "white") +
scale_fill_gradient2(low = "blue", high = "red", mid = "white", midpoint = 0, limit = c(-1, 1), space = "Lab", name = "相关系数") +
labs(title = "空气质量相关系数热力图", x = "变量", y = "变量") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5))
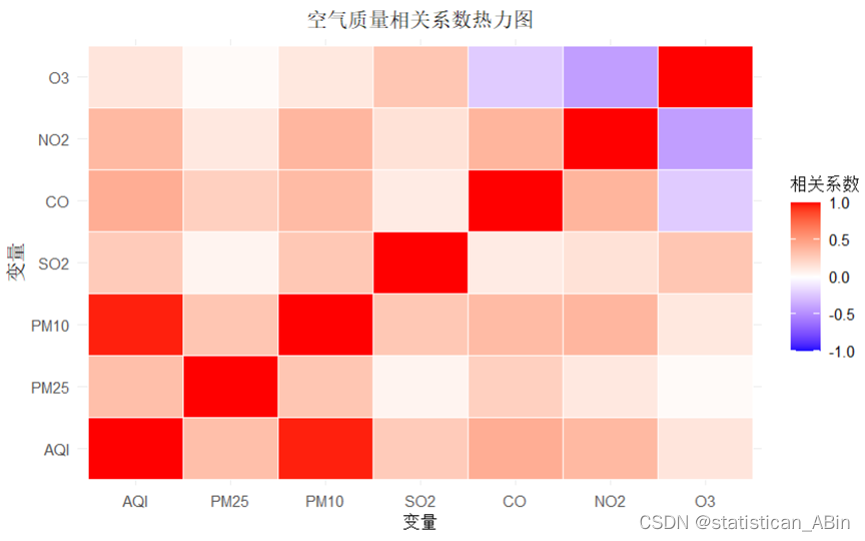热力图中，深红色表示高度正相关，深蓝色表示高度负相关，而浅色表示低相关或无关。图中显示，AQI与PM2.5和PM10的相关性最高，相关系数接近1，这表明颗粒物是影响空气质量的重要因素。。。
使用K-means聚类分析空气质量数据
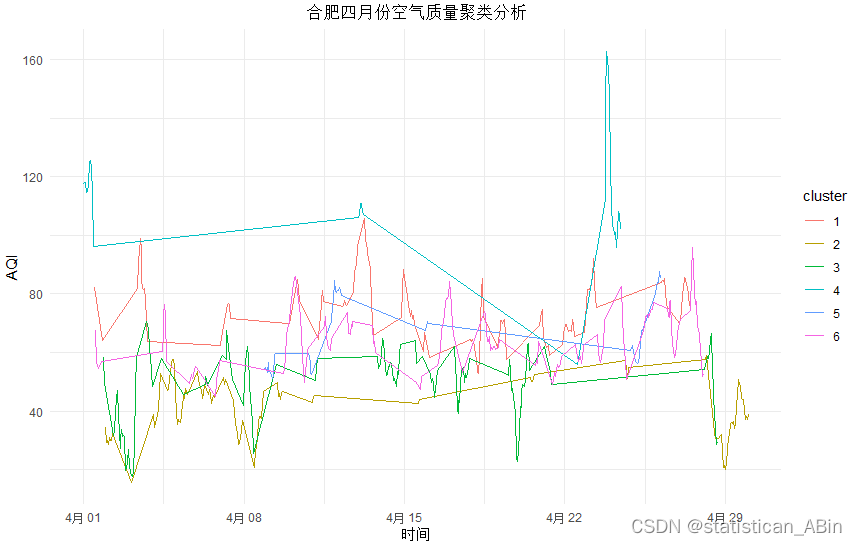
图展示了合肥市四月份空气质量的K-means聚类分析结果，通过不同颜色的线条表示不同聚类（cluster）的AQI变化趋势。图中显示，AQI数据被分为六个聚类，每个聚类代表了不同时间段内相似的AQI模式。可以看到。。。
构建线性回归模型
# 构建线性回归模型
lm_model <- lm(AQI ~ PM25 + PM10 + SO2 + CO + NO2 + O3, data = aqi_data)
# 显著性检验
summary(lm_model)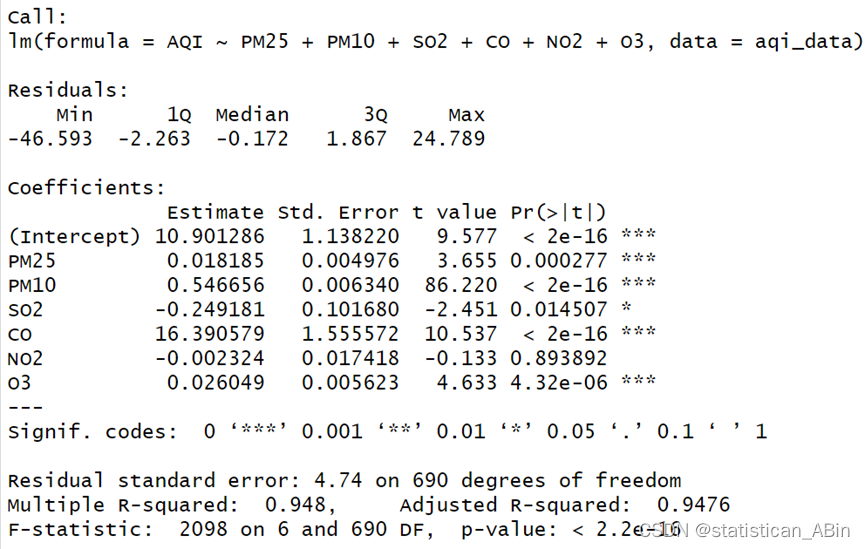 
模型公式为AQI ~ PM2.5 + PM10 + SO2 + CO + NO2 + O3。
模型的R平方值为0.948，说明该模型可以解释94.8%的AQI变化。
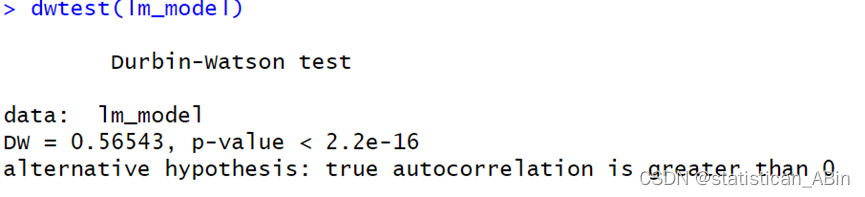
结果表明，Durbin-Watson统计量为0.56543，p值小于2.2e-16，表明残差存在显著的正自相关性
残差图
# 绘制模型诊断图
par(mfrow=c(2,2))
plot(lm_model)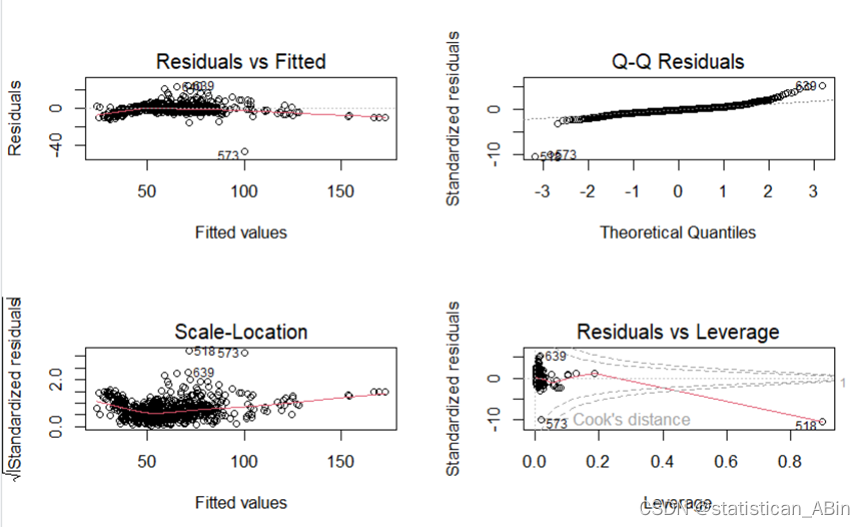
。。。总体来看，图中显示了一些异常值和高杠杆值点
# 绘制实际值与预测值对比图
ggplot(aqi_data, aes(x = datetime)) +
geom_line(aes(y = AQI, color = "实际值")) +
geom_line(aes(y = predicted_AQI, color = "预测值")) +
labs(title = "合肥四月份空气质量实际值与预测值对比", x = "时间", y = "AQI") +
scale_color_manual(values = c("实际值" = "blue", "预测值" = "red")) +
theme_minimal()+
theme(plot.title = element_text(hjust = 0.5))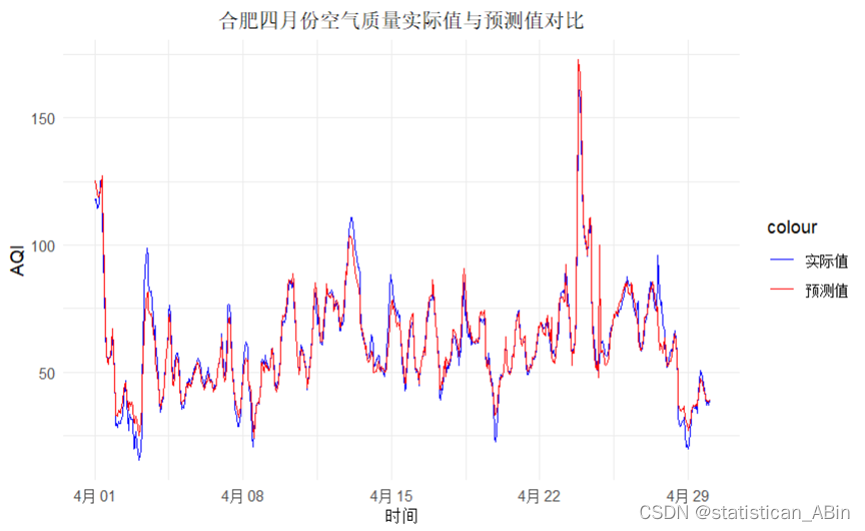
该图展示了合肥市四月份空气质量实际值与预测值的对比。图中蓝色线表示实际值，红色线表示预测值。可以看到，预测值与实际值总体趋势一致，特别是在4月1日和4月22日的高峰处。。。。
四、结论
本研究通过对2024年4月份合肥市空气质量指数（AQI）及相关污染物数据的分析，发现AQI与PM2.5和PM10之间存在显著的正相关关系，表明颗粒物是影响空气质量的主要因素。。。。本研究为合肥市空气质量的监测和治理提供了重要参考，建议进一步加强对颗粒物和其他污染物的控制，以改善空气质量。
创作不易，希望大家多点赞关注评论！！！（类似代码或报告定制可以私信）
原文地址：https://blog.csdn.net/m0_62638421/article/details/140010182
免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！