代码随想录算法训练营第十四天|递归 226.翻转二叉树 101. 对称二叉树 104.二叉树的最大深度 111.二叉树的最小深度
226.翻转二叉树
翻转一棵二叉树。
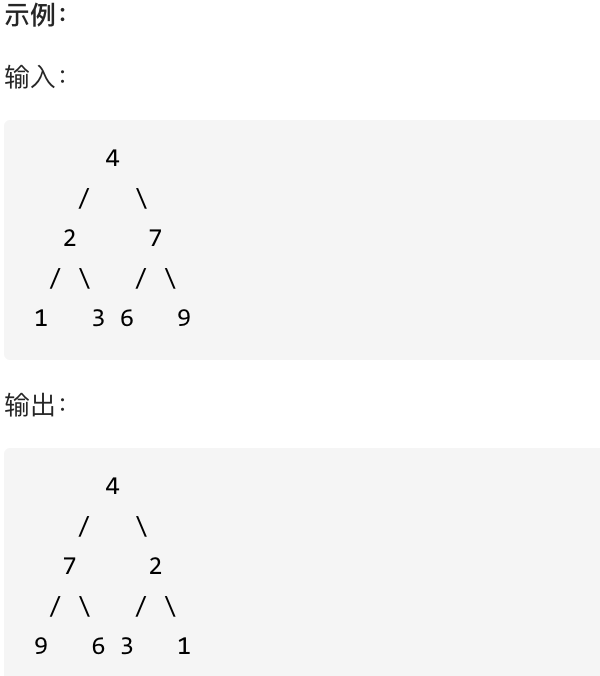
思路:
在这里需要注意的是,在递归的时候唯独中序遍历是不可用的,这是因为先对左子树进行了反转,又对自身进行了反转,对自身反转后原本的左子树变成了右子树,如果此时又轮到对右子树进行翻转,相当于原本的右子树没操作而对原来的左子树进行了两次翻转。
所以我们选择前序遍历,根据递归三部曲:
1.确定参数和返回值:参数是节点,而返回值可以是返回根节点,但我个人在一开始做的时候人为自定义了一个新的函数来专门对二叉树进行反转,是直接对二叉树进行操作的,所以认为不需要返回值,选择void或者->None
2.确定终止条件:当左孩子和右孩子都不存在的时候说明此时翻转无意义,此时return。(但规范写法的思路是当节点为空的时候return,我想这是因为如果只有一个左(右)孩子的时候依然会调用函数,这个时候有一个孩子节点是为空的,所以此时在定义递归函数的时候肯定还是需要定义一个条件:当节点为空时return,自然就不需要我一开始设置的这个条件了)
3.单层递归的逻辑:我选择最好理解的前序遍历,逻辑就是先对本节点进行操作,即对本节点的左右孩子进行互换,然后对左子树(左孩子节点)进行反转操作(调用递归),再对右子树进行反转操作。
根据以上思路,实现代码如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def reverseTree(self, node: Optional[TreeNode]) -> None:
if not node:
return
if not node.left and not node.right:
return
node.left, node.right = node.right, node.left
self.reverseTree(node.left)
self.reverseTree(node.right)
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return root
self.reverseTree(root)
return root附上规范写法,更简洁和有效,应该学习:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root以上是递归写法,自然还能用迭代的方法,个人更喜欢使用广度优先(层序遍历),非常好理解,思路就是层序遍历压入队列中,然后依次进行反转,代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return root
queue = deque([root])
while(queue):
for _ in range(len(queue)):
cur = queue.popleft()
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
cur.left, cur.right = cur.right, cur.left
return root101. 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。

思路:
第一反应还是层序遍历,只需要将包括None的每一层节点数组都压入数组中,如果将数组的每一层数组反序输出与原数组都相同,那么说明是对称的。
但还是以学习递归为主,先优先实现递归的方法,思路是在每一个递归过程中,判断【左孩子的左孩子】和【右孩子的右孩子】是否相等,以及判断【左孩子的右孩子】和【右孩子的左孩子】是否相等。代码随想录将其分别称为外侧和里侧,可能更好理解一点。除了以上还需要确保根节点的左右孩子相等才行。
递归三部曲:
- 参数和返回值:参数为两个,是左右孩子两个节点,即要进行比较的两个子树根节点。返回值应该是bool,当出现任意一个false都应该返回false。
- 终止条件:①左空右不空->false ②左不空右空->false ③左右为空->True ④左右不空但数值不等->false
- 递归逻辑:当左右不空且数值相等时(这里其实是⑤,所以上面④的时候不能用else,只能用else if或者elif),才进入递归逻辑:判断【左孩子的右孩子】和【右孩子的左孩子】是否相等,只有当两个条件都符合时返回True,否则返回false。
代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def compare(self, node1: Optional[TreeNode], node2: Optional[TreeNode]) -> bool:
if node1 and not node2:
return False
elif not node1 and node2:
return False
elif not node1 and not node2:
return True
elif node1.val != node2.val:
return False
bool1 = self.compare(node1.left, node2.right)
bool2 = self.compare(node1.right, node2.left)
return bool1 and bool2
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
if not root.left and not root.right:
return True
return self.compare(root.left, root.right)规范代码:
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
return self.compare(root.left, root.right)
def compare(self, left, right):
#首先排除空节点的情况
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
#排除了空节点,再排除数值不相同的情况
elif left.val != right.val: return False
#此时就是:左右节点都不为空,且数值相同的情况
#此时才做递归,做下一层的判断
outside = self.compare(left.left, right.right) #左子树:左、 右子树:右
inside = self.compare(left.right, right.left) #左子树:右、 右子树:左
isSame = outside and inside #左子树:中、 右子树:中 (逻辑处理)
return isSame层序遍历:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
res = []
queue = deque([root])
while queue:
arr = []
for _ in range(len(queue)):
cur = queue.popleft()
if not cur:
arr.append(None)
continue
arr.append(cur.val)
queue.append(cur.left)
queue.append(cur.right)
res.append(arr)
for arr in res:
if arr != arr[::-1]:
return False
return True规范代码(层序遍历):
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque([root.left, root.right])
while queue:
level_size = len(queue)
if level_size % 2 != 0:
return False
level_vals = []
for i in range(level_size):
node = queue.popleft()
if node:
level_vals.append(node.val)
queue.append(node.left)
queue.append(node.right)
else:
level_vals.append(None)
if level_vals != level_vals[::-1]:
return False
return True104.二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
思路:
依然第一反应是层序遍历:每到新一层就更新最大值,最后返回最大值即可。
还是以学习递归为主,递归思路:
节点的深度是孩子节点的深度+1,那么只需要递归计算孩子节点的深度然后+1即可。
递归三部曲:
- 参数和返回值:参数应该是传入一个节点。返回值是传入节点的两个孩子节点的深度的最大值,应该是int类型。
- 终止条件:当左右孩子都不存在的时候,说明是叶子节点,此时返回深度1。当本节点不存在的时候,这时候为了区别于叶子节点,返回深度0
- 递归逻辑:对两个左右孩子进行递归调用,得到两个数值中的最大值然后再+1就可以得到当前节点的深度。
代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getdepth(self, node: Optional[TreeNode]) -> int:
if not node:
return 0
if not node.left and not node.right:
return 1
return max(self.getdepth(node.left), self.getdepth(node.right)) + 1
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return self.getdepth(root)层序遍历:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
queue = deque([root])
res = 0
while queue:
for _ in range(len(queue)):
cur = queue.popleft()
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
res += 1
return res
111.二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最小深度 2.
思路:
层序遍历思路:每层遍历记录层数,当第一次遍历到叶子节点的时候直接返回深度即可。
递归思路:与前面计算最大深度相似,但是需要注意的是,有一种情况不一样,也就是只有一个孩子的情况,因为没有孩子的情况有可能会返回0,但此时本节点并非叶子节点,此时如果空节点返回了深度0,那么此时计算到的最小深度是错误的。所以该题应该在遇到空孩子的时候直接跳过。
递归三部曲:
- 参数和返回值:参数是进入递归调用的节点。返回值应该是int类型的深度值。
- 终止条件:当左右孩子都不存在时(为叶子节点),返回深度1
- 递归逻辑:当左右孩子均存在时,计算两个孩子节点的深度的最小值,得到后+1作为返回值。如果只存在一个孩子,则计算存在的孩子节点的深度,然后+1作为返回值。、
代码实现如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
return self.getdepth(root)
def getdepth(self, node: Optional[TreeNode]) -> int:
if not node:
return 0
if not node.left and not node.right:
return 1
if node.left and node.right:
return min(self.getdepth(node.left), self.getdepth(node.right)) + 1
elif not node.left and node.right:
return self.getdepth(node.right) + 1
elif node.left and not node.right:
return self.getdepth(node.left) + 1规范代码:
class Solution:
def getDepth(self, node):
if node is None:
return 0
leftDepth = self.getDepth(node.left) # 左
rightDepth = self.getDepth(node.right) # 右
# 当一个左子树为空,右不为空,这时并不是最低点
if node.left is None and node.right is not None:
return 1 + rightDepth
# 当一个右子树为空,左不为空,这时并不是最低点
if node.left is not None and node.right is None:
return 1 + leftDepth
result = 1 + min(leftDepth, rightDepth)
return result
def minDepth(self, root):
return self.getDepth(root)层序遍历:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
queue = deque([root])
res = 0
while queue:
for _ in range(len(queue)):
cur = queue.popleft()
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
if not cur.left and not cur.right:
return res+1
res += 1
return res原文地址:https://blog.csdn.net/weixin_47681529/article/details/142501112
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
