3月14日分割回文串（双指针/记忆化搜索/动态规划+回溯）

131.分割回文串

131. 分割回文串 - 力扣（LeetCode）

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 

回文串

 。返回 s 所有可能的分割方案。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

提示：

• 1 <= s.length <= 16
• s 仅由小写英文字母组成

思路

这道题目回溯的思想主要体现在截取子串的过程中，以abaa为例画出树形图，从第一位截到最后一位，一开始截取a，然后对a进行判断是不是回文串，发现是之后继续对剩下的baa进行分割操作，首先对baa截取b，再截取ba，此时发现ba不是回文串，所以直接剪枝。整个递归的流程是建立在当前截取的子串是回文子串之后才会继续进行下去。

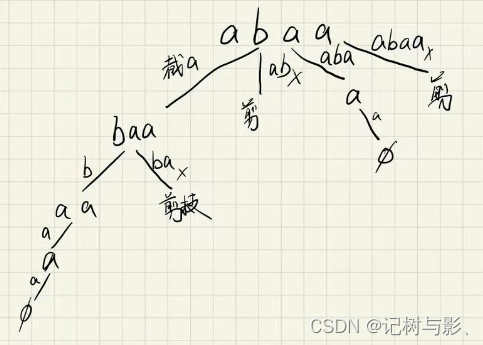
判断字符串是否为回文串的方法常见的就是双指针法

    class Solution {
        public List<List<String>> partition(String s) {
            int len=s.length();
            List<List<String>> res=new ArrayList<>();
            if(len==0){
                return res;
            }
            Deque<String> stack=new ArrayDeque<>();
            char[] charArray=s.toCharArray();
            dfs(charArray,0,len,stack,res);
            return res;
        }
        public void dfs(char[] charArray,int index,int len,Deque<String> path,List<List<String>> res){
            if(index==len){
                res.add(new ArrayList<>(path));
                return;
            }
            for(int i=index;i<len;i++){
                if(!checkPalindrome(charArray,index,i)){
                    continue;
                }
                path.addLast(new String(charArray,index,i+1-index));
                dfs(charArray,i+1,len,path,res);
                path.removeLast();
            }

        }
        public boolean checkPalindrome(char[] charArray,int left,int right){
            while(left<right){
                if(charArray[left]!=charArray[right]){
                    return false;
                }
                left++;
                right--;
            }
            return true;
        }
    }

动态规划法

回文子串的性质：如果子串s[i]...s[j]是回文子串，那么s[i+1]...s[j-1]一定也是回文子串。

初始条件

满足如下条件的子串都是回文子串：

• 空字符串是回文子串；
• 所有长度为1的子串也是回文子串

状态转移

依次枚举所有子串的长度，并枚举子串的左侧边界：

• 如果便且两侧的字符不相等，那么该子串一定不是回文子串；
• 如果边界两侧的字符相等，则当前子串的状态，与去掉首尾字符后的子串的状态相同。

因此状态转移方程为

 通过dp[i][j]就可以在O(1)的时间复杂度内，判断子串是否为回文子串。

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

public class Solution {

    public List<List<String>> partition(String s) {
        int len = s.length();
        List<List<String>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        char[] charArray = s.toCharArray();
        // 预处理
        // 状态：dp[i][j] 表示 s[i][j] 是否是回文
        boolean[][] dp = new boolean[len][len];
        // 状态转移方程：在 s[i] == s[j] 的时候，dp[i][j] 参考 dp[i + 1][j - 1]
        for (int right = 0; right < len; right++) {
            // 注意：left <= right 取等号表示 1 个字符的时候也需要判断
            for (int left = 0; left <= right; left++) {
                if (charArray[left] == charArray[right] && (right - left <= 2 || dp[left + 1][right - 1])) {
                    dp[left][right] = true;
                }
            }
        }

        Deque<String> stack = new ArrayDeque<>();
        dfs(s, 0, len, dp, stack, res);
        return res;
    }

    private void dfs(String s, int index, int len, boolean[][] dp, Deque<String> path, List<List<String>> res) {
        if (index == len) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = index; i < len; i++) {
            if (dp[index][i]) {
                path.addLast(s.substring(index, i + 1));
                dfs(s, i + 1, len, dp, path, res);
                path.removeLast();
            }
        }
    }
}

总结

动态规划完全没懂，这里先开个头，之后再详细展开。

原文地址：https://blog.csdn.net/qq_39911747/article/details/136698903

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！