C++ 数论相关题目：卡特兰数应用、快速幂求组合数。满足条件的01序列

给定 n
个 0
和 n
个 1
，它们将按照某种顺序排成长度为 2n
的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0
的个数都不少于 1
的个数的序列有多少个。

输出的答案对 109+7
取模。

输入格式
共一行，包含整数 n
。

输出格式
共一行，包含一个整数，表示答案。

数据范围
1≤n≤105
输入样例：
3
输出样例：
5

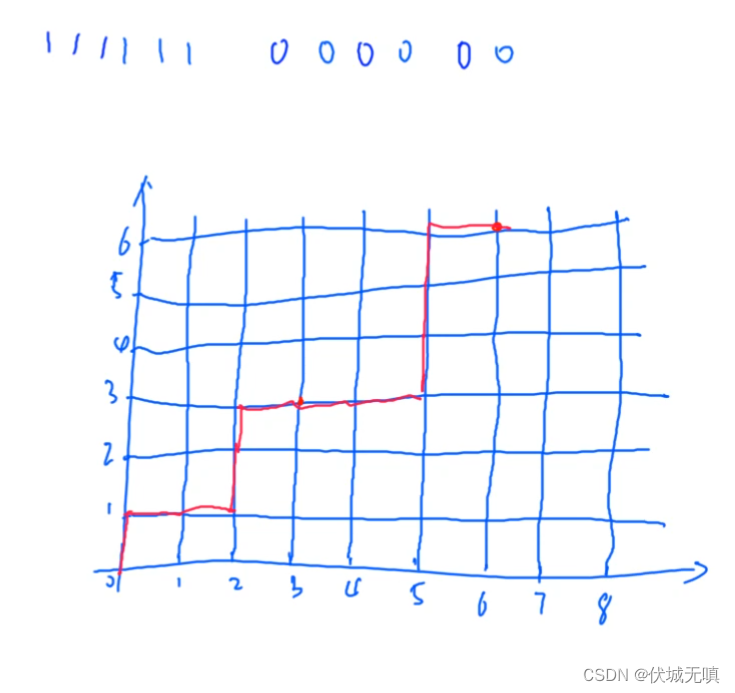
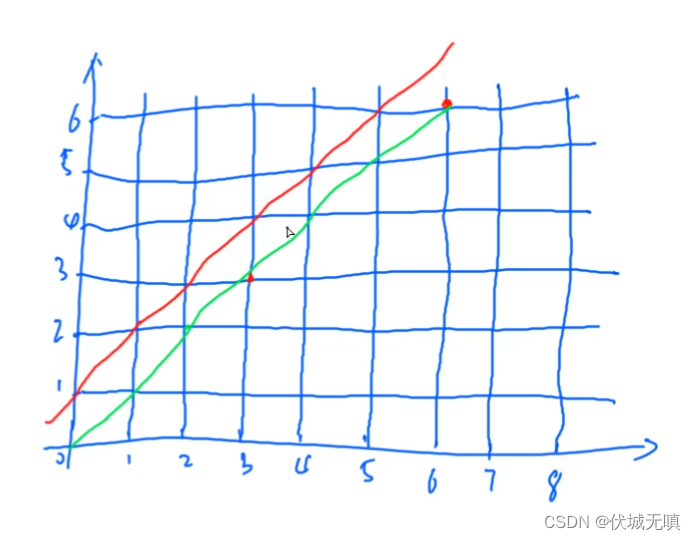
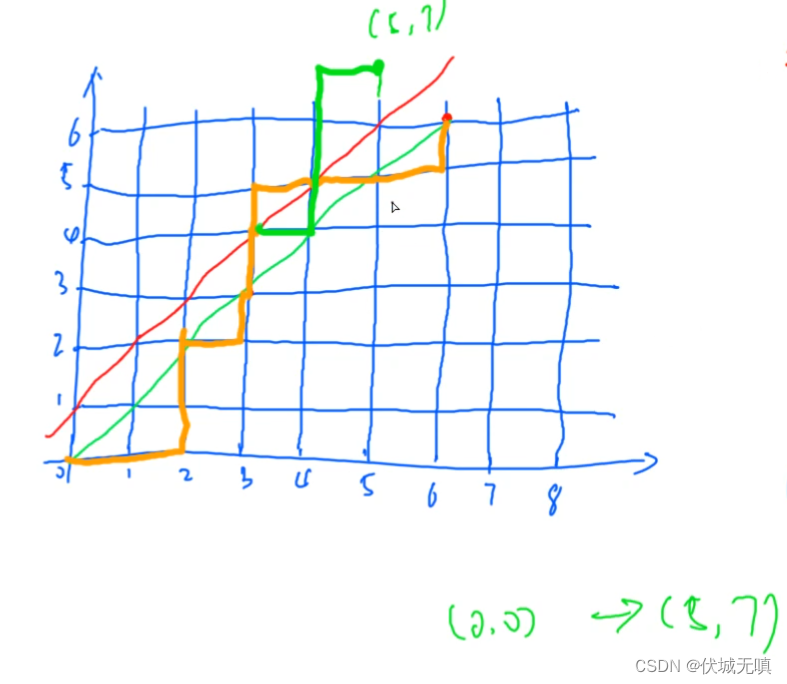
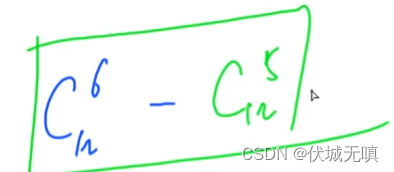
上述描述了本题的公式推导，最终也就是求一个卡特兰数。
本题中，求逆元取模的是一个质数，可以用快速幂来求，如果不是质数的话，只能用扩展欧几里得算法来求。

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;
int n;

int qmi(int a, int k, int p)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int main ()
{
    cin>>n;
    int a = 2 * n, b = n;
    int res = 1;
    
    for(int i = a; i > a - b; i -- ) res = (LL)res * i % mod;
    for(int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;
    
    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
    cout<<res<<endl;
    return 0;
}

原文地址：https://blog.csdn.net/qq_45281807/article/details/135921712

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！