力扣958：判断二叉树是否为完全二叉树

给你一棵二叉树的根节点 root ，请你判断这棵树是否是一棵 完全二叉树 。

在一棵 完全二叉树 中，除了最后一层外，所有层都被完全填满，并且最后一层中的所有节点都尽可能靠左。最后一层（第 h 层）中可以包含 1 到 2h 个节点。

示例 1：

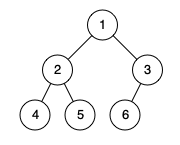
输入：root = [1,2,3,4,5,6]
输出：true
解释：最后一层前的每一层都是满的（即，节点值为 {1} 和 {2,3} 的两层），且最后一层中的所有节点（{4,5,6}）尽可能靠左。

示例 2：

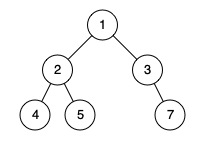
输入：root = [1,2,3,4,5,null,7]
输出：false
解释：值为 7 的节点不满足条件「节点尽可能靠左」。

提示：

• 树中节点数目在范围 [1, 100] 内
• 1 <= Node.val <= 1000

思想：将二叉树全部入队，然后扫描队中的元素，如果出现为空，则判断后续是否还有元素，如果有，则不是完全二叉树，如果没有，则是完全二叉树。

代码：

bool isCompleteTree(struct TreeNode* root){
    /*if(root==NULL)//完全二叉树可以为空
    {
        return true;
    }*/
    struct TreeNode *queue[20000];
    int rear=0,front=1;
    queue[rear]=root;//根节点入队
    while(rear<front)
    {
        if(queue[rear]==NULL)//这里包含了空二叉树
        {
            rear++;
        }
        else
        {
            //左右子树入队
            queue[front++]=queue[rear]->left;
            queue[front++]=queue[rear]->right;
            rear++;//左右子树分别向下遍历
        }
    }
    for(int i=0;i<front;i++)//遍历队列
    {
        if(queue[i]==NULL)
        {
            for(int j=i+1;j<front;j++)//当出现为空时，如果后面还有元素，则不是完全二叉树
            {
                if(queue[j]!=NULL)
                {
                    return false;
                }
            }
        }
    }
    return true;
}

时间复杂度O（n）；空间复杂度O（n）

原文地址：https://blog.csdn.net/m0_56332819/article/details/142501752

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！