python-数据分析与可视化基础
1、data1.csv中的B、C、D和E列数据分别是日期、权重、A企业的销售额、B企业的销售额。读取C、D、E列数据,并统计E列数据的算术平均数、加权平均值(权值为C列数据)、方差、中位数、最小值、最大值。并绘制E列数据的直方图。
(1)源代码:
import numpy as np
import matplotlib.pyplot as plt
C, D, E = np.loadtxt("data1.csv", delimiter=',', usecols=(2, 3, 4), unpack=True, skiprows=1)
sum1 = np.sum(E)
print("E企业的销售额总和:", sum1)
mean1 = np.mean(E)
print("E企业的销售额的算术平均数:", mean1)
wavg1 = np.average(E, weights=C)
print("E企业的销售额的加权平均值为:", wavg1)
var1 = np.var(E)
print("E企业的销售额的方差为:", var1)
media1 = np.median(E)
print("E企业的销售额的中位数为:", media1)
min1 = np.min(E)
print("E企业的销售额的最小值:", min1)
max1 = np.max(E)
print("E企业的销售额的最大值:", min1)
plt.hist(E, bins=10, rwidth=0.8)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlabel('E企业的销售额', fontsize=15)
plt.ylabel('出现次数', fontsize=15)
plt.title('E企业的销售额分布直方图', fontsize=18)
plt.show()(2)运行结果截图 :
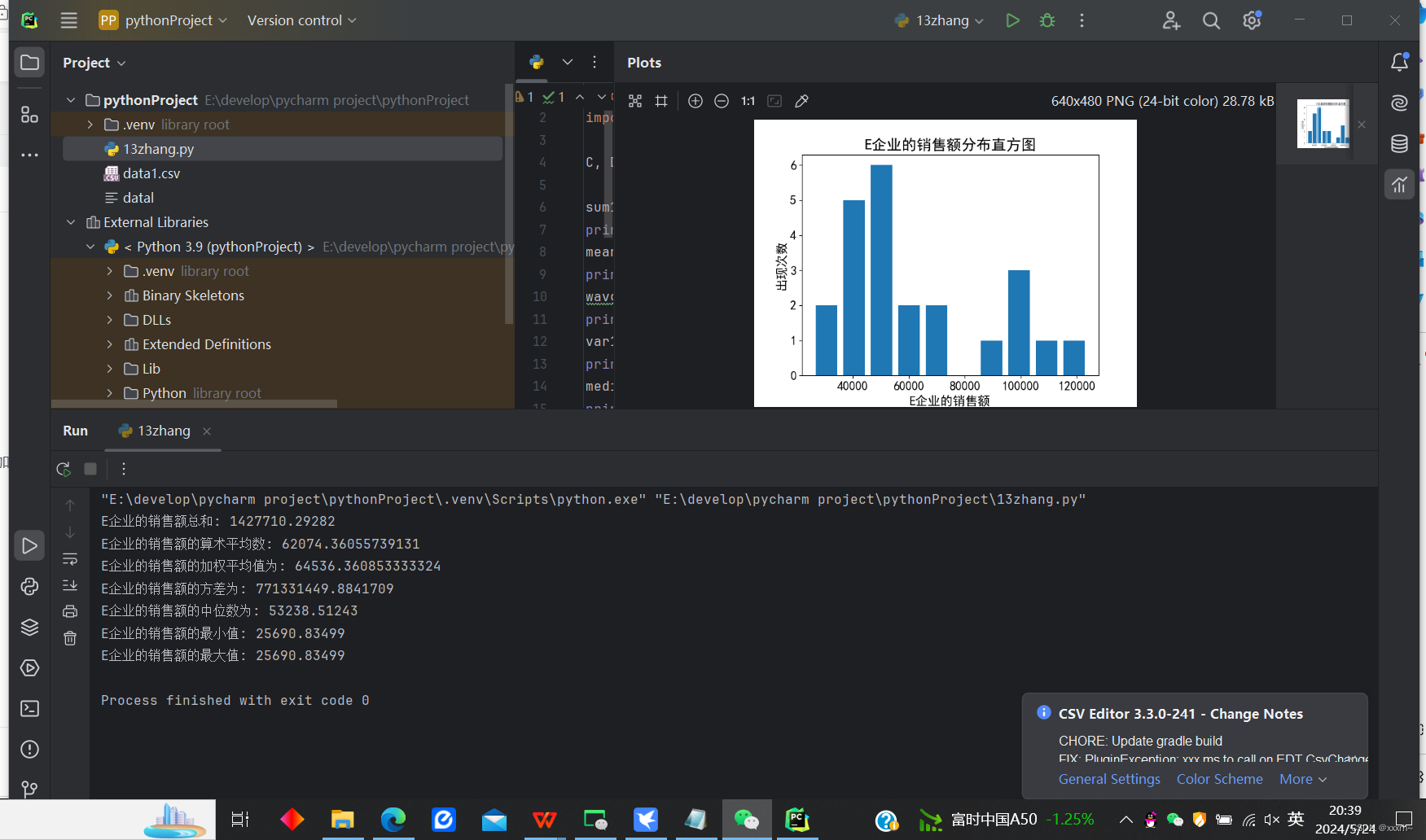
2、读取data1.csv文件中的A企业销售额与B企业销售额数据,并计算这些企业数据的协方差矩阵和相关系数矩阵。
(1)源代码:
import numpy as np
A, B = np.loadtxt('data1.csv', delimiter=',', usecols=(3, 4), unpack=True, skiprows=1)
covAB = np.cov([A, B])
relAB = np.corrcoef([A, B])
print('A,B企业数据的协方差矩阵为:')
print(covAB)
print('A,B企业数据的相关系数矩阵为:')
print(relAB)(2) 运行结果截图 :

3、读取 datal.csv文件中A、B、C、D、E,绘制由A列和D列数据关联,以及由A列和E列数据(请将该列值除以120后绘图)关联的两条折线图,并分别赋以不同的颜色和线型,添加图例。
(1)源代码
import numpy as np
import matplotlib.pyplot as plt
s, a, b = np.loadtxt('data1.csv' , delimiter=',' ,
usecols=(0 , 3 , 4), unpack=True , skiprows=1)
plt.plot(s, a,'r*--',alpha=0.5,linewidth=1,label='A企业')
plt.plot(s,b/120,'go--',alpha=0.5,linewidth=1, label='B企业')
plt.rcParams['font.sans-serif']=['SimHei']
plt.legend()
plt.xlabel('时间')
plt.ylabel('销售额')
plt.title('A企业与B企业销售额走势图')
plt.show()(2)运行结果截图

4、针对data1.csv中A企业的销售额,使用简单移动平均方法估计各月的销售额。移动平均间隔为3,即用1、2、3三周的数据预测第4周的数据。
(1)源代码
import numpy as np
import matplotlib.pyplot as plt
a= np.loadtxt('data1.csv',delimiter=',',usecols=3, unpack=True , skiprows=1)
winwide =3
weight = np.ones(winwide)/winwide
plt.rcParams['font.sans-serif']=['simHei']
aM = np.convolve(weight,a)
t = np.arange(winwide-1,len(a))
plt.figure(figsize=(15,10))
plt.subplot(1,2,1)
plt.plot(t,a[winwide-1:],lw=1.0,label='实际A企业的销售额')
plt.plot(t, aM[winwide-1:1-winwide],lw=3.0, label='A企业销售额的移动平均值')
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.grid()
plt.title('A企业销售额',fontsize=18)
plt.legend(fontsize=10)
plt.subplots_adjust(wspace=0.2)
plt.show()(2)运行结果截图

5.使用指数移动平均方法估计上题的A企业的销售额。移动平均间隔为3。并请添加图、坐标轴标题和图例。
(1)源代码
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
volume = np.loadtxt('data1.csv',delimiter=','
,usecols=3, unpack=True, skiprows=1)
winwide = 3
print('0bservation:\n',volume)
t= np.arange(winwide-1,len(volume))
print('time:\n',t)
weights = np.exp(np.linspace(-1,0,winwide))
weights /= weights.sum()
print('weights:\n',weights)
weightMovingAVG =np.convolve(weights,volume)
print('Prediction:\n',weightMovingAVG)
plot1 = plt.plot(t,volume[winwide-1:],lw=1.0)
plot2 = plt.plot(t, weightMovingAVG[winwide-1:1-winwide], lw=2.0)
plt.title('A销售额指数移动平均',fontsize=18)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlabel('时间顺序',fontsize=15)
plt.ylabel('A企业销售额',fontsize=15)
plt.legend((plot1[0],plot2[0]),('真实值','指数移动平均值'),
loc='upper right',fontsize=13,numpoints=1)
plt.show()(2)运行结果截图
原文地址:https://blog.csdn.net/m0_64809275/article/details/139183996
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
