二维费用背包问题
1. 一和零

题目中是在一个字符串数组中找出一个最大子集,满足 0 和 1 的个数不超过给定的值,这和之前的背包问题不一样的是,这里有两个限制条件,也就是二维费用背包问题,同时,这道题也是一道 01 背包的模型
状态表示:
dp[i][j][k] 表示,在前 i 个物品中挑选,字符 0 的个数不超过 j ,字符 1 的个数不超过 k ,所有选法中最大的子集长度
状态转移方程:
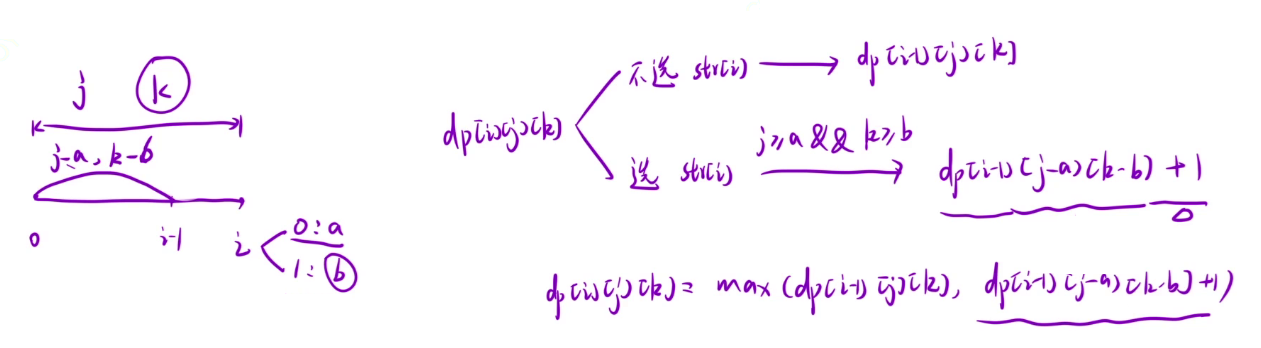
还是可以分为选和不选第 i 个元素,如果不选的话,那么 dp[i][j][k] 的状态就还是上一个状态,也就是 dp[i - 1][j][k] ,如果选的话,是需要保证 j >= a 并且 k >= b,然后才能更新为 dp[i - 1][j - a][k - b] + 1,由于题目中是求最大的子集,所以这两种情况还需要求出最大值(第二种情况存在时)
初始化:使用 j 和 k 时,是需要判断的,所以这两列就不用初始化了,当 i = 0 时,也就是字符串数组为空,找出子集,所以 i = 0 时,这一面就都是0 了
填表顺序:由于需要用到 i - 1 的状态,所以需要保证 i 从小到大遍历,然后再从小到大遍历 j 和 k
返回值:dp[len][m][n]
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int len = strs.length;
int[][][] dp = new int[len + 1][m + 1][n + 1];
for (int i = 1; i <= len; i++) {
int a = 0, b = 0;
for (int x = 0; x < strs[i - 1].length(); x++) {
if (strs[i - 1].charAt(x) == '0')
a++;
else
b++;
}
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
dp[i][j][k] = dp[i - 1][j][k];
if (j >= a && k >= b) {
dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1);
}
}
}
}
return dp[len][m][n];
}
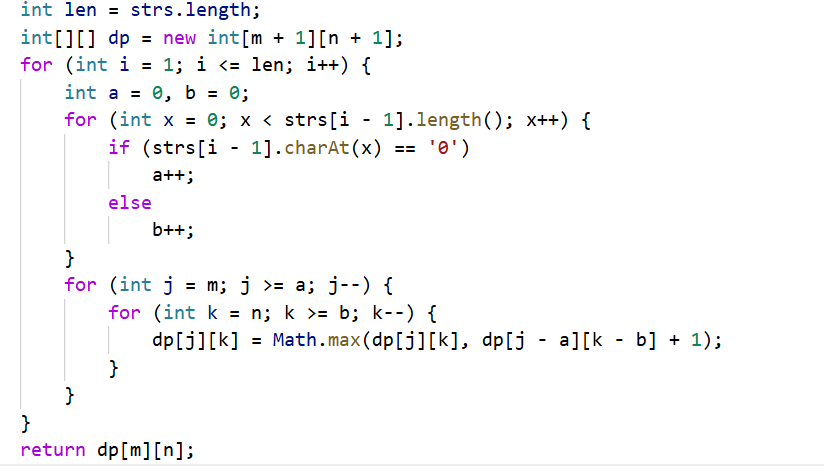
}空间优化:
二维费用的背包问题的优化和一维的是一个道理,把第一列的删掉就可以了
2. 盈利计划

状态表示:
还是参考二维费用背包问题的状态表示方法
dp[i][j][k] 表示从前 i 个计划中选,总人数不超过 j ,总利润至少为 k ,有多少种选法
状态转移方程:

还是分为选和不选第 i 个元素,如果不选就是继承上一个状态 dp[i - 1][j][k],如果选,由于总人数不能超过 j ,是需要 j >= g[i] 的,也就是 j - g[i] 不能小于 0,而总利润至少为 k ,所以 k - p[i] 是可以小于 0 的,但是数组的下标也不能是负的,所以可以把总利润至少为(之前的负数)改为总利润至少为 0,题中求的是总的方案数,所以最终结果是这两种情况的和
初始化:由于填表是从下标为 1 开始的,所以把下标为 0 初始化一下即可,当 i = 0 时,也就是没有任务,此时的利润也是 0 ,所以不管用多少人数限制是多少,总利润都是 0,需要初始化的也就是人数 j 这一列,方案数都是 1(什么都不选),dp[0][j][0] 都是 1
填表顺序:和上一题一样,只需要保证 i 是从小到大即可
class Solution {
public int profitableSchemes(int n, int m, int[] g, int[] p) {
int len = g.length;
int[][][] dp = new int[len + 1][n + 1][m + 1];
//初始化
for (int j = 0; j <= n; j++)
dp[0][j][0] = 1;
for (int i = 1; i <= len; i++) {
for (int j = 0; j <= n; j++) {
for (int k = 0; k <= m; k++) {
dp[i][j][k] = dp[i - 1][j][k];
if (j >= g[i - 1]) {
dp[i][j][k] += dp[i - 1][j - g[i - 1]][Math.max(0, k - p[i - 1])];
}
dp[i][j][k] %= (int) (1e9 + 7);
}
}
}
return dp[len][n][m];
}
}空间优化:
空间优化还是去掉第一列,由于是 01 背包模型,所以之后的循环都是降序

原文地址:https://blog.csdn.net/2202_76097976/article/details/143770737
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
