【Pytorch: Deepwave】GPU引领的正演与数值全波形反演 (FWI)

0. Deepwave的基本介绍

Deepwave是一个强大的使用有限差分法实现波动方程的正演和数值迭代反演的Python库.
相比于一般的基于Matlab或者常规代码实现的正演或者数值迭代反演, Deepwave利用了Pytorch可调用GPU进行反向传递和求导的特点, 具备更强大的运算性能.
实际上的话, Deepwave封装了大量的面向地球科学领域的可运用的算法, 它包括标量波动方程的2D正则和Born建模、弹性波动方程的正演、RTM、LSRTM、联合偏移反演等等.
本博客主要侧重于如何使用一些简单的内容, 侧重给偏计算机的研究人员调用.
如果想了解完整的代码和使用例子可通过其作者 (Alan Richardson) 的Github主页和文档说明来了解. 本文也将基于文档说明中的例子来延伸.

本篇的实验是基于Deepwave最新版本 (2024.5.14) v0.0.20
要获得这个版本你可以采用以下两种途径:

1. cmd 的 pip install deepwave 然后用pip list检查一下版本是否对应, 如果版本不对应, 可能你需要使用途径2
2. (针对windows) 到这里下载v0.0.20的zip版本, 然后解压到随便一个路径. 然后使用cmd的命令cd /d X:\XXX\XXX\deepwave-0.0.20 移动到这个路径, 执行pip install .来离线安装

1. Pytorch的自动求导机制

我们往往关注Pytorch在神经网络搭建上的便利而往往忽略了其最基本两项优秀的特性:

1. 调用GPU (借助Tensor)
2. 自动求导

为了搭建在GPU上, Pytorch创建一种不同于Numpy中的ndarray的全新数据结构: Tensor.
创建一个Tensor并将其搭建在GPU可以通过如下代码实现:

a = torch.arange(3)  # [0, 1, 2] (搭载于CPU)
b = torch.ones(3, device=torch.device('cuda'))  # [1, 1, 1] (搭载于GPU)
c = a.cuda()**2 + 2 * b  # [2, 3, 6] (搭载于GPU)
d = c.cpu()  # d = [2, 3, 6] (搭载于CPU), c仍然在GPU上

这种相互换载的手段需要注意的地方在于: 不同平台的变量之间是不能相互干涉计算的.

自动求导的关键是变量之间构成的关于梯度的链式关系.
例如下面这样的例子:

a = torch.arange(3.0, requires_grad=True)
b = (2 * a).sum()
print(b)# tensor(6., grad_fn=<SumBackward0>)
b.backward()
print(a.grad_fn)# None
print(b.grad)# None
print(a.grad)# tensor([2., 2., 2.])

在这里, 我们创建了一个Tensor变量a, 包含[0, 1, 2]并表明我们需要记录这个变量的梯度.
requires_grad=True是一个关键的声明, 声明之后对于这个变量的所有操作都将被追踪.
此外对于任意变量使用.requires_grad_()方法也可以手动开启追踪.
如果希望当前代码中如此标记的变量不被追踪, 可以用with torch.no_grad()包裹住目标代码来临时取消追踪.
如果想完全清除一个变量的所有"追踪"记录, 也可以直接使用.detach()

b是a通过求和操作得到的变量.
输出b的时候可以看见其grad_fn属性为<SumBackward0>.
这告知了两个信息: 首先, 因为a是被"追踪"的变量, 且b的运算包括了这个变量, 于是其也被"追踪";
其次, 因为b是对a求和得到的, 因此b包含对它的操作的伴随项a的引用"grad_fn=<SumBackward0>".
而a作为这个运算链的末尾叶子结点, 其grad_fn值为None. 这个运算链如下图

因为b触发了backward运算后, 以b为起点, 向它下方的所有节点传递, 计算所有requires_grad为True的变量的梯度grad.
但是b本身是没有梯度的, 因为这个节点并不是直接设置requires_grad为True的节点.
然后我们试图建立一个稍微复杂一点的求导链:

a = torch.arange(3.0, requires_grad=True)
b = (2 * a).sum()
c = torch.ones(3, requires_grad=True)
d = (a * c).sum() + b

print(d.grad_fn)# <AddBackward0 object at 0x000001700D36AA20>
print(c.grad_fn)# None
print(b.grad_fn)# <SumBackward0 object at 0x000001DB1E6DAA58>
print(a.grad_fn)# None

d.backward()

print(d.grad)# None
print(c.grad)# tensor([0., 1., 2.])
print(b.grad)# None
print(a.grad)# tensor([3., 3., 3.])

从grad_fn可以发现, c与b作为叶子, 不是任何操作的结果, 因此没有对应的grad_fn值. 下图所示

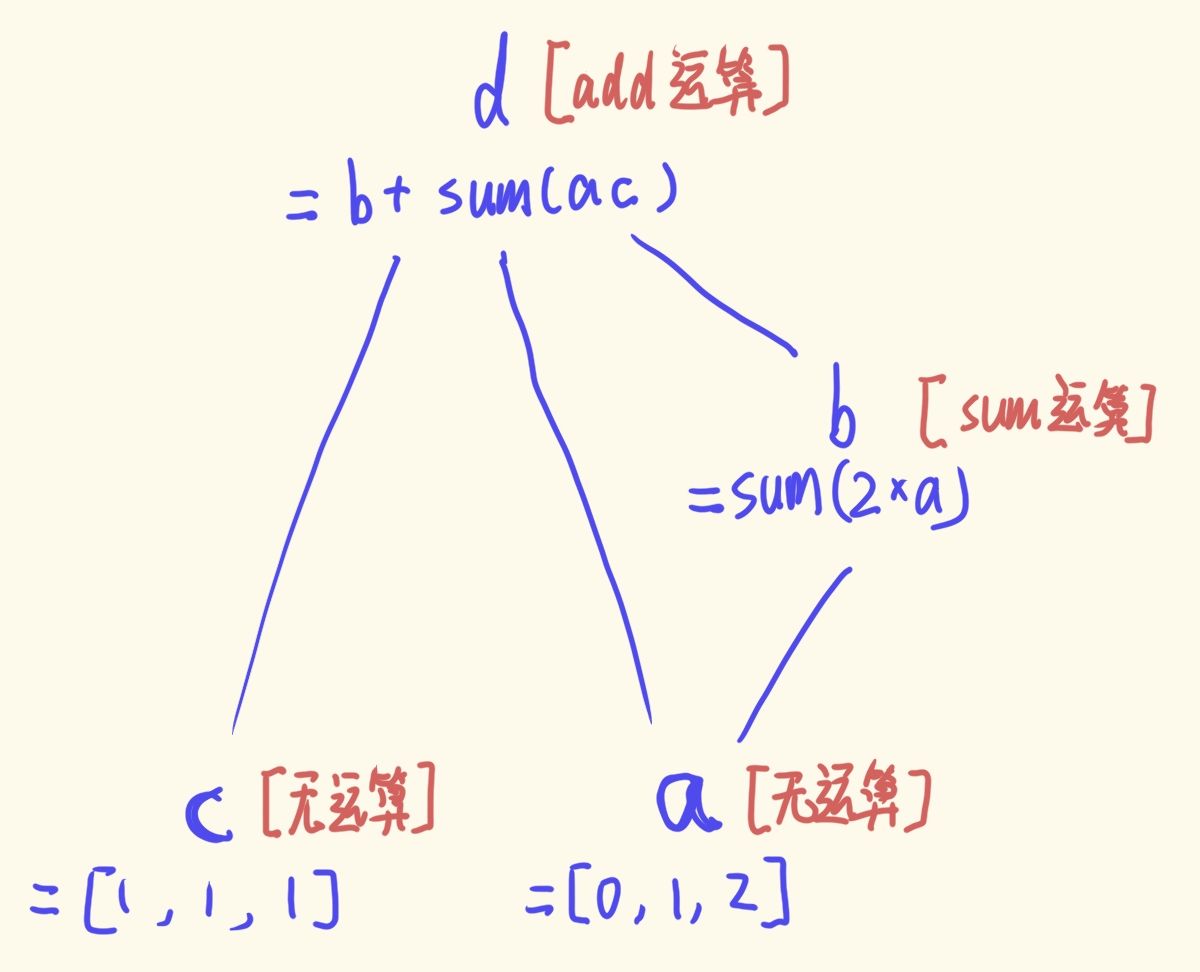
而在d触发.backward()操作后, 这个链状结构将向下传递, 更新所有设置requires_grad为True的节点的grad值 (在不求导之前, 这些梯度值是None).
需要注意, 这里a变量的梯度是两条链路共同影响的结果.
如果我们不是对d使用.backward()而是对b使用, 那么最终c的grad就是None, 而a的梯度只有[2,2,2]

同时, 要注意一个问题, 假如我们在上个例子的基础上再重新声明d和b式子并对d使用.backward(), 那么我们会得到下面的结果:

...

b = (2 * a).sum()
d = (a * c).sum() + b
d.backward()

print(c.grad)# tensor([0., 2., 4.])
print(a.grad)# tensor([6., 6., 6.])

这个结果并不是出错了, 而是新的求导得到的梯度将叠加在旧梯度之上.
当你想计算许多数据样本的梯度, 但又没有足够的内存同时处理所有样本时, 这就很有用了, 因为这样可以分批处理并累积梯度.

Deepwave作者认为: 当要计算许多镜头的梯度时, 就会出现这种情况

如果要清空之前的梯度, 一种较为快捷的方式就是重新声明. 或者在使用了优化器的基础上, 对优化器使用zero_grad()
这个对于网络的batch计算是必要的, 因为当前batch计算得到的梯度并不会沿用到下次计算.

2. Pytorch实现最小化的机制

既然提到了优化器, 我们可以看下Pytorch的优化器可以做到什么程度.
PyTorch 提供了多种优化器, 你也可以使用梯度创建自己的优化器. 作为一个例子, 这里我们将介绍一个随机梯度下降法 (Stochastic Gradient Descent) 的最小化例子.

import torch

def f(x):
    return 3 * (torch.sin(5 * x) + 2 * torch.exp(x))

x_true = torch.tensor([0.123, 0.321])
y_true = f(x_true)

x = torch.zeros(2, requires_grad=True)
opt = torch.optim.SGD([x], lr=1e-4)
loss_fn = torch.nn.MSELoss()

for i in range(2000):
    opt.zero_grad()
    y = f(x)
    loss = loss_fn(y, y_true)
    print(y.grad_fn)# <MulBackward0 object at 0x000001EE93DE2F28>
    print(loss.grad_fn)# <MseLossBackward0 object at 0x000001EE93DE2F28>
    loss.backward()
    opt.step()

print(x)# tensor([0.1230, 0.3210], requires_grad=True)

这里构建了一个曲线, 两个目标点和两个重叠于 $(2,f(2))$ 的初始解.
根本目标为: 从初始解出发来拟合目标点.

首先, 我们设置了一个"SGD优化器" (Pytorch的优化器中封装各种梯度下降的算法).
SGD具备两个参数, 一个是自变量参数$x$, 一个是下降的步长.

其次, 实现一轮梯度下降须知道一个函数关于这个自变量$x$的梯度. 因为

1. 理论上, 关于$x$的函数是得知$x$的下一步挪动方向/大小的基础.
2. 代码逻辑上, 计算梯度至少需要一个对$x$的运算链的结构, 仅有一个$x$肯定没法算梯度.

对于最小化问题, 这个函数往往用包含$f(x)$与目标$y_{\text{true}}$的MSE来表示.
其运算链如下:

只要我们在loss执行.backward()操作就可以顺着这条链路更新到唯一设置requires_grad为True的变量, 即$x$.

最后, 得到梯度后, 通过对优化器opt使用.step()方法来更新$x$.
因为优化器在声明时就与$x$相互关联, 因此调用$x$的梯度与更新$x$都是自然而然的.

每次迭代开始时, 我们都会将存储在 x.grad 中的梯度清零, 因为累积梯度是没有意义的.
通过迭代2000次, $x$的位置与目标位置重叠, 距离最小化成功.

如上所述, Pytorch 可以在整个计算链中进行端到端的反向传播, 计算损失函数相对于潜向量的梯度, 以及计算中涉及的任何其他变量 (required_grad=True). 这个简单例子其实就包含了数值反演的思想, 希望诸位现在能明白 Deepwave 的用处, 它不过是将这里以$f(\cdot )$为代表的乘法和正弦等运算用GPU的正演运算来实现.

3. Deepwave的正演

Deepwave调用scalar方法实现了基于声波的正演.
下面通过一个例子来了解scalar的使用:

3.1 正演的观测系统准备

首先我们先确定scalar需要的参数以及它的构造形式:

v = v.T# v是numpy的速度模型 (转置前如下图)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

ny = 140
nx = 140
dx = 5

n_shots = 7

# 震源位置参数
n_sources_per_shot = 1                  # 一个地震记录有几个源
d_source = 20                           # 20 * 5m = 100m
first_source = 10                       # 10 * 5m = 50m
source_depth = 0                        # 0 * 5m = 0m

# 接收器位置参数
n_receivers_per_shot = 140              # 一个地震记录有几个接收器
d_receiver = 1                          # 1 * 5 = 5m
first_receiver = 0                      # 0 * 5 = 0m
receiver_depth = 0                      # 0 * 5 = 0m

# 其余参数
freq = 25
nt = 1000
dt = 0.001
peak_time = np.min(v) / 1000 / freq# 震源持续波长

v = torch.tensor(v).to(device)# 正演全程需要使用GPU, 因此全程使用Tensor数据

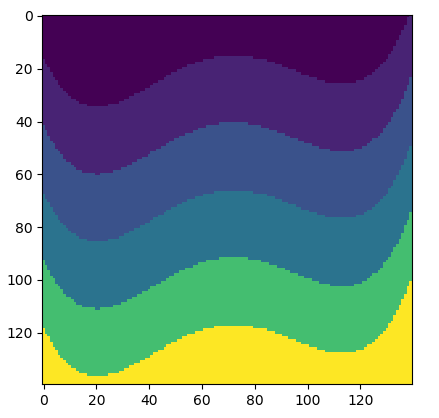
代码描述了我们的观测系统.
基本的, 速度模型的大小是一个$700m\times 700m$的地下区域, 交错网络采样大小为$5m\times 5m$, 因此速度模型的采样大小为$140\times 140$ (如上图), 速度分为六层, 自上到下依次是$1836$, $2077$, $2449$, $2770$, $3547$, $4280$ (m/s).

震源数量	首震源位置(m)	震源间隔 (m)	接收器数量	首接收器位置(m)	接收器间隔(m)	接收器/震源埋藏深度(m)	震源频率(Hz)	接收器采样间隔(s)	接收器采样长度
7	50	100	140	0	5	0	25	0.001	1000

为了构造符合scalar方法的观测系统输入, 我们还需要将抽象的观测系统参数转化为具体的数组:

# source_locations
source_locations = torch.zeros(n_shots, n_sources_per_shot, 2, dtype=torch.long, device=device)
source_locations[..., 1] = source_depth                                         # 二元组的y轴信息 (深度是统一的, 可共同赋值)
source_locations[:, 0, 0] = (torch.arange(n_shots) * d_source + first_source)   # 二元组的x轴信息

# receiver_locations
receiver_locations = torch.zeros(n_shots, n_receivers_per_shot, 2, dtype=torch.long, device=device)
receiver_locations[..., 1] = receiver_depth                                     # 二元组的y轴信息
receiver_locations[:, :, 0] = ((torch.arange(n_receivers_per_shot) * d_receiver + first_receiver).repeat(n_shots, 1))

# source_amplitudes
source_amplitudes = (deepwave.wavelets.ricker(freq, nt, dt, peak_time).repeat(n_shots, n_sources_per_shot, 1).to(device))

震源数组source_locations是三维的, 第一维描述一套地震记录包含几炮, 第二维描述一炮数据包含几个震源 (默认是1), 第三维描述一个震源的位置 (x, y).
这里专门设置第二维并非冗余, 可以理解是与receiver_locations相互对应, 保证数据结构类似.
例如, 基于我们的观测系统, 这里是一个$7\times 1\times 2$的tensor数组:

[tensor([[[ 10,   0]],
         [[ 30,   0]],
         [[ 50,   0]],
         [[ 70,   0]],
         [[ 90,   0]],
         [[110,   0]],
         [[130,   0]]], device='cuda:0')]

接收器数组receiver_locations 是三维的, 第一维描述一套地震记录包含几炮, 第二维描述一炮数据包含几个接收器, 第三维描述一个接收器的位置 (x, y).
例如, 基于我们的观测系统, 这里是一个$7\times 140\times 2$的tensor数组:

tensor([[[  0,   0],
         [  1,   0],
         [  2,   0],
         ...,
         [137,   0],
         [138,   0],
         [139,   0]],

        [[  0,   0],
         [  1,   0],
         [  2,   0],
         ...,
         [137,   0],
         [138,   0],
         [139,   0]],
    
    ...
        
        [[  0,   0],
         [  1,   0],
         [  2,   0],
         ...,
         [137,   0],
         [138,   0],
         [139,   0]]], device='cuda:0')

这里使用了.repeat()方法, 这个方法经常用于Tensor数据的重复叠加操作.
简单来说, .repeat()所操作的对象将被认为是分块矩阵中的子矩阵, 然后将这个矩阵按照repeat中的方法进行排列.
例子如下图:

deepwave.wavelets.ricker显然是deepwave内置的雷克子波生成函数, 其输入参数依次为:

1. 震源频率
2. 接收器采样次数
3. 接收器采样间隔
4. 雷克子波波长

调用参数本身没什么难度, 但额外要注意的地方在于, scalar对于震源波信息的接收也是基于一种数组 (代码中的source_amplitudes)
其基本结构类似于震源数组source_locations, 只不过把原本震源位置的坐标信息换成了震源释放的全采样区间的波信息.
例如, 基于我们的观测系统, 这里是一个$7\times 1\times 1000$的tensor数组:

tensor([[[-2.3323e-13, -5.5781e-13, -1.3173e-12,  ..., -0.0000e+00,
          -0.0000e+00, -0.0000e+00]],

        [[-2.3323e-13, -5.5781e-13, -1.3173e-12,  ..., -0.0000e+00,
          -0.0000e+00, -0.0000e+00]],

        [[-2.3323e-13, -5.5781e-13, -1.3173e-12,  ..., -0.0000e+00,
          -0.0000e+00, -0.0000e+00]],

        ...,

        [[-2.3323e-13, -5.5781e-13, -1.3173e-12,  ..., -0.0000e+00,
          -0.0000e+00, -0.0000e+00]],

        [[-2.3323e-13, -5.5781e-13, -1.3173e-12,  ..., -0.0000e+00,
          -0.0000e+00, -0.0000e+00]],

        [[-2.3323e-13, -5.5781e-13, -1.3173e-12,  ..., -0.0000e+00,
          -0.0000e+00, -0.0000e+00]]], device='cuda:0')

其中每个长度1000的数组都如下图:

3.2 调用scalar来正演

out = deepwave.scalar(v, dx, dt, source_amplitudes=source_amplitudes,
             source_locations=source_locations,
             receiver_locations=receiver_locations,
             accuracy=8,
             pml_freq=freq)

没有复杂的空间有限差分法的细节与迭代, 直接一个函数解决所有问题.
但是也要注意两个参数, 第一是accuracy, 它是空间有限差分的阶数, 其并不是一个可随意填写的变量, 其值仅可于{2,4,6,8}中选择.

第二是pml_freq, 这个参数是可选的, 但建议使用它, 因为它允许您指定 PML 的主频率, 这有助于最大限度地减少边缘反射.
最后, out返回了7个Tensor对象, 这与我们设置的炮集数量并无关系, 仅是巧合.
通过我的观察, 似乎前2个是波场快照的最后时刻. 而中间4个是对应的PML边界图, 它们的大小均为$7\times 180\times 180$.
这里的$180$是原尺寸加上PML边界的大小, 即$140+20+20$.

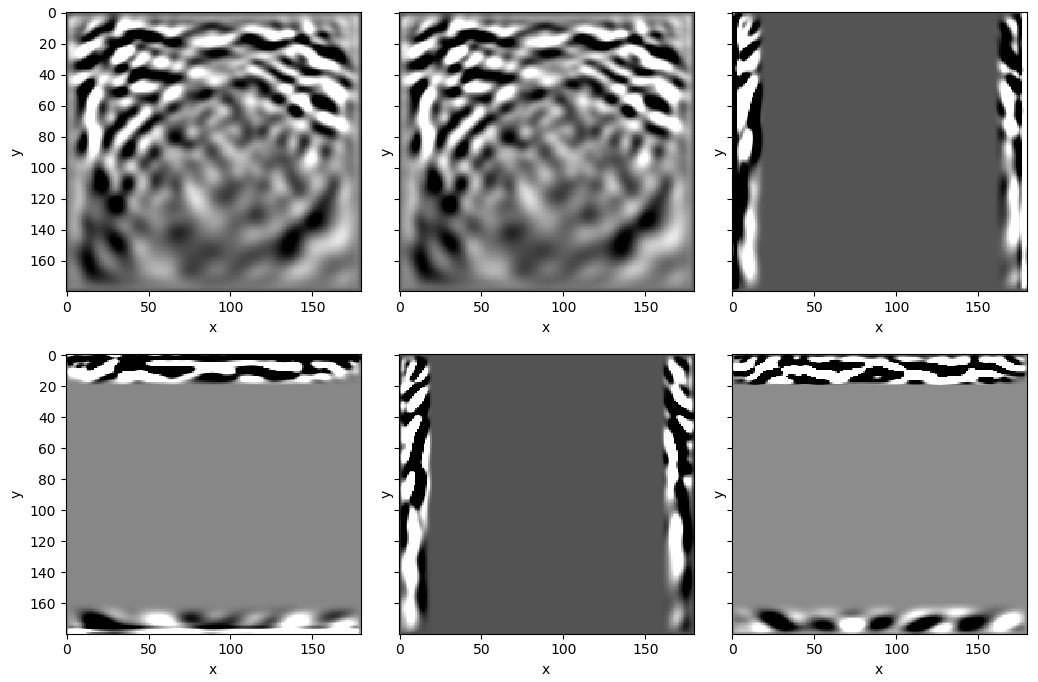
而数组的最后一个Tensor就是我们需要的接收器得到的地震记录图像, 通过下述代码即可输出:

# Plot
receiver_amplitudes = out[-1]
vmin, vmax = torch.quantile(receiver_amplitudes[0], torch.tensor([0.05, 0.95]).to(device))
plt.imshow(receiver_amplitudes[3].cpu().T, aspect='auto', cmap='gray', vmin=vmin, vmax=vmax)
plt.tight_layout()
plt.show()

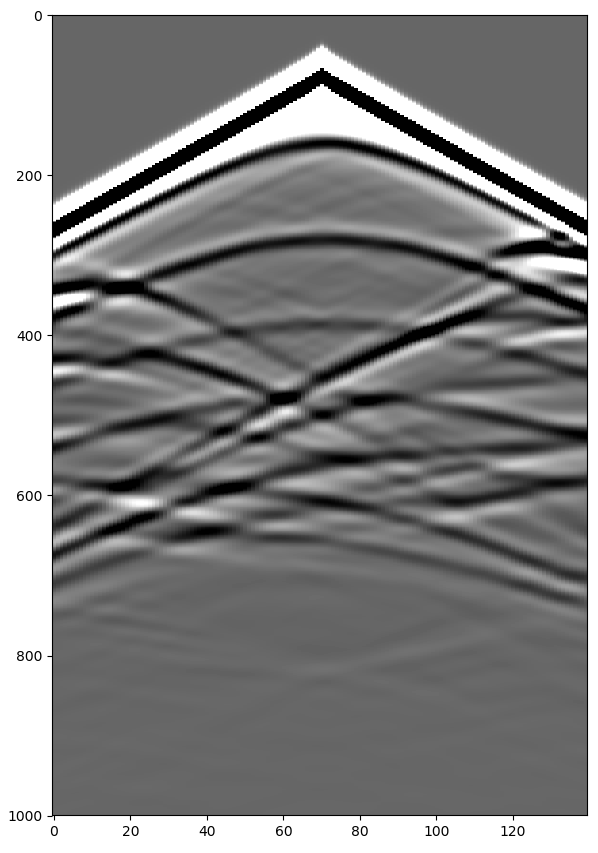
值得一提的是, 在地震记录显示任务中我们使用了torch.quantile()函数. 这是一个非常方便的函数, 首先此方法将对象Tensor数据内数据从小到大排序, 然后通过设置一个范围于[0, 1]的位置参数p来定位排序后的位置, 并返回对应位置最近的值.
以本代码使用为例, vmin, vmax = torch.quantile(receiver_amplitudes[0], torch.tensor([0.05, 0.95]), 这里的第一个目标对象是地震记录receiver_amplitudes[0], quantile会将这个二维的地震记录压缩为一维并按照值从小到大排序. 第二个目标对象是torch.tensor([0.05, 0.95], 它提供了两个位置0.05和0.95. 基于这俩位置, quantile将依次返回排序数组中从左到右位于5%与95%位置的数值. 这俩数值分别作为vmin与vmax.

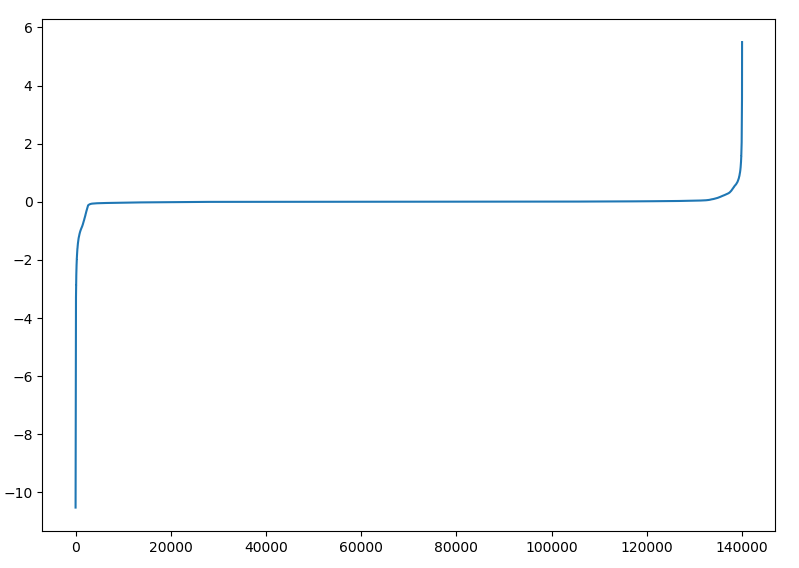
所以为什么要这么做, 我直接选地震记录中最大值作为vmax, 最小值作为vmin不好吗? 实际上, 地震记录中所有数值排序后的变化曲线并非线性, 而是一个中间缓两头极陡的曲线 (见下). 其原因在于地震记录中初至/直达波部分的信号要远高于其下方的反射波与衍射波信号, 在现场数据中, 这种情况将更严重. 如果我们只是单纯地将最大信号设为显示的max, 那么我们将无法在图中观察到下方的反射信息. 因此为取巧, 可利用quantile仅选前5%和后5%.

经过相对草率的测试, 连续执行100次正演 (包括所有震源) 的时间开销大概在13.4左右, 1000次正演的时间大概在125.8s左右, 10000次大概在1249.76s左右.
而CPU并行执行的话, 采用多进程 (Py没有严格意义上的多线程), 一次包括所有震源的正演时间稳定在1.15s左右, 因此100次正演时间会稳定在115s左右, 1000次就是1150s. 当然我为什么要说是相对草率的测试呢, 因为我使用CPU正演代码的观测系统会小些, 仅有$70\times 70$, 但是就算如此, CPU的运行时间也是GPU的十倍.

以OpenFWI的开源数据为例, Fault类数据有48000个, 我们用CPU对每个数据进行正演 (7炮) 将花费15.3h, 而GPU只需要1.67h (实际上不需要这么多, 因为OpenFWI速度模型的$70\times 70$的观测系统是小于本文实验的观测系统).

注: 博主使用的GPU是RTX 3060, CPU是i5-13600K

4. Deepwave的全波形反演 (FWI)

我们在之前正演结果的基础上进一步进行反演任务:
首先, 最小化任务必要的条件是初始解和拟合的目标.

observed_data = out[-1]
v_true = v
v_init = (torch.tensor(1/gaussian_filter(1/v_true.detach().cpu().numpy(), 40)).to(device))      # 对真实模型进行平滑以创建初始模型
v = v_init.clone()
v.requires_grad_()  # v_init, v_true都不会被追踪, 仅v会

这里利用高斯滤波gaussian_filter函数从真实的速度模型出发构造一个初始速度模型v_init, 同时设置了主要的工作变量v用于后续迭代 (将其设置梯度追踪)

# 使用与 PyTorch 中用于训练典型神经网络的代码非常相似的代码来实现.
# 唯一显着的区别是，我们使用更大的学习率 (1e9) 将梯度值提升到一个范围
optimiser = torch.optim.SGD([v], lr=1e9, momentum=0.9)
loss_fn = torch.nn.MSELoss()

# Run optimisation/inversion
n_epochs = 50

for epoch in range(n_epochs):
    optimiser.zero_grad()
    # 在当前速度模型的基础上正演
    out = deepwave.scalar(
        v, dx, dt,
        source_amplitudes=source_amplitudes,
        source_locations=source_locations,
        receiver_locations=receiver_locations,
        pml_freq=freq,
    )
    loss = loss_fn(out[-1], observed_data)
    print(out[-1].grad_fn)# <DivBackward0 object at 0x000002B4546DD898>
    print(loss.grad_fn)# <MseLossBackward0 object at 0x000002B4546DD898>
    loss.backward()
    
    torch.nn.utils.clip_grad_value_(
        v,
        torch.quantile(v.grad.detach().abs(), 0.98)
    )
    optimiser.step()

如果对本博客的第2节了解了的话, 这里的操作可以说是水到渠成.
迭代区域外, 我们声明了SGD优化器optimiser, 并将其与被追踪变量v所绑定, 这将帮助优化器后续查询v的梯度与更新v.
迭代区域内, 首先通过.zero_grad()清理梯度, 避免与上回合的梯度累计.
然后建立对于当前追踪变量v的运算链, 如下图所示 (最小化的运算链都是类似的):

Deepwave给我们最大的帮助out[-1]到v的这段链路的梯度的自动计算.
然后, loss触发backward之后, 链路上所有被追踪的变量 (requires_grad = True) 都将更新梯度, 这里主要是更新v的梯度.

clip_grad_value是非常经典的梯度裁剪操作 (剪裁到梯度值的第98百分位数), 以避免在少数几个点上 (如波源周围) 发生非常大的变化.
注意, 我们不希望此处裁剪操作被追踪, 因此我们在带入梯度值时使用了.detach(), 以取消梯度追踪.

最后, optimiser使用step()以触发优化器利用v的梯度来更新v自身.

值得一提的是, 一些DL-FWI为了提高自身方法的物理意义, 它们也会利用速度模型在数值反演过程中的梯度. 在这种场景下, 调用这些梯度就是非常简单的事情了 (直接返回最后轮迭代的v.grad即可)

相关论文: Adjoint-Driven Deep-Learning Seismic Full-Waveform Inversion

展示代码及结果如下:

# Plot
vmin = v_true.min()
vmax = v_true.max()
_, ax = plt.subplots(3, figsize=(10.5, 10.5), sharex=True, sharey=True)
ax[0].imshow(v_init.cpu().T, aspect='auto', vmin=vmin, vmax=vmax)
ax[0].set_title("Initial")
ax[1].imshow(v.detach().cpu().T, aspect='auto', vmin=vmin, vmax=vmax)
ax[1].set_title("Out")
ax[2].imshow(v_true.cpu().T, aspect='auto', vmin=vmin, vmax=vmax)
ax[2].set_title("True")
plt.tight_layout()
plt.savefig('openfwi_fwi.png')
plt.show()

可以发现, 重建速度模型的前几层还算清醒, 但是深层就不尽人意了.

Deepwave作者给出了解释:

1. 反演过程中特定单元 (特定迭代epoch内速度可能超过目标速度值范围) 中的速度值有可能过大或过小, 从而导致稳定性问题, 这是由于在震源和接收器附近梯度值过大, 优化器因此在那里采取了较大的步长.
2. 第二个问题是经典的周期跳跃, 即正演的结果与观察目标的偏移超过半个波长, 这个时候能取得一个局部最小, 但是显然偏离正确解.
   下面作者对代码进行了一些改进来完善这些目标.

5. Deepwave的反演改进

5.1 限制速度范围

解决极端速度值问题的一种方法是将速度限制在所需的范围内, 当每轮最小化后的速度超过一定阈值我们就将其规范到预设范围内.
因为PyTorch可以让我们将运算符串联起来, 并通过它们自动反向传播以计算梯度, 所以我们可以使用一个函数来生成我们的速度模型.
此处作者提供了一种方便而稳健的方法来限制模型中的速度范围, 我们可以将速度模型定义为一个对象:

class Model(torch.nn.Module):
    def __init__(self, initial, min_vel, max_vel):
        super().__init__()
        self.min_vel = min_vel
        self.max_vel = max_vel
        self.model = torch.nn.Parameter(
            torch.logit((initial - min_vel) /
                        (max_vel - min_vel))
        )

    def forward(self):
        return (torch.sigmoid(self.model) *
                (self.max_vel - self.min_vel) +
                self.min_vel)

其中包含一个与模型大小相同的张量 (代码中的self.model), 这个张量在声明的时候就按照我们预设范围进行 “归一化 + logit”.
当我们调用该对象的 forward 方法时, 它会返回对存储的张量进行 “sigmoid + 逆归一化” 运算后的结果.
因为logit与sigmoid互为反函数, 因此这个操作对于范围正常的速度模型self.model, “sigmoid + 逆归一化” 后数值不会发生改变.

我们假设范围正常的速度模型在 “归一化 + logit” 后的正常速度范围是[a, b]. 如果被优化器改动后, self.model可能出现小于a或者大于b的速度, 即速度模型因为过大的步长导致超过预设速度范围. 但是不用担心, forward 方法中的 “sigmoid” 运算总能将这个范围约束在[0, 1]的归一化范围内, 因此再逆归一化后, 我们的速度范围依旧在预设速度范围内.

总得来说, 这个操作延长的运算链: 额外通过一个渐近于"y = 1" 与 "y = 0"的函数来限制速度范围, 最终通过逆归一化还原到正常速度范围.

(下面是logit函数)

5.2 减少地震记录底部伪影

这是一个较为泛用的处理手段, 往往来说它可以归结为正演结果的数据整理.
cosine_taper_end是deepwave内部封装的函数, 读者们想使用的话直接在代码内部通过deepwave.common.cosine_taper_end调用即可.
其内部代码及参数说明如下:

def cosine_taper_end(signal: Tensor, n_taper: int) -> Tensor:
    """Tapers the end of the final dimension of a Tensor using a cosine.

    A half period, shifted and scaled to taper from 1 to 0, is used.

    Args:
        signal:
            The Tensor that will have its final dimension tapered.
        n_taper:
            The length of the cosine taper, in number of samples.

    Returns:
        The tapered signal.
    """
    taper = torch.ones(signal.shape[-1],
                       dtype=signal.dtype,
                       device=signal.device)
    taper[len(taper) - n_taper:] = (torch.cos(
        torch.arange(1, n_taper + 1, device=signal.device) /
        n_taper * math.pi) + 1).to(signal.dtype) / 2
    return signal * taper

signal是每次迭代时正演输出的地震记录, 在我们的观测系统下, 它是一个$7\times 140\times 1000$的tensor数组.
n_taper表明cosine taper的长度 (以samples样本)

通过简单阅读代码可以发现, 这里构造了一个taper数组, 这个数组长度与接收器的采样长度有关, 例如这里就是一个长度为1000的数组.
数组主要值为1.0, 但是在taper后半段的长度为n_taper的部分替换为一个逐步下降的一个余弦曲线 [0, π] 部分.

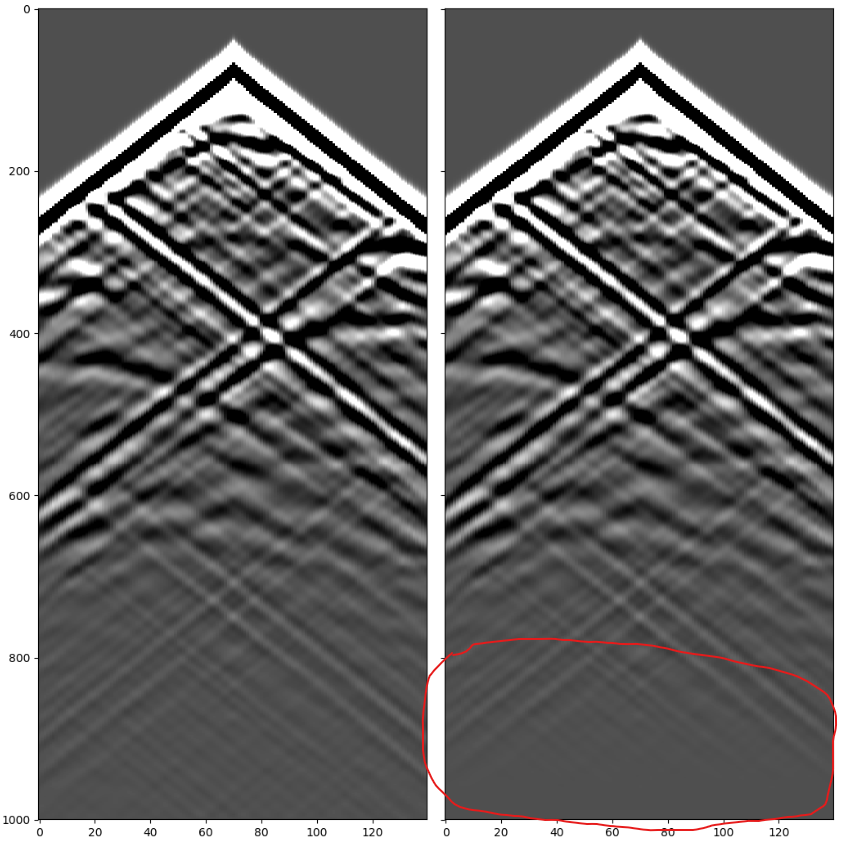
上图是我们将n_taper设置为200, 然后在反演中途观测到的地震记录. 可以发现下侧的确有一定程度的非线性削弱.
由于波的叠加以及边界处理不当, 对于某些地震记录会在底部出现非常严重的伪影, 这时这种尾部削弱就很有意义了.

5.3 缓解周期跳跃

周期跳跃是传统全波形反演的一个非常典型的缺陷.
它在两个数据集之间的相位差异大于半个波长时发生.
一种常见的补救方法是最初只使用数据中的低频, 然后逐渐增加使用的最高频率.
作者用一种简单的方法来实现这一点, 首先从早期迭代的 10 Hz 初始截止频率逐步提高到最后迭代的 30 Hz.
为了保持示例的简单, 作者将把频率滤波器直接应用于正演的输出.
在更复杂的实施过程中可能会对震源的振幅直接滤波 (直接采用较低Hz的震源?), 因为较低频率的震源可以让我们使用更大的网格间距, 从而降低计算成本.

为了应用频率滤波器, 我们使用一连串的二阶部件, 利用 torchaudio 的 biquad 函数和 scipy 的 butter 实现一个 六阶巴特沃斯滤波器

巴特沃斯滤波器比一般的滤波器来说, 响应曲线会更大限度平坦, 没有起伏

其示例代码如下:

for cutoff_freq in [10, 15, 20, 25, 30]:

    sos = butter(6, cutoff_freq, fs=1/dt, output='sos')
    sos = [torch.tensor(sosi).to(observed_data.dtype).to(device)
           for sosi in sos]

    def filt(x):
        return biquad(biquad(biquad(x, *sos[0]), *sos[1]), *sos[2])

    observed_data_filt = filt(observed_data)

# ...下述略...

因为我并不做信号处理, 有些滤波处理细节不是很清楚, 我只能解释表象.
butter用于返回N阶的巴特沃斯滤波器系数, 我们这里N=6. 然后输入参数分别是截取的频率 (cutoff_freq) 与数字系统的采样频率 (1/dt).
返回值是一个$3\times N$的Numpy矩阵, 于是我们依次将每个值转化为Tensor, 然后存储到$3$个list对象中.
然后作者叠加使用了3次biquad滤波器, 每次滤波器都馈入7个参数, 第一个是输入图像, 后六个是来自巴特沃斯滤波器系数的某一行. 这里的叠加输入刚好使用了前三行.

简单来说, 分别通过低通滤波器将地震观测记录依次限制在10, 15, 20, 25, 30Hz以下, 得到5个副本.
然后依次利用每个副本来做最小化.

5.4 主要代码:

紧接着第3节的正演结果, 我们补充如下代码

def taper(x):
    return deepwave.common.cosine_taper_end(x, 100)

class Model(torch.nn.Module):
    def __init__(self, initial, min_vel, max_vel):
        super().__init__()
        self.min_vel = min_vel
        self.max_vel = max_vel
        self.model = torch.nn.Parameter(
            torch.logit((initial - min_vel) /
                        (max_vel - min_vel))
        )

    def forward(self):
        return (torch.sigmoid(self.model) *
                (self.max_vel - self.min_vel) +
                self.min_vel)
                
observed_data = out[-1]
observed_data = taper(observed_data)

v_true = v
v_init = (torch.tensor(1/gaussian_filter(1/v_true.detach().cpu().numpy(), 40)).to(device))
v = v_init.clone()
v.requires_grad_()
loss_fn = torch.nn.MSELoss()
n_epochs = 2

model = Model(v_init, 1500, 4500).to(device)

for cutoff_freq in [10, 15, 20, 25, 30]:
sos = butter(6, cutoff_freq, fs=1/dt, output='sos')
    sos = [torch.tensor(sosi).to(observed_data.dtype).to(device) for sosi in sos]

    def filt(x):
        return biquad(biquad(biquad(x, *sos[0]), *sos[1]), *sos[2])

    observed_data_filt = filt(observed_data)
    optimiser = torch.optim.LBFGS(model.parameters(), line_search_fn='strong_wolfe')

    for epoch in range(n_epochs):
        def closure():
            optimiser.zero_grad()
            v = model()
            out = scalar(
                v, dx, dt,
                source_amplitudes=source_amplitudes,
                source_locations=source_locations,
                receiver_locations=receiver_locations,
                max_vel=4500,
                pml_freq=freq,
                time_pad_frac=0.2,
            )
            out_filt = filt(taper(out[-1]))
            loss = 1e6*loss_fn(out_filt, observed_data_filt)
            loss.backward()
            return loss

        optimiser.step(closure)
        
v = model()

关于这个代码, 仍然有一些留意的地方.

1. 首先是作者在这里并未采用SGD, 而是一种名为L-BFGS的下降策略, 它是BFGS的一种轻量化版本 (Limited-memory BFGS).

L-BFGS的基本思想就是通过存储前m次迭代的少量数据来替代前一次的矩阵, 从而大大减少数据的存储空间. 而BFGS就是使用之前的所有梯度.

3. 这里L-BFGS的调用显得怪怪的是因为它在Pytorch中的使用与其他优化器有些不同, 因为它需要把计算链的说明 (forward一个速度模型 + 正演 + MSE损失计算) 以及梯度更新操作 (backward) 全部放在一个固定的函数操作 (本例为函数closure) 中. 然后在优化器执行step操作时传入这个函数的地址.
4. 可以发现L-BFGS的声明中使用了函数.parameters(). 因为当你声明了一个类, 同时这个类中具备Parameter对象, 那么调用类中默认自带的parameters()即可以快速利用的类内的Parameter对象. 此外, Parameter对象可以直接作为优化器的输入参数, 而Tensor的话在输入时需要外套一个[ ].
5. 与 LBFGS 相关的另一个变化是对损失进行了缩放 (本例中为 1e6), 这是因为当数值小于阈值时, LBFGS 优化器就会停止工作. 自然, 我们可以改变 LBFGS 的阈值, 但是如此改动更简单. 如果不改变缩放比例, 而是改用使用梯度值更新模型的优化器 (如梯度下降法)，那么就应该按照这个缩放因子降低优化器的学习率, 这样更新的大小就不会改变. 因为缩放损失会缩放梯度, 所以缩放比例会被学习率的降低抵消.
6. 请注意, 每次改变频率时, 我们都会创建一个新的优化器. 因为在发生如此大的变化后仍继续使用同一个优化器的话, 它可能会让一些会考虑先前迭代历史的优化器感到困惑. 刚好LBFGS就是这样的一种优化器.
7. scalar带入了一个新的参数time_pad_frac, 其解释如下:

time_pad_frac - 一个浮点数, 指定在重采样前添加到震源振幅和接收振幅 (如果存在) 上的零填充量, 如果由于 CFL 条件导致重采样, 则在重采样后移除零填充量, 占其长度的一部分. 这可能有助于减少缠绕 (wraparound) 伪影. 0.1 表示使用时间采样数 10%的零填充. 默认值为 0.0.

最后运行效果如下图:

这比第4节所展示的效果要好很多, 深层的边界范围清晰了许多. 但是深层速度与真实速度还存在一定程度的差异.
当然, 我们不可能以这些简单的处理挑战传统的数值迭代FWI历经如此十多年的发展, 例如, 数值迭代FWI还可以通过各种正则来实现更好的效果, 以及更多我所不知的优化策略.
但是我相信, 对于做DL-FWI的人来说, 这将是非常有物理先验认知启发的过程.

最后, 从迭代次数角度来看, 每个频率副本都仅迭代2次, 因此总的epoch只有10次.
这要低于第4节我们采用SGD设置的50次epoch, 但是实际运行时间却要长很多.
一方面, 这直观地告诉了我们不同优化器之间固然是有运行时间上的差异, 另一方面, 从结果的角度来看, 采用合理的方法 (逐步迭代不同频率的地震记录和限制速度范围) 也能在有限的迭代中取得更好的成果.

原文地址：https://blog.csdn.net/qq_30016869/article/details/138850281

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！