吴恩达2022机器学习专项课程C2W2:实验Relu激活函数
目录
代码修改
1.Activation
(1)需要添加代码from tensorflow.keras import activations。然后在from tensorflow.keras.layers import Dense, LeakyReLU后添加Activation。

(2)然后在如下代码中这样修改。原有的写法已被弃用,这是新的写法。

2.Dense
(1)注释代码是原有代码。我们需要改成注释下方的写法。因为现在的TF版本中,Dense层的weights参数不被直接接受。需要先bulid初始化层的权重,这里的None不确定样本数量,用于占位,1表示样本的特征为1个。

(2)同理,这里也要改。

3.代码顺序
(1)这是错误的顺序,model未定义。

(2)这是正确的顺序,需要把使用model的预测放在构建model之后。

新的内容
1.总结上节课内容
(1)神经元的激活值awareness不在是0或1,是任意非负数。而Sigmoid函数是一种常用于二分类问题的激活函数,它能够输出一个介于0和1之间的值,适合表示概率或开关状态。 因此需要ReLU激活函数,它在输入大于0时提供线性输出,这意味着输出与输入成正比,提供了一个平滑的连续变化。此外,它还有一个"关闭"范围,其中输出为零。 这是ReLU的一个关键特性,即当输入小于0时,ReLU的输出为0,这个特性被称为"关闭",也使它成为了非线性激活函数。

2.展示ReLU激活函数的好处
(1)我们需要构建神经网络,它模拟一个分段线性的目标函数,目的是理解ReLU如何开启和关闭函数的。这里神经网络的隐藏层都使用ReLU激活函数。

(2)左图中,神经元1和神经元2的参数已经设置好,神经元0的参数也已经固定。神经元0负责第一段的走势,神经元2负责第二段的走势,神经元3负责第三段的走势。由于每个神经元的参数都是合适的,因此横轴x代入神经元预测出的每个分段的走势,都符合目标(分段线性函数)走势。

(3)然后再看右图,右图的两个线条,蓝色和粉色,是分别展示了每个神经元的线性激活函数的输出z和ReLU激活函数的输出a。
- 第一个神经元使用ReLU的输出走势在x[0,1]区间,之后的输出都为0,符合左图的第一段,即神经元0不会影响x大于1之后的走势。
- 第二个神经元使用ReLU的输出走势在x大于1之后,之前的输出都为0,符合左图的第二段,即神经元1不会影响x小于1之前的走势。
- 第三个神经元使用ReLU的输出走势在x大于2之后,之前的输出都为0,符合左图的第三段,即神经元2不会影响x小于2之前的走势。

3.结论
如果神经元没有激活函数,或使用不具备这种特性的激活函数,则每个神经元的走势都会互相影响,无法达到拼接的效果。因此,ReLU激活函数的“关闭”(输出为0),使模型能够拼接线性段来模拟复杂的非线性函数。
代码案例一
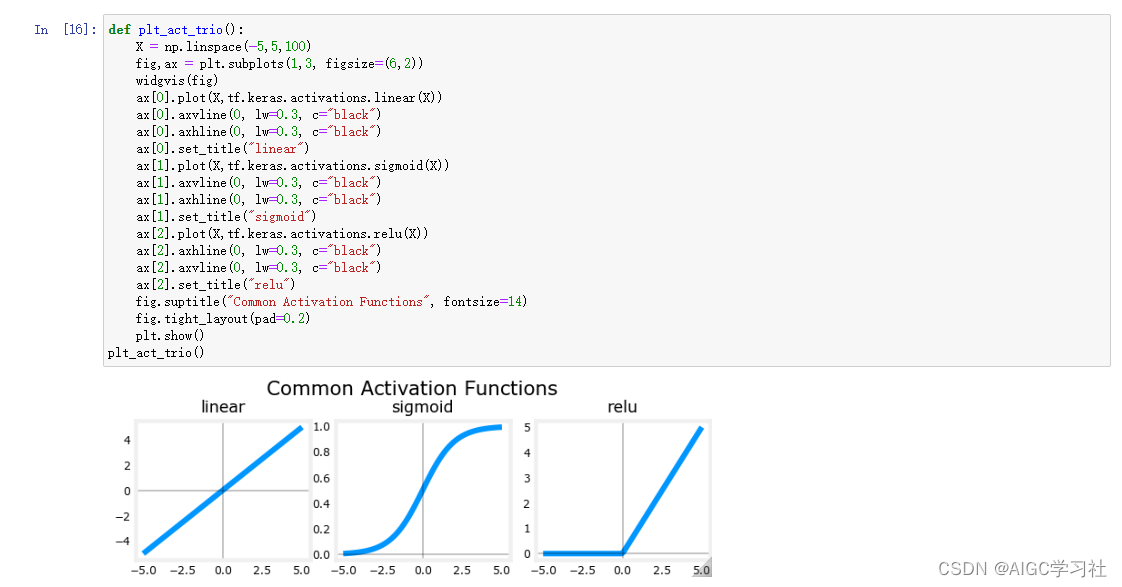
(1)首先展示3种激活函数的输入和输出的关系。
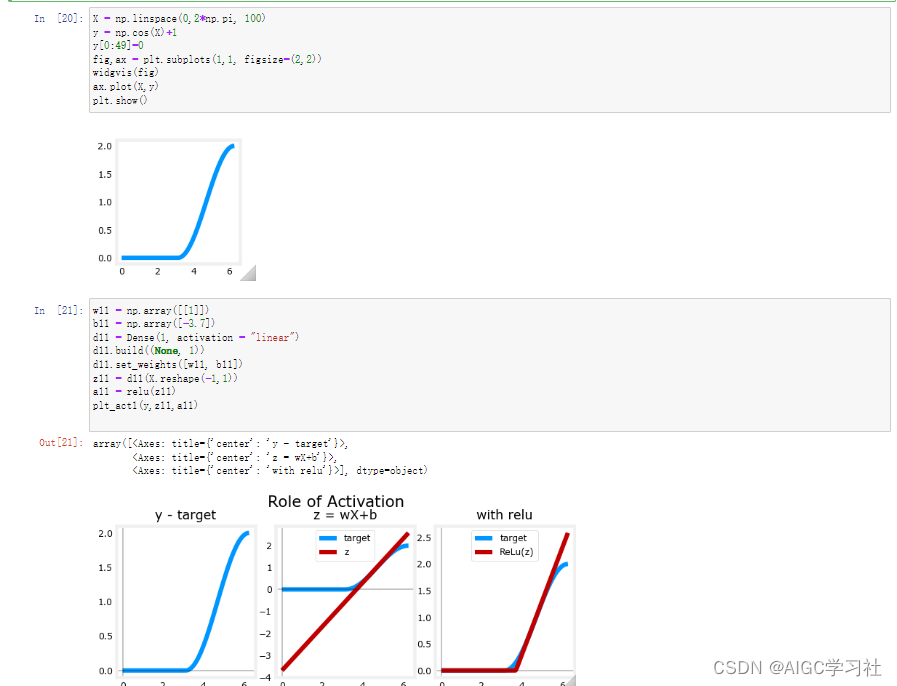
(2)然后自定义一个数据集,并绘制数据集。

(3)先设置一个神经层d10,神经元为1个,激活函数为linear,然后计算神经层的输出z10(wx+b),在使用ReLU得出层激活值a10。

(4)左边的图是数据集,中间的图表示使用数据集X的情况下,线性激活的表现,能够看到无法拟合数据集的输出。最右边的图是使用ReLU激活计算的值,能够较好的拟合数据集的输出。

(4)下面的内容和上面也是一个过程,只是更换一下数据集的内容。
(5)小结:整体过程就是先自定义一个数据集,然后绘制出来。在把数据集中的X代入到线性激活和ReLU激活,分别看看这两个激活函数计算出的预测值,是否匹配数据集里的目标变量y。在这个案例中,线性激活不匹配,而ReLU匹配。
代码案例二
1.构建数据集
(1)左图是新建的数据集,右侧是ReLU的预测值以及数据集,直观地看到神经网络较好的拟合了数据集。

(2)这是新建数据集中的x。

(3)这段是单独绘制的,实现的功能和上面的一致。

2.构建模型
(1)构建3个层,分别为d10,d11,Dense。两个Activation是激活函数层,这里的Activation设置为ReLU激活函数,也就是d10的激活值用于ReLU计算并输出,然后d11的激活值用于ReLU计算并输出。而模型的输出层,是线性激活,也就是最后一个Dense。

(2)可以看到,如果按上述方法构建神经网络,神经网络的对于输入向量x,预测都为1,无法匹配目标变量。

(3)如果按这种方式构建,两个层,每层一个神经元,则神经网络的预测都为0.37,也无法匹配目标变量。


(4)获取该神经网络的参数,由于我们没有手动设置参数,因此在传入输入向量x之后,这些参数都是神经网络自动初始化的,第一层参数为w=-0.14,b=0。第二层的参数为w=0.9,b=0.37。

(5)手动设置层的参数,继续训练,然后重置第2层的参数。

(6)红色线条表示伸进网络的预测,由于第一层是ReLU,此时w为负数,b为正数,因此z越来越小,ReLU的激活值越来越小,等到z为负数,ReLU的激活值就都为0,而第二层是线性激活,权重为1,偏置为0,因此第二层等于原封不动的把第一层的激活输出。
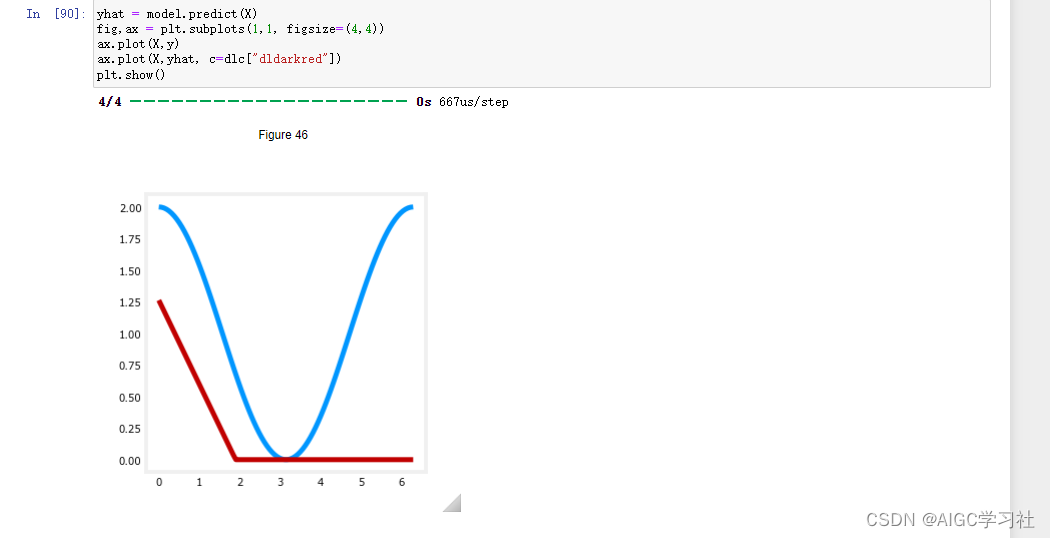
(7)小结:通过手动设置神经网络的权重和偏置,可以控制神经网络的输出趋势。在本例中,通过设置特定的w,b使得神经网络的输出呈现出 ReLU 函数的趋势。
2D
1.构建数据集
(1)导入库

(2)编写绘制图的函数
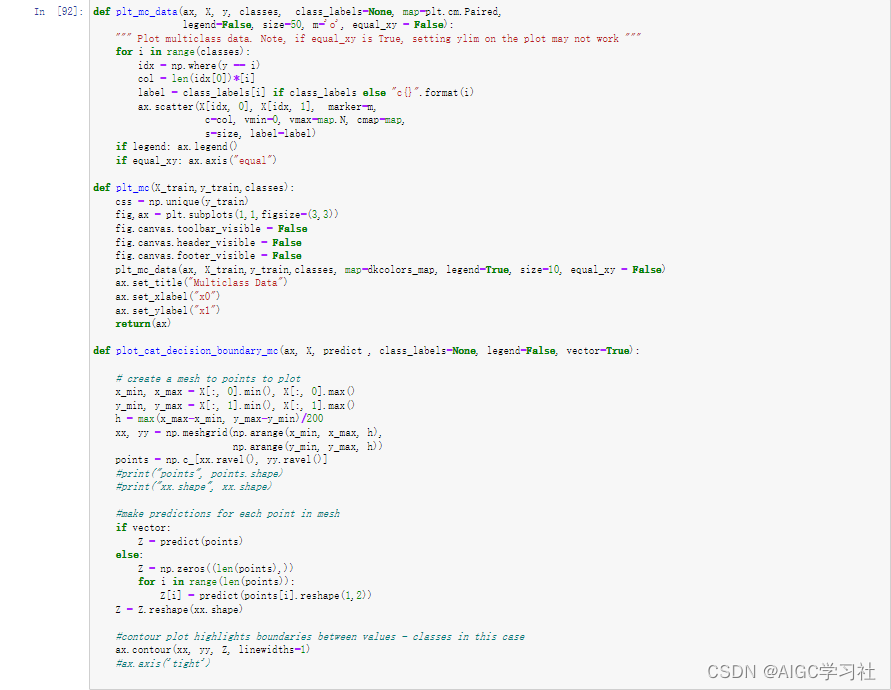
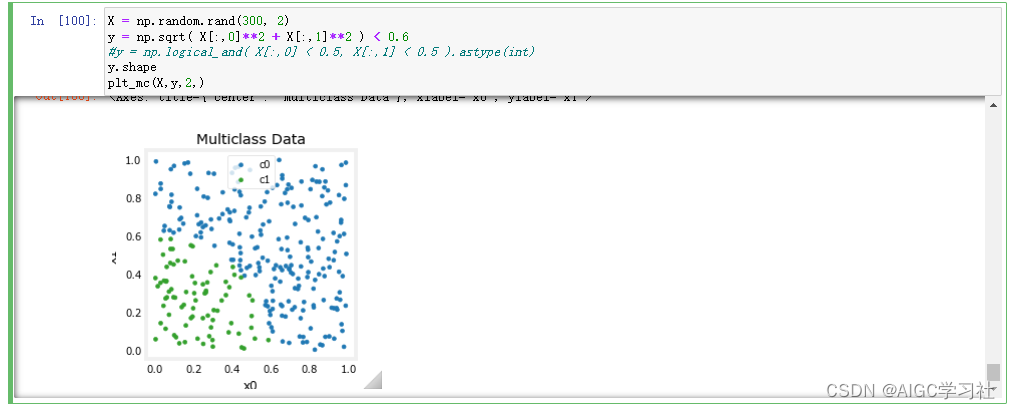
(3)构建数据集并生成图,X有300个训练样本,每个样本2个特征,图片的横轴纵轴分别对应2个特征的值,使用sqrt计算2个特征,小于0.6为true对应蓝色,大于等于0.6对应false,对应绿色。
2.模型预测
(1)构建并训练模型。

(2)使用模型预测,大于0.5为true,对应蓝色,小于0.5为false,对应绿色。
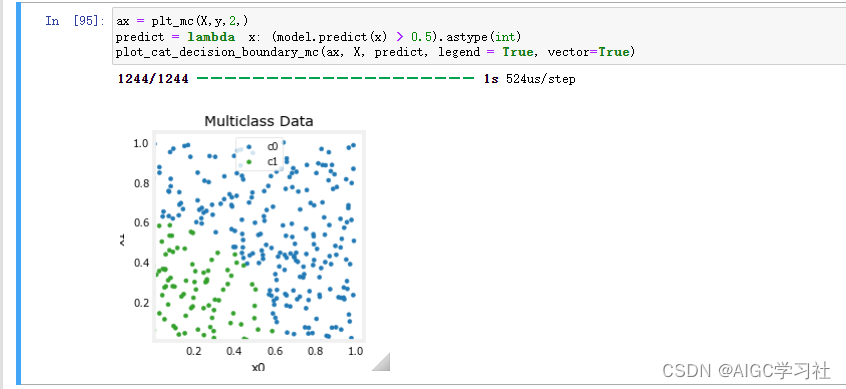
(3)小结:通过比较模型预测的决策边界和实际数据的分布,可以直观地看到模型的分类效果和准确性。
3.扩展
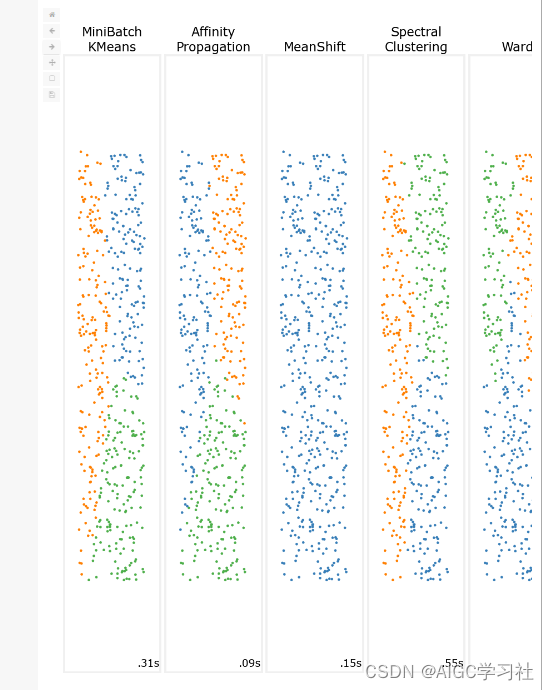
下面代码对多个聚类算法在同一数据集上的表现进行了可视化,展示了不同算法的聚类效果和运行时间。这对比有助于理解不同算法的优缺点及其在不同类型数据上的性能。(聚类算法是无监督学习部分的,我不太清楚此处放这段代码的目的,如果有大佬可以分析一波)
import time
import warnings
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets, mixture
from sklearn.neighbors import kneighbors_graph
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
np.random.seed(0)
# ============
# Generate datasets. We choose the size big enough to see the scalability
# of the algorithms, but not too big to avoid too long running times
# ============
n_samples = 500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None
# Anisotropicly distributed data
random_state = 170
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)
# blobs with varied variances
varied = datasets.make_blobs(
n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)
# ============
# Set up cluster parameters
# ============
plt.figure(figsize=(9 * 2 + 3, 13))
plt.subplots_adjust(
left=0.02, right=0.98, bottom=0.001, top=0.95, wspace=0.05, hspace=0.01
)
plot_num = 1
default_base = {
"quantile": 0.3,
"eps": 0.3,
"damping": 0.9,
"preference": -200,
"n_neighbors": 3,
"n_clusters": 3,
"min_samples": 7,
"xi": 0.05,
"min_cluster_size": 0.1,
}
datasets = [
(
noisy_circles,
{
"damping": 0.77,
"preference": -240,
"quantile": 0.2,
"n_clusters": 2,
"min_samples": 7,
"xi": 0.08,
},
),
(
noisy_moons,
{
"damping": 0.75,
"preference": -220,
"n_clusters": 2,
"min_samples": 7,
"xi": 0.1,
},
),
(
varied,
{
"eps": 0.18,
"n_neighbors": 2,
"min_samples": 7,
"xi": 0.01,
"min_cluster_size": 0.2,
},
),
(
aniso,
{
"eps": 0.15,
"n_neighbors": 2,
"min_samples": 7,
"xi": 0.1,
"min_cluster_size": 0.2,
},
),
(blobs, {"min_samples": 7, "xi": 0.1, "min_cluster_size": 0.2}),
(no_structure, {}),
]
datasets = [
(no_structure, {}),
]
for i_dataset, (dataset, algo_params) in enumerate(datasets):
# update parameters with dataset-specific values
params = default_base.copy()
params.update(algo_params)
X, y = dataset
# normalize dataset for easier parameter selection
X = StandardScaler().fit_transform(X)
# estimate bandwidth for mean shift
bandwidth = cluster.estimate_bandwidth(X, quantile=params["quantile"])
# connectivity matrix for structured Ward
connectivity = kneighbors_graph(
X, n_neighbors=params["n_neighbors"], include_self=False
)
# make connectivity symmetric
connectivity = 0.5 * (connectivity + connectivity.T)
# ============
# Create cluster objects
# ============
ms = cluster.MeanShift(bandwidth=bandwidth, bin_seeding=True)
two_means = cluster.MiniBatchKMeans(n_clusters=params["n_clusters"])
ward = cluster.AgglomerativeClustering(
n_clusters=params["n_clusters"], linkage="ward", connectivity=connectivity
)
spectral = cluster.SpectralClustering(
n_clusters=params["n_clusters"],
eigen_solver="arpack",
affinity="nearest_neighbors",
)
dbscan = cluster.DBSCAN(eps=params["eps"])
optics = cluster.OPTICS(
min_samples=params["min_samples"],
xi=params["xi"],
min_cluster_size=params["min_cluster_size"],
)
affinity_propagation = cluster.AffinityPropagation(
damping=params["damping"], preference=params["preference"], random_state=0
)
average_linkage = cluster.AgglomerativeClustering(
linkage="average",
affinity="cityblock",
n_clusters=params["n_clusters"],
connectivity=connectivity,
)
birch = cluster.Birch(n_clusters=params["n_clusters"])
gmm = mixture.GaussianMixture(
n_components=params["n_clusters"], covariance_type="full"
)
clustering_algorithms = (
("MiniBatch\nKMeans", two_means),
("Affinity\nPropagation", affinity_propagation),
("MeanShift", ms),
("Spectral\nClustering", spectral),
("Ward", ward),
("Agglomerative\nClustering", average_linkage),
("DBSCAN", dbscan),
("OPTICS", optics),
("BIRCH", birch),
("Gaussian\nMixture", gmm),
)
for name, algorithm in clustering_algorithms:
t0 = time.time()
# catch warnings related to kneighbors_graph
with warnings.catch_warnings():
warnings.filterwarnings(
"ignore",
message="the number of connected components of the "
+ "connectivity matrix is [0-9]{1,2}"
+ " > 1. Completing it to avoid stopping the tree early.",
category=UserWarning,
)
warnings.filterwarnings(
"ignore",
message="Graph is not fully connected, spectral embedding"
+ " may not work as expected.",
category=UserWarning,
)
print(X.shape,algorithm)
algorithm.fit(X)
t1 = time.time()
if hasattr(algorithm, "labels_"):
y_pred = algorithm.labels_.astype(int)
else:
y_pred = algorithm.predict(X)
plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
colors = np.array(
list(
islice(
cycle(
[
"#377eb8",
"#ff7f00",
"#4daf4a",
"#f781bf",
"#a65628",
"#984ea3",
"#999999",
"#e41a1c",
"#dede00",
]
),
int(max(y_pred) + 1),
)
)
)
# add black color for outliers (if any)
colors = np.append(colors, ["#000000"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("%.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
size=15,
horizontalalignment="right",
)
plot_num += 1
plt.show()
原文地址:https://blog.csdn.net/AIGC_xuexishe/article/details/139122099
免责声明:本站文章内容转载自网络资源,如本站内容侵犯了原著者的合法权益,可联系本站删除。更多内容请关注自学内容网(zxcms.com)!
