稀碎从零算法笔记Day37-LeetCode:所有可能的真二叉树

今天的每日一题，感觉理解的还不够深，有待加深理解

题型：树、分治、递归

链接：894. 所有可能的真二叉树 - 力扣（LeetCode）

来源：LeetCode

题目描述

给你一个整数 n ，请你找出所有可能含 n 个节点的 真二叉树 ，并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。

答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表。

真二叉树 是一类二叉树，树中每个节点恰好有 0 或 2 个子节点。（不一定是完全二叉树）

题目样例

示例 1：

输入：n = 7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

示例 2：

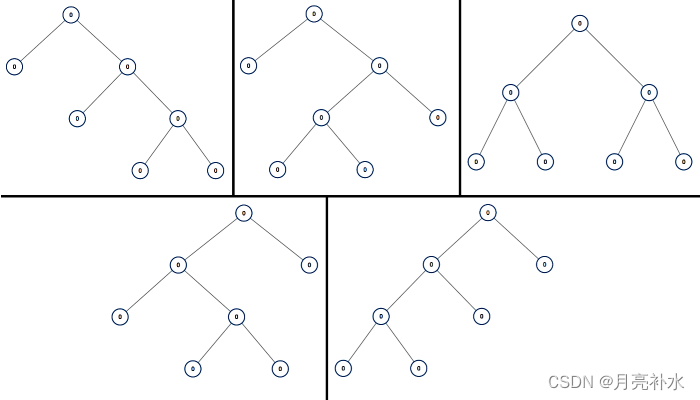
输入：n = 3
输出：[[0,0,0]]

提示：

• 1 <= n <= 20

题目思路

真二叉树的定义能看明白，但如何枚举出来所有的情况不知道该如何实现

看了题解，发现了一种类似二叉树的先序遍历的枚举方法

讲方法之前先说一下真二叉树的特点：真二叉树的节点的度只能是0或2，那么其节点数只能是奇数。然后真二叉树的子树，自然也是真二叉树，那么子树的节点数也是奇数。同时可以知道，真二叉树没将一个叶子节点变成非叶子，那么他就需要长出两个孩子——即多了1个叶子节点。推广可知：真二叉树的叶子数是【n+1/2】——其中n是节点数。

那么我们就知道了真二叉树的节点数。这样我们就能枚举左右子树分别有 i / n - i - 1 个节点的情况。创一个数组leftSon[i] 来表示左子树节点数为 i 的情况，那么对应的rightSon[i] 表示右子树的情况。

C++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //每个节点的出度只能是 0 或者 2 
    // 真二叉树 节点数一定为奇数
    // 返回所有真二叉树的情况
    vector<TreeNode*> allPossibleFBT(int n) {
        vector<TreeNode *> ans;
        if(n % 2 == 0)
            return ans;
        // 只有一个节点 或者左/右子树只有一个节点，此时递归结束
        if(n == 1)
        {
            ans = {new TreeNode(0)};
            return ans;
        }
        // 节点数只能是奇数，左/右子树的节点数也得是奇数个
        for(int i = 1;i < n ; i += 2)
        {
            // 对左/右子树的所有节点个数枚举出来
            vector<TreeNode *>leftSon = allPossibleFBT(i);
            vector<TreeNode *> rightSon = allPossibleFBT(n-1-i);
            for(auto L : leftSon)
            {
                for(auto R : rightSon)
                {
                    ans.emplace_back(new TreeNode(0,L,R));
                    // ans.emplace_back(root);
                }
            }
        }
        return ans;
    }
};

结算页面

原文地址：https://blog.csdn.net/m0_63356844/article/details/137298118

免责声明：本站文章内容转载自网络资源，如本站内容侵犯了原著者的合法权益，可联系本站删除。更多内容请关注自学内容网（zxcms.com）！